1 - Sequence to Sequence Learning with Neural Networks

This part will be done on German to English translations. Sequence to Sequence Learning with Neural Networks Paper

Introduction

The most common sequence-to-sequence (seq2seq) models are encoder-decoder models, which commonly use a recurrent neural network (RNN) to encode the source (input) sentence into a single vector(context vector). The context vector can be regarded as being an abstract representation of the entire input sentence. This vector is then decoded by a second RNN which learns to output the target (output) sentence by generating it one word at a time.

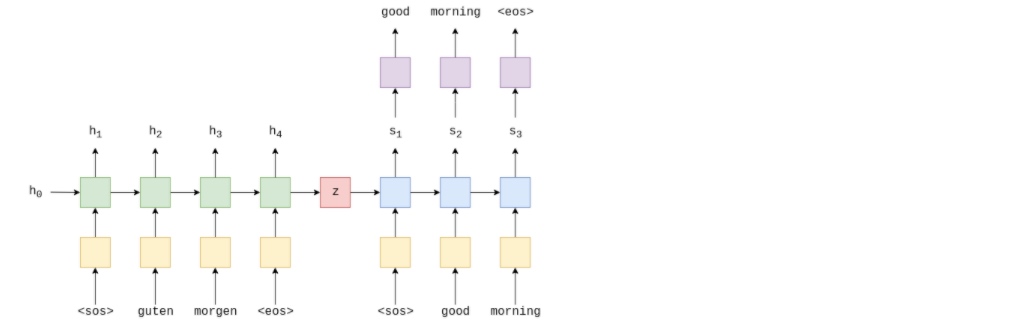
The above image shows an example translation. The input/source sentence, “guten morgen”, is passed through the embedding layer (yellow) and then input into the encoder (green). Need to append a start of sequence () and end of sequence () token to the start and end of sentence, respectively. At each time-step, the input to the encoder RNN is both the embedding, $e$ , of the current word, $e(x_t)$ , as well as the hidden state from the previous time-step, $h_{t-1}$, and the encoder RNN outputs a new hidden state $h_t$. The hidden state can be regarded as a vector representation of the sentence so far. The RNN can be represented as a function of both of $e(x_t)$ and $h_{𝑡−1}$: $$h_t=EncoderRNN(e(x_t),h_{𝑡−1}) $$ RNN could be any recurrent architecture, such as an LSTM (Long Short-Term Memory) or a GRU (Gated Recurrent Unit).

Now have $𝑋=\{𝑥_1,𝑥_2,...,𝑥_𝑇\}$ , where 𝑥1=,𝑥2=guten , etc. The initial hidden state, $ℎ_0$ , is usually either initialized to zeros or a learned parameter.

Once the final word, $𝑥_𝑇$ , has been passed into the RNN via the embedding layer, the final hidden state, $ℎ_𝑇$ , can be used as the context vector, i.e. $ℎ_𝑇=𝑧$ . This is a vector representation of the entire source sentence.

Now have context vector, $𝑧$ , it can start decoding it to get the output/target sentence, “good morning”. Again, append start and end of sequence tokens to the target sentence. At each time-step, the input to the decoder RNN (blue) is the embedding, $𝑑$ , of current word, $𝑑(𝑦_𝑡)$ , as well as the hidden state from the previous time-step, $𝑠_{𝑡−1}$ , where the initial decoder hidden state, $𝑠_0$ , is the context vector, $𝑠_0=𝑧=ℎ_𝑇$ , i.e. the initial decoder hidden state is the final encoder hidden state. Thus, similar to the encoder, we can represent the decoder as: $$ 𝑠_𝑡=DecoderRNN(𝑑(𝑦_𝑡),𝑠_{𝑡−1}) $$ Although the input/source embedding layer, 𝑒 , and the output/target embedding layer, 𝑑 , are both shown in yellow in the diagram they are two different embedding layers with their own parameters.

In the decoder, need to go from the hidden state to an actual word, therefore at each time-step use $𝑠_𝑡$ to predict (by passing it through a Linear layer, shown in purple) what the next word in the sequence, $𝑦̂_𝑡$ . $$𝑦̂_𝑡=𝑓(𝑠_𝑡) $$ The words in the decoder are always generated one after another, with one per time-step. Always use for the first input to the decoder, $𝑦_1$, but for subsequent inputs, $𝑦_𝑡 > 1$ , sometimes will use the actual, ground truth next word in the sequence, $𝑦_𝑡$ and sometimes use the word predicted by our decoder, $𝑦̂_{𝑡−1}$ . This is called teacher forcing.

When training/testing model, always know how many words are in target sentence, so stop generating words once hit that many. During inference it is common to keep generating words until the model outputs an token or after a certain amount of words have been generated.

Once have predicted target sentence, $𝑌̂ =\{𝑦̂_1,𝑦̂_2,...,𝑦̂_𝑇\}$ , compare it against actual target sentence, $𝑌=\{y_1,y_2,...,y_𝑇\}$ , to calculate loss. Then use this loss to update all of the parameters in our model.

Preparing Data

We’ll be coding up the models in PyTorch and using TorchText to help us do all of the pre-processing required. We’ll also be using spaCy to assist in the tokenization of the data.

import torch
import torch.nn as nn
import torch.optim as optim

from torchtext.datasets import TranslationDataset, Multi30k
from torchtext.data import Field, BucketIterator

import spacy
import numpy as np

import random
import math
import time

SEED = 1234

random.seed(SEED)
np.random.seed(SEED)
torch.manual_seed(SEED)
torch.cuda.manual_seed(SEED)
torch.backends.cudnn.deterministic = True

Create the tokenizers. A tokenizer is used to turn a string containing a sentence into a list of individual tokens that make up that string, e.g. “good morning!” becomes [“good”, “morning”, “!”].

spaCy has tokenizer model for each language (“de” for German and “en” for English) which need to be loaded (the models must first be downloaded using the following on the command line:)

!python -m spacy download en
!python -m spacy download de

spacy_de = spacy.load('de')
spacy_en = spacy.load('en')

Create the tokenizer functions. These can be passed to TorchText and will take in the sentence as a string and return the sentence as a list of tokens.

def tokenize_de(text):
    """
    Tokenizes German text from a string into a list of strings (tokens) and reverses it
    
    In the paper, they find it beneficial to reverse the order of the input which they believe "introduces many short term dependencies in the data that make the optimization problem much easier". Therefore, reversing the German sentence after it has been transformed into a list of tokens.
    """
    return [tok.text for tok in spacy_de.tokenizer(text)][::-1]

def tokenize_en(text):
    """
    Tokenizes English text from a string into a list of strings (tokens)
    """
    return [tok.text for tok in spacy_en.tokenizer(text)]

TorchText’s Fields handle how data should be processed. All of the possible arguments are detailed here.

Set the tokenize argument to the correct tokenization function for each, with German being the SRC (source) field and English being the TRG (target) field. The field also appends the “start of sequence” and “end of sequence” tokens via the init_token and eos_token arguments, and converts all words to lowercase.

SRC = Field(tokenize = tokenize_de, 
            init_token = '<sos>', 
            eos_token = '<eos>', 
            lower = True)

TRG = Field(tokenize = tokenize_en, 
            init_token = '<sos>', 
            eos_token = '<eos>', 
            lower = True)

Download and load the train, validation and test data.

The dataset is the Multi30k dataset. This is a dataset with ~30,000 parallel English, German and French sentences, each with ~12 words per sentence.

exts specifies which languages to use as the source and target (source goes first) and fields specifies which field to use for the source and target.

train_data, valid_data, test_data = Multi30k.splits(exts = ('.de', '.en'), fields = (SRC, TRG))

print(f"Number of training examples: {len(train_data.examples)}")
print(f"Number of validation examples: {len(valid_data.examples)}")
print(f"Number of testing examples: {len(test_data.examples)}")
# Number of training examples: 29000
# Number of validation examples: 1014
# Number of testing examples: 1000
print(type(train_data.examples[0]),vars(train_data.examples[0]) # the source sentence is reversed
# <class 'torchtext.data.example.Example'>, {'src': ['.', 'büsche', 'vieler', 'nähe', 'der', 'in', 'freien', 'im', 'sind', 'männer', 'weiße', 'junge', 'zwei'], 'trg': ['two', 'young', ',', 'white', 'males', 'are', 'outside', 'near', 'many', 'bushes', '.']}
print(vars(train_data.examples[0])['src'])
# ['.', 'büsche', 'vieler', 'nähe', 'der', 'in', 'freien', 'im', 'sind', 'männer', 'weiße', 'junge', 'zwei']

Build the vocabulary for the source and target languages. The vocabulary is used to associate each unique token with an index (an integer). The vocabularies of the source and target languages are distinct.

Using the min_freq argument, it only allow tokens that appear at least 2 times to appear in vocabulary. Tokens that appear only once are converted into an (unknown) token.

SRC.build_vocab(train_data, min_freq = 2)
TRG.build_vocab(train_data, min_freq = 2)

print(f"Unique tokens in source (de) vocabulary: {len(SRC.vocab)}")
print(f"Unique tokens in target (en) vocabulary: {len(TRG.vocab)}")
# Unique tokens in source (de) vocabulary: 7855
# Unique tokens in target (en) vocabulary: 5893
print(vars(SRC.vocab).keys()) # dict_keys(['freqs', 'itos', 'stoi', 'vectors'])
# freqs - frequency of each word
# itos - Every single word
# stoi - word2index

The final step of preparing the data is to create the iterators. These can be iterated on to return a batch of data which will have a src attribute (the PyTorch tensors containing a batch of numericalized source sentences) and a trg attribute (the PyTorch tensors containing a batch of numericalized target sentences). Numericalized is just a fancy way of saying they have been converted from a sequence of readable tokens to a sequence of corresponding indexes, using the vocabulary.

We also need to define a torch.device. This is used to tell TorchText to put the tensors on the GPU or not. We use the torch.cuda.is_available() function, which will return True if a GPU is detected on our computer. We pass this device to the iterator.

When we get a batch of examples using an iterator we need to make sure that all of the source sentences are padded to the same length, the same with the target sentences. Luckily, TorchText iterators handle this for us!

We use a BucketIterator instead of the standard Iterator as it creates batches in such a way that it minimizes the amount of padding in both the source and target sentences.

device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
print('cuda' if torch.cuda.is_available() else 'cpu')
print(torch.cuda.device_count() if torch.cuda.device_count() else 0)

BATCH_SIZE = 128

train_iterator, valid_iterator, test_iterator = BucketIterator.splits(
    (train_data, valid_data, test_data), 
    batch_size = BATCH_SIZE, 
    device = device)

print(vars(valid_iterator))
'''
{'_iterations_this_epoch': 0,
 '_random_state_this_epoch': None,
 '_restored_from_state': False,
 'batch_size': 128,
 'batch_size_fn': None,
 'dataset': <torchtext.datasets.translation.Multi30k at 0x7f9ff1852d68>,
 'device': device(type='cuda'),
 'iterations': 0,
 'random_shuffler': <torchtext.data.utils.RandomShuffler at 0x7f9f8e3c1588>,
 'repeat': False,
 'shuffle': False,
 'sort': True,
 'sort_key': <function torchtext.datasets.translation.TranslationDataset.sort_key>,
 'sort_within_batch': True,
 'train': False}
'''  
print(vars(vars(valid_iterator)['dataset']).keys(), len(vars(vars(valid_iterator)['dataset'])['examples'])) 
# dict_keys(['examples', 'fields']), all validation data --  len = 1014

Building the Seq2Seq Model

Encoder

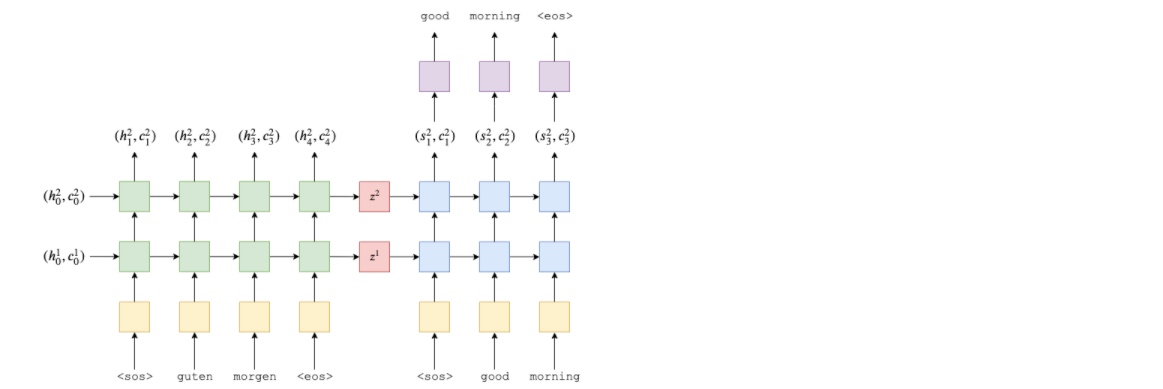
First, the encoder, a 2 layer LSTM (The paper uses a 4-layer LSTM).

For a multi-layer RNN, the input sentence, 𝑋 , after being embedded goes into the first (bottom) layer of the RNN and hidden states, $𝐻={ℎ_1,ℎ_2,...,ℎ_𝑇}$ , output by this layer are used as inputs to the RNN in the layer above. Thus, representing each layer with a superscript, the hidden states in the first layer are given by: $$ℎ^1_𝑡=EncoderRNN1(𝑒(𝑥_𝑡),ℎ^1_{𝑡−1}) $$ The hidden states in the second layer are given by: $$ℎ^2_𝑡=EncoderRNN1(ℎ^1_𝑡),ℎ^2_{𝑡−1}) $$ Using a multi-layer RNN, need an initial hidden state as input per layer, $ℎ^𝑙_0$ , and output a context vector per layer, $𝑧^𝑙$ .

LSTM is a type of RNN which instead of just taking in a hidden state and returning a new hidden state per time-step, also take in and return a cell state, $𝑐_𝑡$ , per time-step. $$ℎ_𝑡=RNN(𝑒(𝑥_𝑡),ℎ_{𝑡−1})$$ $$(ℎ_𝑡,𝑐_𝑡)=LSTM(𝑒(𝑥_𝑡),ℎ_{𝑡−1},𝑐_{𝑡−1}) $$ $𝑐_𝑡$ can be regarded as another type of hidden state. Similar to $ℎ^𝑙_0 , 𝑐^𝑙_0$ will be initialized to a tensor of all zeros. Also, context vector will now be both the final hidden state and the final cell state, i.e. $𝑧^𝑙=(ℎ^𝑙_𝑇,𝑐^𝑙_𝑇) $.

Extending multi-layer equations to LSTMs, can get $$(ℎ^1_𝑡,𝑐^1_𝑡)=EncoderLSTM^1(𝑒(𝑥_𝑡),(ℎ^1_{𝑡−1},𝑐^1_{𝑡−1}))$$ $$(ℎ^2_𝑡,𝑐^2_𝑡)=EncoderLSTM^2(ℎ^1_𝑡,(ℎ^2_{𝑡−1},𝑐^2_{𝑡−1}))$$ Note how only hidden state from the first layer is passed as input to the second layer, and not the cell state.

So the encoder looks something like this:

Can create this in code by making an Encoder module, which requires we inherit from torch.nn.Module and use the super().__init__() as some boilerplate code. The encoder takes the following arguments:

• input_dim is the size/dimensionality of the one-hot vectors that will be input to the encoder. This is equal to the input (source) vocabulary size.
• emb_dim is the dimensionality of the embedding layer. This layer converts the one-hot vectors into dense vectors with emb_dim dimensions.
• hid_dim is the dimensionality of the hidden and cell states.
• n_layers is the number of layers in the RNN.
• dropout is the amount of dropout to use. This is a regularization parameter to prevent overfitting. Check out this for more details about dropout.

The embedding layer(a step before the indexes of the words) is created using nn.Embedding, the LSTM with nn.LSTM and a dropout layer with nn.Dropout. (Good articles for word embedding,1,2,3,4)

One thing to note is that the dropout argument to the LSTM is how much dropout to apply between the layers of a multi-layer RNN, i.e. between the hidden states output from layer $𝑙$ and those same hidden states being used for the input of layer $𝑙+1$ .

In the forward function, pass in the source sentence, 𝑋 , which is converted into dense vectors using the embedding layer, and then dropout is applied. These embeddings are then passed into the RNN. As pass a whole sequence to the RNN, it will automatically do the recurrent calculation of the hidden states over the whole sequence for us! Notice that if no hidden/cell state is passed to the RNN, it will automatically create an initial hidden/cell state as a tensor of all zeros.

The RNN returns:

• outputs (the top-layer hidden state for each time-step)
• hidden (the final hidden state for each layer, $ℎ_𝑇$ , stacked on top of each other)
• cell (the final cell state for each layer, $𝑐_𝑇$ , stacked on top of each other)

As Decoder only need the final hidden and cell states (to make context vector), forward function only returns hidden and cell.

In this implementation n_directions will always be 1, however note that bidirectional RNNs will have n_directions as 2.

class Encoder(nn.Module):
    def __init__(self, input_dim, emb_dim, hid_dim, n_layers, dropout):
        super().__init__()
        
        self.hid_dim = hid_dim
        self.n_layers = n_layers
        
        self.embedding = nn.Embedding(input_dim, emb_dim)
        
        self.rnn = nn.LSTM(emb_dim, hid_dim, n_layers, dropout = dropout)
        
        self.dropout = nn.Dropout(dropout)
        
    def forward(self, src):
        
        #src = [src len, batch size]
        
        embedded = self.dropout(self.embedding(src))
        
        #embedded = [src len, batch size, emb dim]
        
        outputs, (hidden, cell) = self.rnn(embedded)
        
        #outputs  = [src len, batch size, hid dim * n directions]
        #hidden = [n layers * n directions, batch size, hid dim]
        #cell = [n layers * n directions, batch size, hid dim]
        
        #outputs are always from the top hidden layer
        
        return hidden, cell

Decoder

Build decoder, which will also be a 2-layer (4 in the paper) LSTM.

The Decoder class does a single step of decoding, i.e. it outputs single token per time-step. The first layer will receive a hidden and cell state from the previous time-step, $(𝑠^1_{𝑡−1},𝑐^1_{𝑡−1})$ , and feeds it through the LSTM with the current embedded token, $𝑦_𝑡$ (Remember that the first embedded token should be the embedded ‘’), to produce a new hidden and cell state, $(𝑠^1_t,𝑐^1_t)$ . The subsequent layers will use the hidden state from the layer below, $𝑠^{𝑙−1}_𝑡$ , and the previous hidden and cell states from their layer, $(𝑠^1_{𝑡−1},𝑐^1_{𝑡−1})$ . This provides equations very similar to those in the encoder. $$(𝑠^1_𝑡,𝑐^1_𝑡)=DecoderLSTM^1(𝑑(𝑦_𝑡),(𝑠^1_{𝑡−1},𝑐^1_{𝑡−1}))$$ $$(𝑠^2_𝑡,𝑐^2_𝑡)=DecoderLSTM^2(𝑠^1_𝑡,(𝑠^2_{𝑡−1},𝑐^2_{𝑡−1}))$$ Remember that the initial hidden and cell states to our decoder are our context vectors, which are the final hidden and cell states of our encoder from the same layer, i.e. $(𝑠^𝑙_0,𝑐^𝑙_0)=𝑧^𝑙=(ℎ^𝑙_𝑇,𝑐^𝑙_𝑇)$ .

Then pass the hidden state from the top layer of the RNN, $𝑠^𝐿_𝑡$ , through a linear layer, 𝑓 , to make a prediction of what the next token in the target (output) sequence should be, $𝑦̂_{𝑡+1}$ . $$𝑦̂_{𝑡+1}=𝑓(𝑠^𝐿_𝑡) $$ The arguments and initialization are similar to the Encoder class, except now have an output_dim which is the size of the vocabulary for the output/target. There is also the addition of the Linear layer used to make the predictions from the top layer hidden state.

Within the forward function, it accept a batch of input tokens, previous hidden states and previous cell states. As it is only decoding one token at a time, the input tokens will always have a sequence length of 1. Unsqueeze the input tokens to add a sentence length dimension of 1. Then, similar to the encoder, pass through an embedding layer and apply dropout. This batch of embedded tokens is then passed into the RNN with the previous hidden and cell states. This produces an output (hidden state from the top layer of the RNN), a new hidden state (one for each layer, stacked on top of each other) and a new cell state (also one per layer, stacked on top of each other). Then pass the output (after getting rid of the sentence length dimension) through the linear layer to receive prediction. Then return the prediction, the new hidden state and the new cell state.

Note(optional): as we always have a sequence length of 1, we could use nn.LSTMCell(just a single cell), instead of nn.LSTM(a wrapper around potentially multiple cells), as it is designed to handle a batch of inputs that aren’t necessarily in a sequence. Using the nn.LSTMCell in this case would mean we don’t have to unsqueeze to add a fake sequence length dimension, but we would need one nn.LSTMCell per layer in the decoder and to ensure each nn.LSTMCell receives the correct initial hidden state from the encoder.

class Decoder(nn.Module):
    def __init__(self, output_dim, emb_dim, hid_dim, n_layers, dropout):
        super().__init__()
        
        self.output_dim = output_dim
        self.hid_dim = hid_dim
        self.n_layers = n_layers
        
        self.embedding = nn.Embedding(output_dim, emb_dim)
        
        self.rnn = nn.LSTM(emb_dim, hid_dim, n_layers, dropout = dropout)
        
        self.fc_out = nn.Linear(hid_dim, output_dim)
        
        self.dropout = nn.Dropout(dropout)
        
    def forward(self, input, hidden, cell):
        
        #input = [batch size]
        #hidden = [n layers * n directions, batch size, hid dim]
        #cell = [n layers * n directions, batch size, hid dim]
        
        #n directions in the decoder will both always be 1, therefore:
        #hidden = [n layers, batch size, hid dim]
        #context = [n layers, batch size, hid dim]
        
        input = input.unsqueeze(0)
        
        #input = [1, batch size]
        
        embedded = self.dropout(self.embedding(input))
        
        #embedded = [1, batch size, emb dim]
                
        output, (hidden, cell) = self.rnn(embedded, (hidden, cell))
        
        #output = [seq len, batch size, hid dim * n directions]
        #hidden = [n layers * n directions, batch size, hid dim]
        #cell = [n layers * n directions, batch size, hid dim]
        
        #seq len and n directions will always be 1 in the decoder, therefore:
        #output = [1, batch size, hid dim]
        #hidden = [n layers, batch size, hid dim]
        #cell = [n layers, batch size, hid dim]
        
        prediction = self.fc_out(output.squeeze(0))
        
        #prediction = [batch size, output dim]
        
        return prediction, hidden, cell

Seq2seq

For the final part of the implemenetation - seq2seq model. This will handle:

• receiving the input/source sentence
• using the encoder to produce the context vectors
• using the decoder to produce the predicted output/target sentence

Full model will look like this:

The Seq2Seq model takes in an Encoder, Decoder, and a device (used to place tensors on the GPU, if it exists).

(Optional)For this implementation, need to ensure that the number of layers and the hidden (and cell) dimensions are equal in the Encoder and Decoder. This is not always the case, it is not necessarily need the same number of layers or the same hidden dimension sizes in a sequence-to-sequence model. However, if did something like having a different number of layers then it would need to make decisions about how this is handled. For example, if our encoder has 2 layers and our decoder only has 1, how is this handled? Do we average the two context vectors output by the decoder? Do we pass both through a linear layer? Do we only use the context vector from the highest layer? Etc.

Forward function takes the source sentence, target sentence and a teacher-forcing ratio(used when training model). When decoding, at each time-step it will predict what the next token in the target sequence will be from the previous tokens decoded, $ 𝑦̂_{𝑡+1}=𝑓(𝑠^𝐿_𝑡)$ . With probability equal to the teaching forcing ratio, it will use the actual ground-truth next token in the sequence as the input to the decoder during the next time-step. However, with probability (1 - teacher_forcing_ratio), it will use the token that the model predicted as the next input to the model, even if it doesn’t match the actual next token in the sequence.

The first thing in the forward function is to create an outputs tensor that will store all of our predictions, $𝑌̂$ .

Then feed the input/source sentence, src, into the encoder and receive out final hidden and cell states.

The first input to the decoder is the start of sequence () token. As our trg tensor already has the token appended (all the way back when we defined the init_token in our TRG field) we get our 𝑦1 by slicing into it. We know how long our target sentences should be (max_len), so we loop that many times. The last token input into the decoder is the one before the token - the token is never input into the decoder.

During each iteration of the loop, we:

• pass the input, previous hidden and previous cell states ($y_t, s_{t-1}, c_{t-1}$) into the decoder
• receive a prediction, next hidden state and next cell state ($\hat{y}_{t+1}, s_{t}, c_{t}$) from the decoder
• place prediction, $\hat{y}_{t+1}$/output in tensor of predictions, $\hat{Y}$/outputs
• decide if use “teacher force” or not
  • if so, the next input is the ground-truth next token in the sequence, $y_{t+1}$/trg[t]
  • if not, the next input is the predicted next token in the sequence, $\hat{y}_{t+1}$/top1, which we get by doing an argmax over the output tensor

Once made all of predictions, return tensor full of predictions, $\hat{Y}$/outputs.

Note: decoder loop starts at 1, not 0. This means the 0th element of our outputs tensor remains all zeros. So trg and outputs look something like: $$trg=[<𝑠𝑜𝑠>,𝑦_1,𝑦_2,𝑦_3,<𝑒𝑜𝑠>] $$ $$outputs=[0,𝑦̂_1,𝑦̂_2,𝑦̂_3,<𝑒𝑜𝑠>]$$ Later on when calculate the loss, can cut off the first element of each tensor to get: $$trg=[𝑦_1,𝑦_2,𝑦_3,<𝑒𝑜𝑠>] $$ $$outputs=[𝑦̂_1,𝑦̂_2,𝑦̂_3,<𝑒𝑜𝑠>]$$

class Seq2Seq(nn.Module):
    def __init__(self, encoder, decoder, device):
        super().__init__()
        
        self.encoder = encoder
        self.decoder = decoder
        self.device = device
        
        assert encoder.hid_dim == decoder.hid_dim, \
            "Hidden dimensions of encoder and decoder must be equal!"
        assert encoder.n_layers == decoder.n_layers, \
            "Encoder and decoder must have equal number of layers!"
        
    def forward(self, src, trg, teacher_forcing_ratio = 0.5):
        
        #src = [src len, batch size]
        #trg = [trg len, batch size]
        #teacher_forcing_ratio is probability to use teacher forcing
        #e.g. if teacher_forcing_ratio is 0.75 we use ground-truth inputs 75% of the time
        
        batch_size = trg.shape[1]
        trg_len = trg.shape[0]
        trg_vocab_size = self.decoder.output_dim
        
        #tensor to store decoder outputs
        outputs = torch.zeros(trg_len, batch_size, trg_vocab_size).to(self.device)
        # 128(batch_size)个例子, 每个例子里的句子长度为32(trg_len), 每个句子里的单词都有5893维(vacab_size)

        #last hidden state of the encoder is used as the initial hidden state of the decoder
        hidden, cell = self.encoder(src)
        
        #first input to the decoder is the <sos> tokens
        input = trg[0,:]
        
        for t in range(1, trg_len):
            
            #insert input token embedding, previous hidden and previous cell states
            #receive output tensor (predictions) and new hidden and cell states
            output, hidden, cell = self.decoder(input, hidden, cell)
            
            #place predictions in a tensor holding predictions for each token
            outputs[t] = output
            
            #decide if we are going to use teacher forcing or not
            teacher_force = random.random() < teacher_forcing_ratio
            
            #get the highest predicted token from our predictions
            top1 = output.argmax(1) 
            
            #if teacher forcing, use actual next token as next input
            #if not, use predicted token
            input = trg[t] if teacher_force else top1
        
        return outputs

Training the Seq2Seq Model

Firstly, initialize model. As mentioned before, the input and output dimensions are defined by the size of the vocabulary. The embedding dimesions and dropout for the encoder and decoder can be different, but the number of layers and the size of the hidden/cell states must be the same.

Then define the encoder, decoder and then Seq2Seq model, which place on the device.

INPUT_DIM = len(SRC.vocab) # 7855
OUTPUT_DIM = len(TRG.vocab) # 5893
ENC_EMB_DIM = 256
DEC_EMB_DIM = 256
HID_DIM = 512
N_LAYERS = 2
ENC_DROPOUT = 0.5
DEC_DROPOUT = 0.5

enc = Encoder(INPUT_DIM, ENC_EMB_DIM, HID_DIM, N_LAYERS, ENC_DROPOUT)
dec = Decoder(OUTPUT_DIM, DEC_EMB_DIM, HID_DIM, N_LAYERS, DEC_DROPOUT)

model = Seq2Seq(enc, dec, device).to(device)

Next up is initializing the weights of model. In the paper they state they initialize all weights from a uniform distribution between -0.08 and +0.08, i.e. $\mathcal{U}(-0.08, 0.08)$.

Initialize weights in PyTorch by creating a function which apply to model. When using apply, the init_weights function will be called on every module and sub-module within model. For each module will loop through all of the parameters and sample them from a uniform distribution with nn.init.uniform_.

def init_weights(m):
    for name, param in m.named_parameters():
        nn.init.uniform_(param.data, -0.08, 0.08)
        
model.apply(init_weights)
'''
Seq2Seq(
  (encoder): Encoder(
    (embedding): Embedding(7855, 256)
    (rnn): LSTM(256, 512, num_layers=2, dropout=0.5)
    (dropout): Dropout(p=0.5, inplace=False)
  )
  (decoder): Decoder(
    (embedding): Embedding(5893, 256)
    (rnn): LSTM(256, 512, num_layers=2, dropout=0.5)
    (fc_out): Linear(in_features=512, out_features=5893, bias=True)
    (dropout): Dropout(p=0.5, inplace=False)
  )
)
'''

Define a function that will calculate the number of trainable parameters in the model.

def count_parameters(model):
    return sum(p.numel() for p in model.parameters() if p.requires_grad)

print(f'The model has {count_parameters(model):,} trainable parameters') # The model has 13,899,013 trainable parameters

Define optimizer - Adam, which will use to update our parameters in the training loop. Check out this post for information about different optimizers.

Next, define loss function. The CrossEntropyLoss function calculates both the log softmax as well as the negative log-likelihood of predictions.

Loss function calculates the average loss per token, however by passing the index of the token as the ignore_index argument, it will ignore the loss whenever the target token is a padding token.

optimizer = optim.Adam(model.parameters())

TRG_PAD_IDX = TRG.vocab.stoi[TRG.pad_token]
print(TRG.pad_token)  # <pad>
print(TRG.vocab.stoi[TRG.pad_token]) # 1 

criterion = nn.CrossEntropyLoss(ignore_index = TRG_PAD_IDX)

Next, define training loop. First, set the model into “training mode” with model.train(). This will turn on dropout (and batch normalization, which aren’t using here) and then iterate through data iterator.

As stated before, decoder loop starts at 1, not 0. This means the 0th element of outputs tensor remains all zeros. So trg and outputs look something like: $$trg=[<𝑠𝑜𝑠>,𝑦_1,𝑦_2,𝑦_3,<𝑒𝑜𝑠>] $$ $$outputs=[0,𝑦̂_1,𝑦̂_2,𝑦̂_3,<𝑒𝑜𝑠>]$$ Here, when calculate the loss, cut off the first element of each tensor to get: $$trg=[𝑦_1,𝑦_2,𝑦_3,<𝑒𝑜𝑠>] $$ $$outputs=[𝑦̂_1,𝑦̂_2,𝑦̂_3,<𝑒𝑜𝑠>]$$

At each iteration:

• get the source and target sentences from the batch, $X$ and $Y$
• zero the gradients calculated from the last batch
• feed the source and target into the model to get the output, $\hat{Y}$
• as the loss function only works on 2d inputs with 1d targets, need to flatten each of them with .view
• slice off the first column of the output and target tensors ( part) as mentioned above
• calculate the gradients with loss.backward()
• clip the gradients to prevent them from exploding (a common issue in RNNs)
• update the parameters of our model by doing an optimizer step
• sum the loss value to a running total

Finally, return the loss that is averaged over all batches.

epoch_loss = 0
for i, batch in enumerate(train_iterator):
  # print(i,batch)
  src = batch.src
  trg = batch.trg
    
  output = model(src, trg)
  output_dim = output.shape[-1]  # 5893

  new_output = output[1:].view(-1, output_dim)  # remove <sos>, [out len * batchsize, output dim]
  new_trg = trg[1:].view(-1)  # remove <sos> , [trg len * batchsize]
    
  loss = criterion(new_output, new_trg)
  epoch_loss += loss.item()
print(epoch_loss / len(train_iterator)) # 3.0412618011104904
'''
src size: [27, 128], trg size: [24, 128], output size: [24, 128, 5893], output[1:]:[23, 128, 5893], new_output: [2944, 5893], new trg size: [2944], loss: 2.9742650985717773
src size: [28, 128], trg size: [27, 128], output size: [27, 128, 5893], output[1:]:[26, 128, 5893], new_output: [3328, 5893], new trg size: [3328], loss: 3.1595866680145264
src size: [32, 128], trg size: [28, 128], output size: [28, 128, 5893], output[1:]:[27, 128, 5893], new_output: [3456, 5893], new trg size: [3456], loss: 2.8984110355377197
src size: [30, 128], trg size: [31, 128], output size: [31, 128, 5893], output[1:]:[30, 128, 5893], new_output: [3840, 5893], new trg size: [3840], loss: 3.348358392715454
src size: [24, 128], trg size: [27, 128], output size: [27, 128, 5893], output[1:]:[26, 128, 5893], new_output: [3328, 5893], new trg size: [3328], loss: 2.9191009998321533
....
'''

def train(model, iterator, optimizer, criterion, clip):
    
    model.train()
    
    epoch_loss = 0
    
    for i, batch in enumerate(iterator):
        
        src = batch.src
        trg = batch.trg
        
        optimizer.zero_grad()
        
        output = model(src, trg)
        
        #trg = [trg len, batch size]
        #output = [trg len, batch size, output dim]
        
        output_dim = output.shape[-1]
        
        output = output[1:].view(-1, output_dim)
        trg = trg[1:].view(-1)
        
        #trg = [(trg len - 1) * batch size]
        #output = [(trg len - 1) * batch size, output dim]
        
        loss = criterion(output, trg)
        
        loss.backward()
        
        torch.nn.utils.clip_grad_norm_(model.parameters(), clip)
        
        optimizer.step()
        
        epoch_loss += loss.item()
        
    return epoch_loss / len(iterator)

Evaluation loop is similar to training loop, however as there is not need to update any parameters, so don’t need to pass an optimizer or a clip value.

Remember to set the model to evaluation mode with model.eval(). This will turn off dropout (and batch normalization, if used).

Use the with torch.no_grad() block to ensure no gradients are calculated within the block. This reduces memory consumption and speeds things up.

The iteration loop is similar (without the parameter updates), however need to ensure turn teacher forcing off for evaluation. This will cause the model to only use it’s own predictions to make further predictions within a sentence, which mirrors how it would be used in deployment.

def evaluate(model, iterator, criterion):
    
    model.eval()
    
    epoch_loss = 0
    
    with torch.no_grad():
    
        for i, batch in enumerate(iterator):

            src = batch.src
            trg = batch.trg

            output = model(src, trg, 0) #turn off teacher forcing

            #trg = [trg len, batch size]
            #output = [trg len, batch size, output dim]

            output_dim = output.shape[-1]
            
            output = output[1:].view(-1, output_dim)
            trg = trg[1:].view(-1)

            #trg = [(trg len - 1) * batch size]
            #output = [(trg len - 1) * batch size, output dim]

            loss = criterion(output, trg)
            
            epoch_loss += loss.item()
        
    return epoch_loss / len(iterator)

Next, create a function that will use to tell how long an epoch takes.

def epoch_time(start_time, end_time):
    elapsed_time = end_time - start_time
    elapsed_mins = int(elapsed_time / 60)
    elapsed_secs = int(elapsed_time - (elapsed_mins * 60))
    return elapsed_mins, elapsed_secs

Start training our model. At each epoch, check if model has achieved the best validation loss so far. If it has, update best validation loss and save the parameters of model (called state_dict in PyTorch). Then, when it come to test model, use the saved parameters used to achieve the best validation loss.

Print out both the loss and the perplexity(math.exp) at each epoch. It is easier to see a change in perplexity than a change in loss as the numbers are much bigger.

N_EPOCHS = 10
CLIP = 1

best_valid_loss = float('inf')

for epoch in range(N_EPOCHS):
    
    start_time = time.time()
    
    train_loss = train(model, train_iterator, optimizer, criterion, CLIP)
    valid_loss = evaluate(model, valid_iterator, criterion)
    
    end_time = time.time()
    
    epoch_mins, epoch_secs = epoch_time(start_time, end_time)
    
    if valid_loss < best_valid_loss:
        best_valid_loss = valid_loss
        torch.save(model.state_dict(), 'tut1-model.pt')
    
    print(f'Epoch: {epoch+1:02} | Time: {epoch_mins}m {epoch_secs}s')
    print(f'\tTrain Loss: {train_loss:.3f} | Train PPL: {math.exp(train_loss):7.3f}')
    print(f'\t Val. Loss: {valid_loss:.3f} |  Val. PPL: {math.exp(valid_loss):7.3f}')
'''
Epoch: 01 | Time: 0m 26s
	Train Loss: 5.058 | Train PPL: 157.313
	 Val. Loss: 4.922 |  Val. PPL: 137.291
Epoch: 02 | Time: 0m 24s
	Train Loss: 4.480 | Train PPL:  88.252
	 Val. Loss: 4.815 |  Val. PPL: 123.300
Epoch: 03 | Time: 0m 23s
	Train Loss: 4.179 | Train PPL:  65.320
	 Val. Loss: 4.617 |  Val. PPL: 101.208
Epoch: 04 | Time: 0m 24s
	Train Loss: 3.964 | Train PPL:  52.676
	 Val. Loss: 4.547 |  Val. PPL:  94.344
Epoch: 05 | Time: 0m 23s
	Train Loss: 3.799 | Train PPL:  44.677
	 Val. Loss: 4.486 |  Val. PPL:  88.726
Epoch: 06 | Time: 0m 24s
	Train Loss: 3.658 | Train PPL:  38.791
	 Val. Loss: 4.307 |  Val. PPL:  74.192
Epoch: 07 | Time: 0m 24s
	Train Loss: 3.515 | Train PPL:  33.625
	 Val. Loss: 4.136 |  Val. PPL:  62.564
Epoch: 08 | Time: 0m 23s
	Train Loss: 3.366 | Train PPL:  28.976
	 Val. Loss: 4.016 |  Val. PPL:  55.463
Epoch: 09 | Time: 0m 24s
	Train Loss: 3.224 | Train PPL:  25.135
	 Val. Loss: 3.949 |  Val. PPL:  51.870
Epoch: 10 | Time: 0m 25s
	Train Loss: 3.125 | Train PPL:  22.770
	 Val. Loss: 3.913 |  Val. PPL:  50.025
'''

Load the parameters (state_dict) that gave model the best validation loss and run it the model on the test set.

model.load_state_dict(torch.load('tut1-model.pt'))

test_loss = evaluate(model, test_iterator, criterion)

print(f'| Test Loss: {test_loss:.3f} | Test PPL: {math.exp(test_loss):7.3f} |')
#  Test Loss: 3.896 | Test PPL:  49.208 |

Save model to gdrive

from google.colab import drive
drive.mount('/content/gdrive')

model_save_name = 'tut1-model.pt'
path = F"/content/gdrive/My Drive/{model_save_name}" 
torch.save(model.state_dict(), path)

Translate sentence

def translate_sentence(sentence,src_field,trg_field,model,device, max_len=50):
    model.eval()

    if isinstance(sentence,str):
        nlp = spacy.load('de')
        tokens = [token.text.lower() for token in nlp(sentence)]
    else:
        tokens = [token.lower() for token in sentence]

    tokens = [src_field.init_token] + tokens + [src_field.eos_token]

    src_indexes = [src_field.vocab.stoi[token] for token in tokens]
    src_tensor = torch.LongTensor(src_indexes).unsqueeze(1).to(device)

    with torch.no_grad():
        hidden, cell = model.encoder(src_tensor)

    trg_indexes = [trg_field.vocab.stoi[trg_field.init_token]]

    #
    for i in range(max_len):
        trg_tensor = torch.LongTensor([trg_indexes[-1]]).to(device)

        with torch.no_grad():
            output, hidden, cell = model.decoder(trg_tensor, hidden, cell)
        pred_token = output.argmax(1).item()
        trg_indexes.append(pred_token)
        if pred_token == trg_field.vocab.stoi[trg_field.eos_token]:
            break
    trg_tokens = [trg_field.vocab.itos[i] for i in trg_indexes]

    return trg_tokens[1:-1] # remove <sos> and <eos>

example_idx = 12

src = vars(train_data.examples[example_idx])['src']
trg = vars(train_data.examples[example_idx])['trg']

print(f'src = {src}')
print(f'trg = {trg}')

translation = translate_sentence(src, SRC, TRG, model, device)

print(f'predicted trg = {translation}')