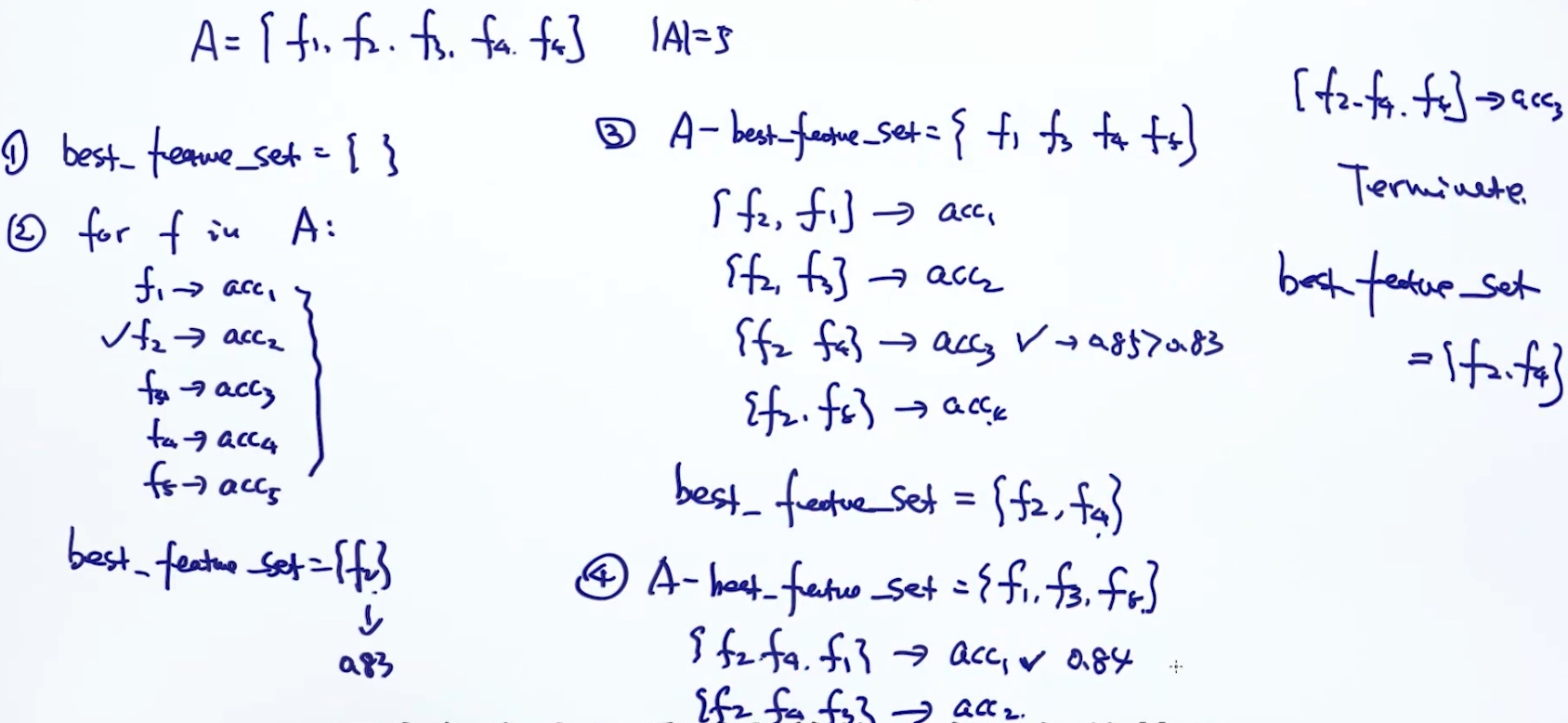NLP2
AI系统
符号主义 - 专家系统(Expert System), rule-based
- If conditions:
- Then do…
- 适用于没有/很少数据的情况
- E.g. 意图识别
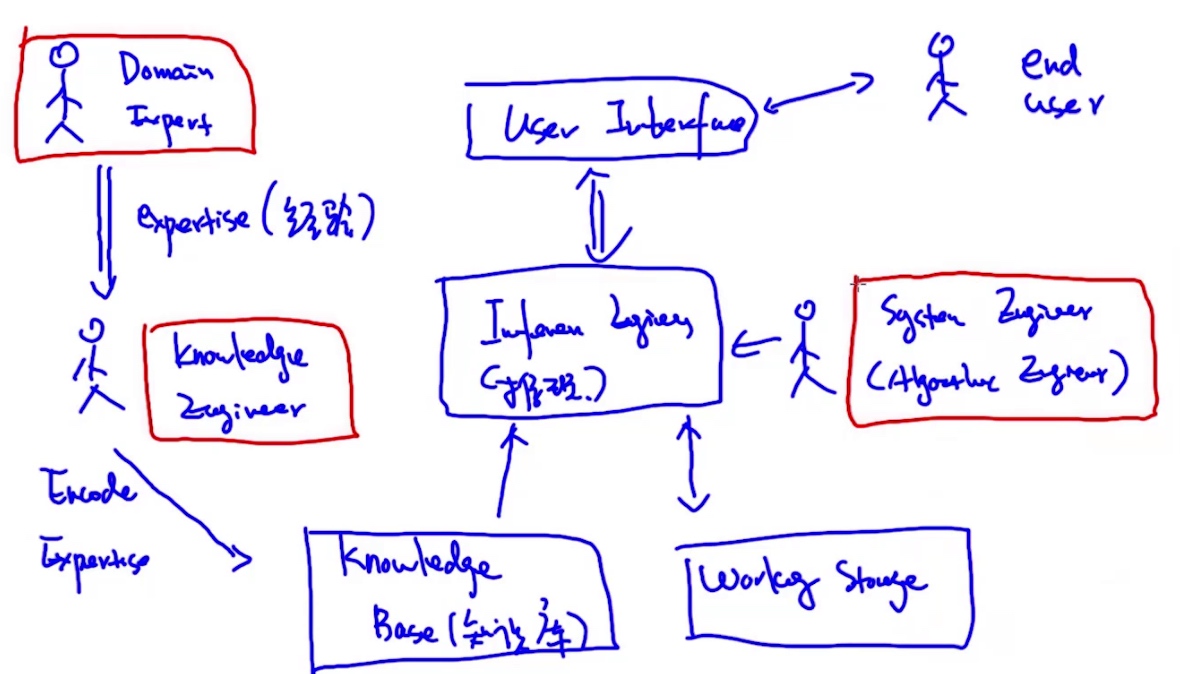
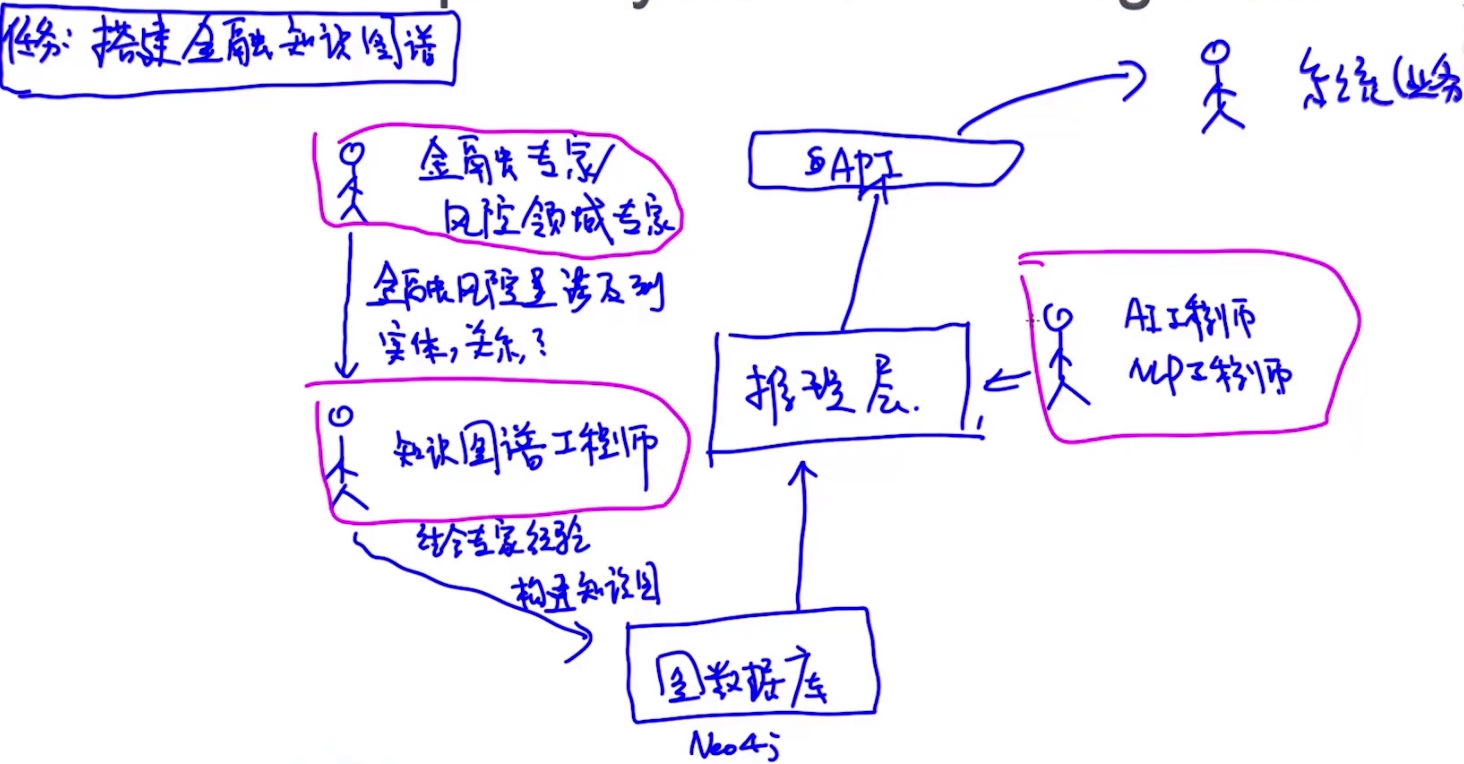
- 专家系统 = 推理引擎 + 知识
- Expert System’s Working Flow
- Properties:
- 处理不确定性
- 知识的表示 (知识图谱)
- 可解释性 (与DL end-to-end模型完全相反)
- 可以做知识推理
- Drawbacks:
- 设计大量的规则 (Design lots of Rules)
- 需要领域专家来主导 (Heavily rely on Domain expert)
- 可移植性差 (Limited transferability to other domain)
- 学习能力差 (Inability to learn)
- 人能考虑的范围是有限的 (Human capacity is limited)
- Problems:
- 逻辑推理 (Logical Inference)
- Forward Chaining Algorithm
- Backward Chaining Algorithm
- 解决规则冲突 (Conflict Resolution)
- 通过逻辑推理来判断冲突与否
- 选择最小规则的子集 (Minimum size of rules)
- 贪心算法…
- 逻辑推理 (Logical Inference)
连接主义 - 基于概率的系统(Probabilistic)
- 给定数据 D = {X,y}
- 学习X到y的映射关系
- f: X -> y
- 适用大量数据的情况
AI系统 VS BI系统:
- BI系统将数据整合封装, 用户从这些数据找到规律, 辅助做出决策
- AI系统帮助/替代用户去做决策
机器学习
定义:
自动从已有的数据里找出一些规律, 然后把学到的这些规律应用到对未来数据的预测中, 或者在不确定环境下自动地做一些决策
分类:
| Supervised Learning | Unsupervised Learning | |
|---|---|---|
| Generative Model | Naive Bayes | HMM LDA GMM |
| Discriminative Model | Logistic Regress Conditional Random Field (CRF) | N/A |
生成模型 VS 判别模型
生成模型:
- 用联合概率训练, 目标函数是最大化 P(X) or P(Xy)
- 可以生成新的数据, 图片,音乐,文本,…
- 建立分类器, 会记住所有特征细节
判别模型:
- 用条件概率训练, 目标函数是最大化 P(y|X)
- 建立分类器, 会记住所有区别
Classic Working Pipeline
- 数据 –> Cleaning –> 特征工程(针对问题从数据中提取特征) –> 建模 -> 预测
- 特征工程时间成本高
- 特征确定了系统性能的上限
End-to-End Learning
- 数据 –> Cleaning –> 建模 -> 预测
Naive Bayes
Bayes Therom
$P(x|y) = \frac{P(y|x)P(x)}{P(y)}$
Conditional Independence
$P(x,y|z) = P(x|z)P(y|z)$- x,y是条件独立于z
垃圾邮件判断例子
- 新邮件: ‘购买物品, 不是广告’
$P(正常|内容) >? P(垃圾|内容)$$\frac{P(内容|正常)P(正常)}{P(内容)} >? \frac{P(内容|垃圾)P(垃圾)}{P(内容)}$$P(内容|正常)P(正常) >? P(内容|垃圾)P(垃圾)$- P(正常) 和 P(垃圾) 是先验概率 (已知的)
$P(内容|正常) = P('购买,物品,不是,广告'|正常)$$P(内容|正常) = P('购买'|正常)P('物品'|正常)P('不是'|正常)P('广告'|正常)$
 - 计算条件概率的时候使用了laplace smoothing
- 在所有概率相乘的时候可以加个log函数防止underflow的情况出现
- 概率连乘得出的结果太小
- log函数严格单调递增
- 加上log函数不影响对比
- 计算条件概率的时候使用了laplace smoothing
- 在所有概率相乘的时候可以加个log函数防止underflow的情况出现
- 概率连乘得出的结果太小
- log函数严格单调递增
- 加上log函数不影响对比
求最优解 (closed-form)
- 闭式解(closed form solution)也叫解析解(analytical solution),就是一些严格的公式,给出任意的自变量就可以求出其因变量,也就是问题的解, 他人可以利用这些公式计算各自的问题
- 所谓的解析解是一种包含分式、三角函数、指数、对数甚至无限级数等基本函数的解的形式. 用来求得解析解的方法称为解析法(analytic techniques),解析法即是常见的微积分技巧,例如分离变量法等
- 解析解为一封闭形式(closed-form)的函数,因此对任一独立变量,皆可将其带入解析函数求得正确的相应变量
求极值
$f(x) = x^2 - 2x - 3$:
$x = -\frac{b}{2a} = 1$$f'(x) = 2x-2 = 0$==> x = 1- gradient descent (1st order)
$x^t = x^{t-1} - \alpha \delta f(x)$
- Newton’s method (2nd order)
有限制条件的优化 (constrain optimization)
$$
f(x,y) = x + y
s.t. x^2 + y^2 = 1
$$
拉格朗日乘法项 (lagrangian Multiplier)
当条件为等式的时候:
- 把条件放入目标函数 (相当于把条件作为目标函数的惩罚项)(把条件去掉了)
- maximize
$L(x,y,\lambda) = x+y + \lambda (x^2+y^2-1)$ - 求L的偏导 (偏导, 因为L的参数超过1个), 使其为0:
$\frac{\partial L(x,y,\lambda)}{\partial x} = 1+2\lambda x = 0$$\frac{\partial L(x,y,\lambda)}{\partial y} = 1+2\lambda y = 0$$\frac{\partial L(x,y,\lambda)}{\partial \lambda} = x^2+y^2-1 = 0$$x = -\frac{1}{2\lambda}, y = -\frac{1}{2\lambda}, (-\frac{1}{2\lambda})^2+(-\frac{1}{2\lambda})^2-1 = 0$$ \lambda_1 = \frac{\sqrt 2}{2},\lambda_2 = -\frac{\sqrt 2}{2} $$(x,y) => (\frac{\sqrt 2}{2},\frac{\sqrt 2}{2})$$(x,y) => (-\frac{\sqrt 2}{2},-\frac{\sqrt 2}{2})$
当条件为不等式的时候:
- …
MLE(Maximum Likelihood Estimation) 最大似然
构建目标函数:
- MLE (通过观测到的数据)
- 当样本数量太过少时不适用
- # of samples -> inf, MAP -> MLE
- MAP (采用专家/先验的经验)
- Bayesian (采用集成模型的思路)
D = {H,T,T,H,H,H} —MLE—> $\theta: 出现正面的概率 = \frac{2}{3}$
- step1: 构建目标函数
$max P(D) = P(H,T,T,H,H,H)$$ = P(H)P(T)P(T)P(H)P(H)P(H)$$ = \theta (1-\theta) (1-\theta)\theta\theta\theta $$ = \theta^4(1-\theta)^2$
- steps2: 优化
$L(\theta) = argmax_{\theta}\theta^4(1-\theta)^2$$\frac{\partial L(\theta)}{\partial \theta} = \theta^4 2(1-\theta)(-1)+ 4 \theta^3 (1-\theta)^2 = 0$$\theta = \frac{2}{3}$
模型 -> 模型实例化(# layers, loss function…) -> 优化
KL散度、交叉熵与极大似然 的关系
这3个东西其实是等价的.
一. 信息论背景
信息论的研究内容,是对一个信号包含信息的多少进行量化。所采用的量化指标最好满足两个条件:
- (1)越不可能发生的事件包含的信息量越大
- (2)独立事件有增量的信息(就是几个独立事件同时发生的信息量等于每一个信息量的和)
遵循以上原则,定义一个事件𝗑=𝑥的自信息为:
$𝐼(𝑥)=−log𝑝(𝑥)$- log底为e时,单位为nats;底为2时,单位为比特或香农
用香农熵(Shannon Entropy)对一个变量在整个概率分布中的不确定性进行量化:
$𝐻(𝗑)=𝐸_{𝗑∼𝑃}[𝐼(𝑥)]=𝐸_{𝗑∼𝑃}[-log𝑃(𝑥)] = -\sum_x P(x)logP(x)$- 香农熵的意义,就是满足𝑝分布的事件所产生的期望信息总量
- 如果log的base是2,熵可以认为是衡量编码对应的信息需要的最少bits数;那么交叉熵就是来衡量用特定的编码方案Q来对分布为P的信息x进行编码时需要的最少的bits数. 定义如下:
$H(P, Q)=-\Sigma_xP(x)log(Q(x))$
- 在深度学习中,P是ground tureth label的真实分布;Q就是网络学习后输出的分布
二. KL散度(Kullback-Leibler Divergence)
若一个随机变量𝗑有两种可能的分布𝑃(𝗑)和𝑄(𝗑),则可以用KL散度衡量两个分布之间的差异 (在深度学习中,KL散度用来评估模型输出的预测值分布与真值分布之间的差异):
$\begin{align*} D_{KL}(P||Q)&=E_{\mathsf{x}\sim P}\left[ \log \frac{P(x)}{Q(x)}\right]\\&=E_{\mathsf{x}\sim P} \left[ \log P(x)-\log Q(x)\right] \\&=\Sigma_{x=1}^NP(x)[logP(x)-logQ(x)] \end{align*} $- KL散度为非负,当且仅当P与Q为相同分布时,KL散度为零. 所以假设有一个分布𝑝(𝑥),想用另一个分布𝑞(𝑥)近似,可以选择最小化二者之间的KL散度
- 但是需注意
$𝐷_{𝐾𝐿}(𝑝||𝑞)≠𝐷_{𝐾𝐿}(𝑞||𝑝)$,前者表示选择一个q,使得它在p具有高概率的地方具有高概率;后者表示选择一个q,使得它在具有低概率的地方具有低概率
三. 交叉熵(Cross-Entropy)
交叉熵定义为:
$$\begin{align*}H(P,Q)&=H(P)+D_{KL}(P||Q) \\&=-E_{\mathsf{x}\sim P}\log Q(x) \\&=-\Sigma P(x)\log Q(x) \\&= -\Sigma PlogP(x)+\Sigma PlogP(x)-\Sigma PlogQ(x) \\&= H(P(x)) +\Sigma PlogP(x)/Q(x) \\&=H(P(x))+D_{KL}(P(x)||Q(x)) \end{align*}$$
针对Q最小化交叉熵等价于最小化KL散度,因为𝐻(𝑃)与Q无关. (也就是交叉熵就是真值分布的熵与KL散度的和,而真值的熵是确定的,与模型的参数Θ无关,所以梯度下降求导时 $∇𝐻(𝑃,𝑄)=∇𝐷_{𝐾𝐿}(𝑃||𝑄)$,也就是说最小化交叉熵与最小化KL散度是一样的)
四. 极大似然估计
机器学习中,通过最大似然估计方法使参数为Θ̂ 的模型使预测值贴近真实数据的概率最大化,即$\hat\Theta=arg\ max_\theta \Pi_{i=1}^Np(x_i|\Theta)$
实际操作中,连乘很容易出现最大值或最小值溢出,造成计算不稳定,由于log函数的单调性,所以将上式进行取对数取负,最小化负对数似然(NLL)的结果与原始式子是一样的,即$\hat \Theta =arg\ min_\Theta - \Sigma_{i=1}^Nlog(p(x_i|\Theta))$
对模型的预测值进行最大似然估计:
$$
\begin{align*}\hat \Theta &=arg\ min_\Theta - \Sigma_{i=1}^Nlog(q(x_i|\Theta)) \\&=arg\min_\Theta-\Sigma_{x\in X}p(x)log(q(x|\Theta)) \\&=arg\ min_\Theta H(p, q) \end{align*}
$$
所以最小化NLL和最小化交叉熵最后达到的效果是一样的
五. MLE–>KL–>CE
由于
$$
E_{\mathsf{x}\sim p_{data}}[\log p_{model}(x)]=\sum_{i=1}^{m}p_{data}\cdot \log p_{model}(x;\theta)
$$
极大似然估计可以经过缩放,用与训练数据经验分布𝑝𝑑𝑎𝑡𝑎相关的期望来表示:
$$\begin{equation}
\theta_{ML}=\mathop{\arg\min}_{\theta}E_{\mathsf{x}\sim p_{data}} \log p_{model}(x^{(i)};\theta)
\end{equation}$$
极大似然估计可以看作最小化训练集熵的经验分布$𝑝_{𝑑𝑎𝑡𝑎}$和模型分布之间的差异,即二者之间的KL散度:
$$D_{KL}(p_{data}||p_{model})=E_{\mathsf{x}\sim p_{data}}\left[ \log p_{data}-\log p_{model}(x) \right]$$
而最小化KL散度又等价于最小化分布之间的交叉熵
$$-E_{\mathsf{x}\sim p_{data}}[\log p_{model}(x)]$$
小结
交叉熵作为神经网络的损失函数的意义:
- 交叉熵刻画的是实际输出(概率)与期望输出(概率)的距离,也就是交叉熵的值越小,两个概率分布就越接近,即拟合的更好
$CrossEntropy=H(p)+D_{KL}(p∣∣q)$
- 当p分布是已知,则熵是常量;于是交叉熵和KL散度则是等价的
最小化KL散度和模型采用最大似然估计进行参数估计又是一致的
这也是很多模型又采用最大似然估计作为损失函数的原因
从优化模型参数角度来说,最小化交叉熵,NLL,KL散度这3种方式对模型参数的更新来说是一样的。从这点来看也解释了为什么在深度学习中交叉熵是非常常用的损失函数的原因了
- https://www.cnblogs.com/jenny1000000/p/7745458.html
- https://blog.csdn.net/elite666/article/details/83850786
- https://www.cnblogs.com/arkenstone/p/10524720.html
- https://www.jianshu.com/p/adf684ceea79
Naive Bayes & MLE
朴素贝叶斯的分类器/目标函数
- 假设给定了一批训练数据
$D = {(x^1,y^1),....,(x^N,y^N)}$- 其中
$x_i$指的是第i个样本(文章),而且这个样本(文章)包含了$m_i$个单词,所以可以把$x_i$表示成$x_i = (x^i_1,x^i_2,...,x^i_{m_i})$ - 用 K 来代表分类的个数
- 用 V 来代表词典库的大小 朴素贝叶斯是生成模型,它的目标是要最大化概率p(D),也就是p(x,y) :
- 其中
$$
\begin{align*}
p(D) &= \prod^N_{i=1} p(x^i,y^i) = \prod^N_{i=1} p(x^i|y^i)p(y^i) \tag{1}
\\&= \prod^N_{i=1} p(x^i_1,x^i_2,...,x^i_{m_i},|y^i)p(y^i) \tag{2}
\\&= \prod^N_{i=1} \prod^{m_i}_{j=1} p(x^i_j|y^i)p(y^i) \tag{3}
\end{align*}
$$
- (1) 通过联合概率得到
- (2) -> (3) 通过条件独立(Conditional Independence)假设得到
- 防止概率连乘引起overflow or underflow, 加上log函数(严格递增):
$$
\begin{align*}
log p(D)
&= log(\prod^N_{i=1} \prod^{m_i}_{j=1} p(x^i_j|y^i)p(y^i)) \tag{4}
\\&= log(\prod^N_{i=1} \prod^{V}_{j=1} p(w_j|y^i)^{n_{ij}} p(y^i)) \tag{5}
\end{align*}
$$
- 从词典库的维度把所有的单词都考虑了进来,并数一下每一个单词在文档i里出现了多少次,如果没有出现,相当于0次
- 其中
$n_{ij}$代表单词j出现在文档i的次数 $w_j$代表词典库里的第j个单词
$$
\begin{align*}
&= \sum^N_{i=1} \sum^{V}_{j=1} n_{ij} log p(w_j|y^i) + \sum^N_{i=1}log p(y^i) \tag{6}
\\&= \sum_{k=1}^K \sum_{i: y^i=k} \sum^{V}_{j=1} n_{ij} log p(w_j|y^i=k) + \sum_{k=1}^K \sum_{i: y^i=k} log p(y^i=k)\tag{7}
\\&= \sum_{k=1}^K \sum_{i: y^i=k} \sum^{V}_{j=1} n_{ij} log \theta_{kj} + \sum_{k=1}^K \sum_{i: y^i=k} log \pi_k \tag{8}
\\&= \sum_{k=1}^K \sum_{i: y^i=k} \sum^{V}_{j=1} n_{ij} log \theta_{kj} + \sum_{k=1}^K n_k log \pi_k \tag{9}
\end{align*}
$$
- (6) -> (7) 把文档按照类别做了一个分类. 现在先取出类别为1的文档, 然后再取出类别为2的文档, 以此类推.
$\sum^N_{i=1}$被拆分成两个sum, 即$\sum_{k=1}^K \sum_{i: y^i=k}$$i: y^i=k$代表属于类别k的所有文档
- (7) -> (8) 引入了两组变量. 直接设置
$w_j|y^i=k$为$\theta_{kj}$意思就是当文章分类为k的时候出现单词$w_j$的概率($\theta_{kj}$). 另外,设定$p(y^i=k)$为$\pi_k$,也就是文档属于第k类的概率,这个也是朴素贝叶斯模型的先验(prior) - (8) -> (9) 引入一个新的变量叫做
$n_k$, 也就是属类别k的文件个数(训练数据总统计即可,是已知的), 即$\sum_{i: y^i=k}\pi_k = n_k\pi_k$
另外, 有两个约束条件需要满足, 分别是:
$$
\begin{align*}
\sum_{u=1}^K \pi_u = 1 \tag{10}
\\ \sum_{v=1}^V \theta_{kv} = 1, for \; k=1,2,...,K \tag{11}
\end{align*}
$$
- 条件(10)表示的是所有类别的概率加在一起等于1
- 条件(11)表示的是对于任意一个分类k出现所有词典里的单词的总概率合为1
利用拉格朗日乘法项, 可以把目标函数写成:
$Maximize \; L = \sum_{k=1}^K \sum_{i: y^i=k} \sum^{V}_{j=1} n_{ij} log \theta_{kj} + \sum_{k=1}^K n_k log \pi_k + \lambda(\sum_{u=1}^K \pi_u - 1) + \sum^K_{k=1} \lambda_k (\sum_{v=1}^V \theta_{kv} - 1) \tag{12}$
朴素贝叶斯的参数估计( by MLE )
设置导数为0, 进而找出最优解.
找出最优解$\pi_k$:
L对$\pi_k$的导数为:
$$
\begin{align*}
\frac{\delta L}{\delta \pi_k} &= \frac{\delta (n_k log \pi_k + \lambda \pi_k)}{\delta \pi_k}
\\ &=\frac{n_k}{\pi_k} + \lambda = 0
\end{align*}
$$
解为$\pi_k = -\frac{1}{\lambda}n_k$. 这里有个参数λ,但同时有一个约束条件是$\sum_{u=1}^K \pi_u = 1$, 把刚才的解带入到这里, 可以得到:
$$\sum_{u=1}^K -\frac{1}{\lambda}n_u = 1$$
则λ的值为$\lambda = - \sum^K_{u=1} n_u$. 把λ再次带入到$\pi_k$里面, 可以得到:
$$\pi_k = - \frac{n_k}{\sum^K_{u=1} \pi_u}$$
这里面$n_k$为k类文档出现的个数, 分母为所有文档的个数.
找出最优解$\theta_{kj}$:
L对$\theta_{kj}$的导数为:
$$
\begin{align*}
\frac{\delta L}{\delta \theta_{kj}} &= \frac{\delta (\sum_{i: y^i=k} n_{ij} log \theta_{kj}) + \lambda_k (\sum_{v=1}^V \theta_{kv} - 1)}{\delta \theta_{kj}}
\\ &=\sum_{i:y^i = k} \frac{n_ij}{\theta_{kj}} + \lambda_k = 0
\end{align*}
$$
解为$\theta_{kj} = -\frac{1}{\lambda_k} \sum_{i: y^i=k} n_{ij}$. 这里有个参数是$\lambda_k$, 但同时有个约束条件$\sum_{v=1}^V \theta_{kv} = 1$. 把刚才的解带入到这里, 可以得到:
$$\lambda_k = -\frac{1}{\sum^V_{v=1}\sum_{i: y^i=k} n_{iv}}$$
把$\lambda_k$带入到上面的解即可以得到:
$$\theta_{kj} = \frac{\sum_{i: y^i=k} n_{ij} }{\sum^V_{v=1}\sum_{i: y^i=k} n_{iv}}$$
这个式子中分子代表的是在所有类别为k的文档里出现了多少次$w_j$也就是词典库里的j个单词. 分母代表的是在类别为k的所有文档里包含了总共多少个单词.
Evaluation of Classifier
准确率(accuracy) 不适合样本不平衡的时候
精确率(precision): % of selected items(in prediction) that are correct(in ground truth)
召回率(recall): % of correct items(in ground truth) that are selected (in prediction)
R & P 互斥.So need P > threshold & R > threshold
f1-score: 平衡了R & P
$\frac{2*precision * recall}{precision + recall}$

Logistic Regression
可以把逻辑回归当做baseline
- 逻辑回归:
$y = \frac{1}{1+e^{-x}}$ - 原始条件概率:
$P(Y|X) = w^Tx + b$ - 新条件概率:
$y = \frac{1}{1+e^{-w^Tx + b}}$
对于二分类问题:
$p(y=1|x,w) = \frac{1}{1+e^{-w^Tx + b}}$$p(y=0|x,w) = \frac{e^{-w^Tx + b}}{1+e^{-w^Tx + b}} = 1 - p(y=1|x,w)$
两个式子合并: $p(y|x,w) = p(y=1|x,w)^y[1-p(y=1|x,w)]^{1-y}$
逻辑回归是一个线性的分类器(linear classifier)
- 通过决策边界(descision boundry)去判断是线性还是非线性
- The decision boundary is the line that separates the area where y = 0 and where y = 1
- 逻辑回归的决策边界:
- 因为落在逻辑回归的决策边界两边的概率是相同的
- 所以
$\frac{p(y=1|x,w)}{p(y=0|x,w)} = 1$ $e^{-w^Tx + b} = 1$$log (e^{-w^Tx + b}) = log 1$$w^Tx + b = 0$<== 逻辑回归的决策边界
逻辑回归的目标函数(objective function)
- 定义了
$p(y|x,w) = p(y=1|x,w,b)^y[1-p(y=1|x,w,b)]^{1-y}$ - 需要最大化目标函数:
$w^*_{MLE},b^*_{MLE} = argmax_{w,b} \prod_{i=1}^n p(y_i|x_i,w,b)$$w^*_{MLE},b^*_{MLE} = argmax_{w,b} log(\prod_{i=1}^n p(y_i|x_i,w,b))$$w^*_{MLE},b^*_{MLE} = argmax_{w,b} \sum_{i=1}^n log p(y_i|x_i,w,b)$$w^*_{MLE},b^*_{MLE} = argmin_{w,b} - \sum_{i=1}^n log p(y_i|x_i,w,b)$$w^*_{MLE},b^*_{MLE} = argmin_{w,b} - \sum_{i=1}^n log [p(y_i=1|x_i,w,b)^{y_i}[1-p(y_i=1|x_i,w,b)]^{1-y_i}]$$w^*_{MLE},b^*_{MLE} = argmin_{w,b} - \sum_{i=1}^n y_i \cdot log[p(y_i=1|x_i,w,b)]+(1-y_i)\cdot log[1-p(y_i=1|x_i,w,b)]$
梯度下降法
求使得f(w)值最小的参数w
通过优化算法求出来的是解是全局最优解还是局部最优(Global Optimal Vs Local Optimal)
- 是否凸函数(convex function)
- 凸函数的解一定是全局最优解
- 判断: 二阶导数都大于等于0
- 非凸函数 – 神经网络
- 凸函数的解一定是全局最优解
- 最优化算法
- 最简单 f’(w) = 0 ===> w = ?
- Iterative
- GD
- SGD
- Adagrad
- Adam
- …


随机梯度下降法

在GD中, 为了更新一个梯度, 需要循环所有的样本.
在SGD中, 每次的更新只依赖其中一个样本的梯度
- 但是每次计算出啦的梯度存在一定噪声
Regularization
- Q: 当给定的数据线性可分的时候, 逻辑回归的参数会趋向于正无穷大, 为什么?
- A: 因为
$ P = \frac{1}{1+e^-z}$, 当z越大的时候, P越趋向于1; 因为$z = w^Tx+b$, 所以w将会变得非常大(趋向于正无穷大), 而形成过拟合的现象
防止参数w过大的解决方法 – 正则化
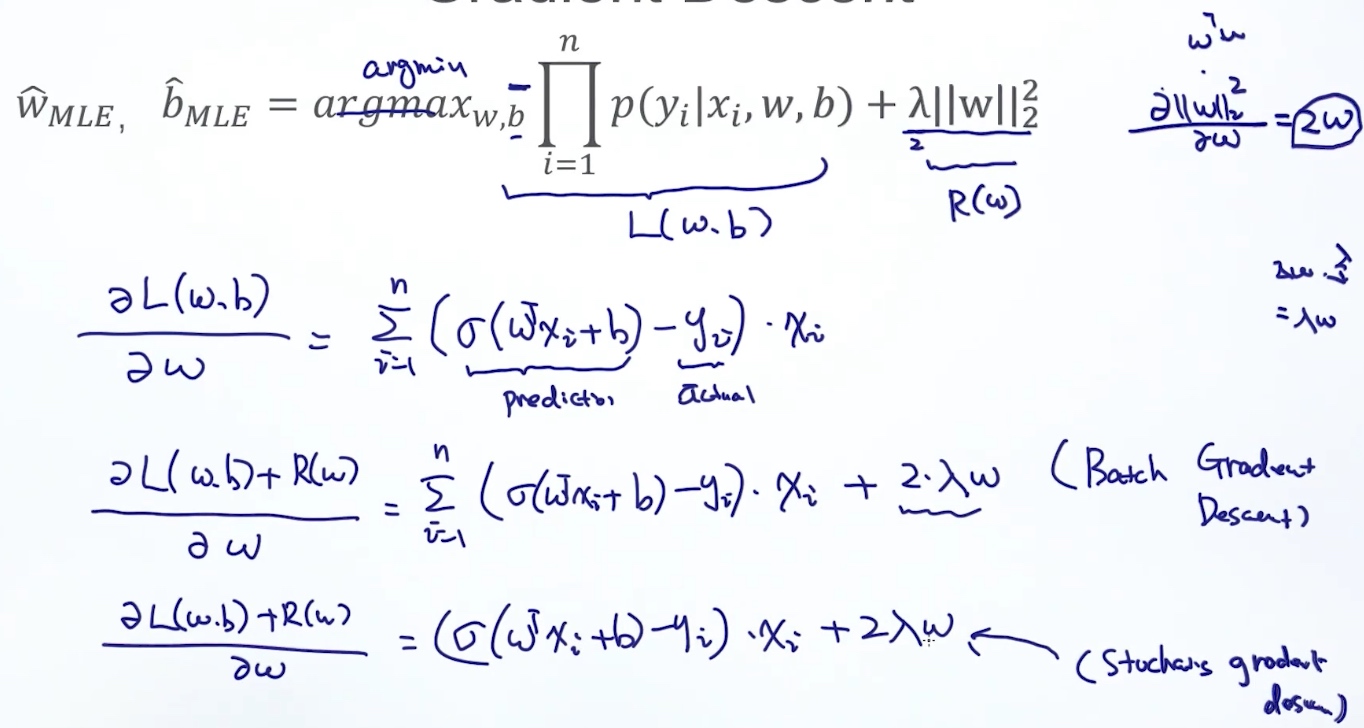
模型复杂度
过拟合与欠拟合
模型泛化能力
解决过拟合的方法:
- 选择不同的模型
- 减少模型参数的个数
- 模型的参数空间选择 (通过正则的方式去过滤掉不需要的区间)
- 由于模型拟合过少的样本, 所以增加样本
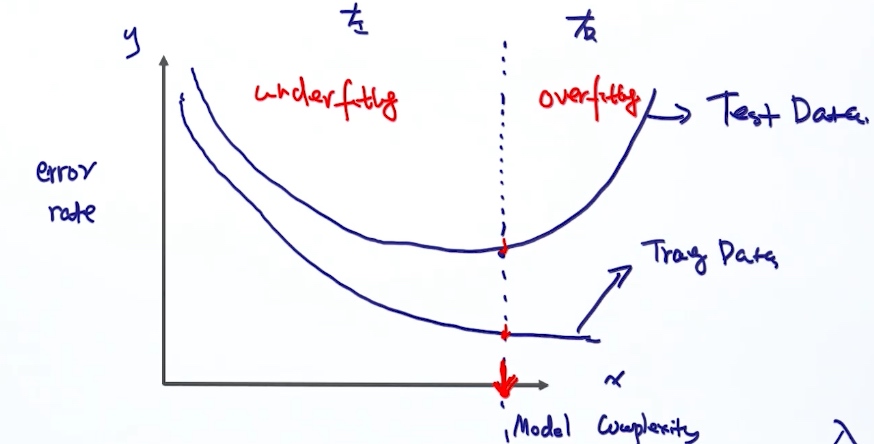
L1 VS L2
L1-Norm
L2-Norm
L1,L2 regularized Objective function
$argmin \; f(\theta) + \lambda||\theta ||^2_2$$argmin \; f(\theta) + \lambda||\theta ||_1$
| L1 | L2 | |
|---|---|---|
| make θ smaller | ✓ | |
| induce sparse solution | ✓ | ✘ |
sparse solution 代表有些θ会等于0
Geometric Interpretation of L1 vs L2
几何角度的解释
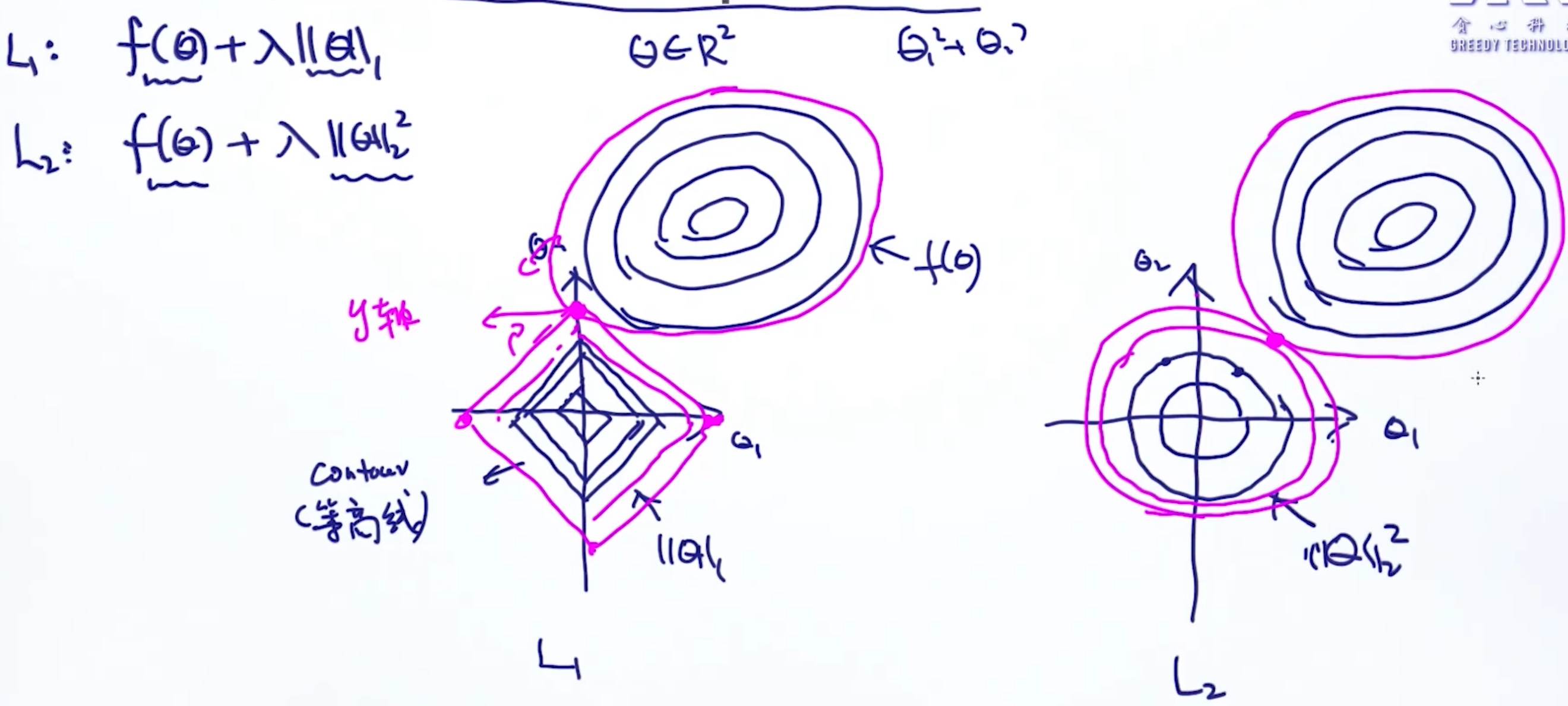 L1中有些参数为0 是因为L1范数的形状, 类似正方形/菱形, 一个菱形和另一个函数的交集时, 这个交集很可能发生在菱形的顶点上
L1中有些参数为0 是因为L1范数的形状, 类似正方形/菱形, 一个菱形和另一个函数的交集时, 这个交集很可能发生在菱形的顶点上
Use both L1, L2
ElesticNet: $argmin \; f(\theta) + \lambda_1||\theta ||_1 + \lambda_2||\theta ||^2_2$
正则的高级应用
Neuro-Science

Cross-Validation
帮助选择超参数 cv = 5:
| Train | Train | Train | Train | Val |
|---|---|---|---|---|
| Train | Train | Train | Val | Train |
| Train | Train | Val | Train | Train |
| Train | Val | Train | Train | Train |
| Val | Train | Train | Train | Train |
将选择的超参数每个验证集中应用, 得到一个准确率; 最终算出5个准确率的平均值, 然后进行下一个超参数; 对比, 选择平均准确率最高的那个超参数
参数搜索策略
- Grid Search
- for loop遍历所有超参数, 得到不同的Candidate set并逐个放入CV
- Random Search 随机搜索
- Genetic/Evolutionary Algorithm 遗传算法
- 量化 (因子)
- Bayesian Optimization 贝叶斯优化
- 类似遗传算法, 在好的解的周围可能也存在好的解
深度学习十分多超参数:
应用auto ML, 以智能的方式去搜索参数, 在最短时间内得到结构最优的神经网络
MLE & MAP
最大似然估计 - 估计参数仅仅依赖对样本的观测值
- ‘H,H,H,T,T,H’
- MLE: p(正面) = 2⁄3
最大后验估计 - 估计参数依赖对样本的观测值和先验概率(专家的经验)
- ‘H,H,H,T,T,H’
- prior: 0.8 硬币主人说它正面的概率
- MLE: p(正面) = 2⁄3
- 所以MAP: 在 67.7% ~ 80% 之间
先验概率的重要性随着样本个数的增加而减少
Mathematical Formulation
MLE:
$$arg\max P(D|\theta)$$
MAP: MAP其实就是在最大化贝叶斯定理
$$
\begin{align*}
arg\max P(\theta|D)
&= arg\max \frac{P(D|\theta)\cdot P(\theta)}{P(D)}
\\&= arg\max P(D|\theta)\cdot P(\theta)
\end{align*}
$$
MAP 比 MLE多了一个先验概率
From Gaussian Prior to L2 Regularization
MLE:
$$
\begin{align*}
arg\max P(D|\theta)
&= arg\max \prod^n_{i=1} P(y_i|x_i;w)
\\ &= arg\max \sum^n_{i=1} log P(y_i|x_i;w)
\end{align*}
$$
MAP:
$$
\begin{align*}
arg\max P(\theta|D)
&= arg\max P(D|\theta) \cdot P(\theta)
\\ &= arg\max log P(D|\theta) + log P(\theta)
\\ &= arg\max \sum^n_{i=1} log P(y_i|x_i;w) + logP(\theta)
\end{align*}
$$
Given that
假设期望值$\mu = 0$
$$
\begin{align*}
P(\theta) &= P(w) \sim N(0,\sigma^2)
\\P(w) &= \frac{1}{\sqrt{2\pi}\sigma}exp(\frac{w^2}{2\sigma^2})
\\log P(w) &= log( \frac{1}{\sqrt{2\pi}\sigma}exp(\frac{w^2}{2\sigma^2}))
\\ &=-log(\sqrt{2\pi}\sigma) - \frac{w^2}{2\sigma^2}
\end{align*}
$$
MAP:
$$
\begin{align*}
arg\max P(\theta|D)
&= arg\max \sum^n_{i=1} log P(y_i|x_i;w) + logP(\theta)
\\ &= arg\max \sum^n_{i=1} log P(y_i|x_i;w) -log(\sqrt{2\pi}\sigma) - \frac{w^2}{2\sigma^2}
\\ &= arg\max \sum^n_{i=1} log P(y_i|x_i;w) - \frac{1}{2\sigma^2} ||w||^2_F
\end{align*}
$$
- 其中, $-log(\sqrt{2\pi}\sigma)$为常数项, 不会造成影响, 所以直接去掉
- $\frac{1}{2\sigma^2}$ 就相当于 $\lambda$
From Laplace Prior to L1 Regularization
MLE:
$$
\begin{align*}
arg\max P(D|\theta)
&= arg\max \prod^n_{i=1} P(y_i|x_i;w)
\\ &= arg\max \sum^n_{i=1} log P(y_i|x_i;w)
\end{align*}
$$
MAP:
$$
\begin{align*}
arg\max P(\theta|D)
&= arg\max P(D|\theta) \cdot P(\theta)
\\ &= arg\max log P(D|\theta) + log P(\theta)
\\ &= arg\max \sum^n_{i=1} log P(y_i|x_i;w) + logP(\theta)
\end{align*}
$$
Given that
假设期望值$\mu = 0$
$$
\begin{align*}
P(\theta) &= P(w) \sim Laplace(0,b)
\\P(w) &= \frac{1}{2b}exp(-\frac{|x|}{b})
\\log P(w) &= log( \frac{1}{2b}exp(-\frac{|x|}{b}))
\\ &=log(\frac{1}{2b}) - \frac{|x|}{b}
\end{align*}
$$
MAP:
$$
\begin{align*}
arg\max P(\theta|D)
&= arg\max \sum^n_{i=1} log P(y_i|x_i;w) - \frac{1}{b} ||w||_1
\end{align*}
$$
- 其中, $log(\frac{1}{2b})$为常数项, 不会造成影响, 所以直接去掉
- $\frac{1}{b}$ 就相当于 $\lambda$
总结:
- MLE & MAP的区别就是 MAP 比 MLE多了一个先验概率P(θ); 也可以反过来,认为MLE是把先验概率P(θ)认为等于1,即认为θ是均匀分布
- 且 加了一个先验概率就等于做了正则化
- Gaussian Prior ==> L2 Reg
- Laplace Prior ==> L1 Reg
- 当数据非常多的时候, MAP solution –> MLE Solution
- 因为MAP中 MLE的部分是相加, 会越来越大, 先验起到作用就被淡化
MAP,MLE & Bayesian
- 贝叶斯估计是最大后验估计的进一步扩展,贝叶斯估计同样假定
$\theta$是一个随机变量,但贝叶斯估计并不是直接估计出$\theta$的某个特定值,而是估计$\theta$的分布 - https://zhuanlan.zhihu.com/p/37215276
- https://www.jianshu.com/p/9c153d82ba2d
Lasso & Ridge Regression)
Ridge = Linear Regression + L2 Reg $L = ||Xw - y||^2_F + \lambda||w||^2_2$
Lasso = Linear Regression + L1 Reg $L = ||Xw - y||^2_F + \lambda||w||_1$
Lasso特点:
- 在 N < D (特征数小于维度)时候, 特别有效
- 由于加了L1 Reg, 拥有稀疏性的特征, 起到特征选择的功能, 把无用的特征权重设为0
Why prefer Sparsity
- 如果维度太高, 计算量也变得很高
- 在稀疏性条件下, 计算量只依赖非0项的个数
- 提高可解释性
特征选择的方法
- Exhaustive Search
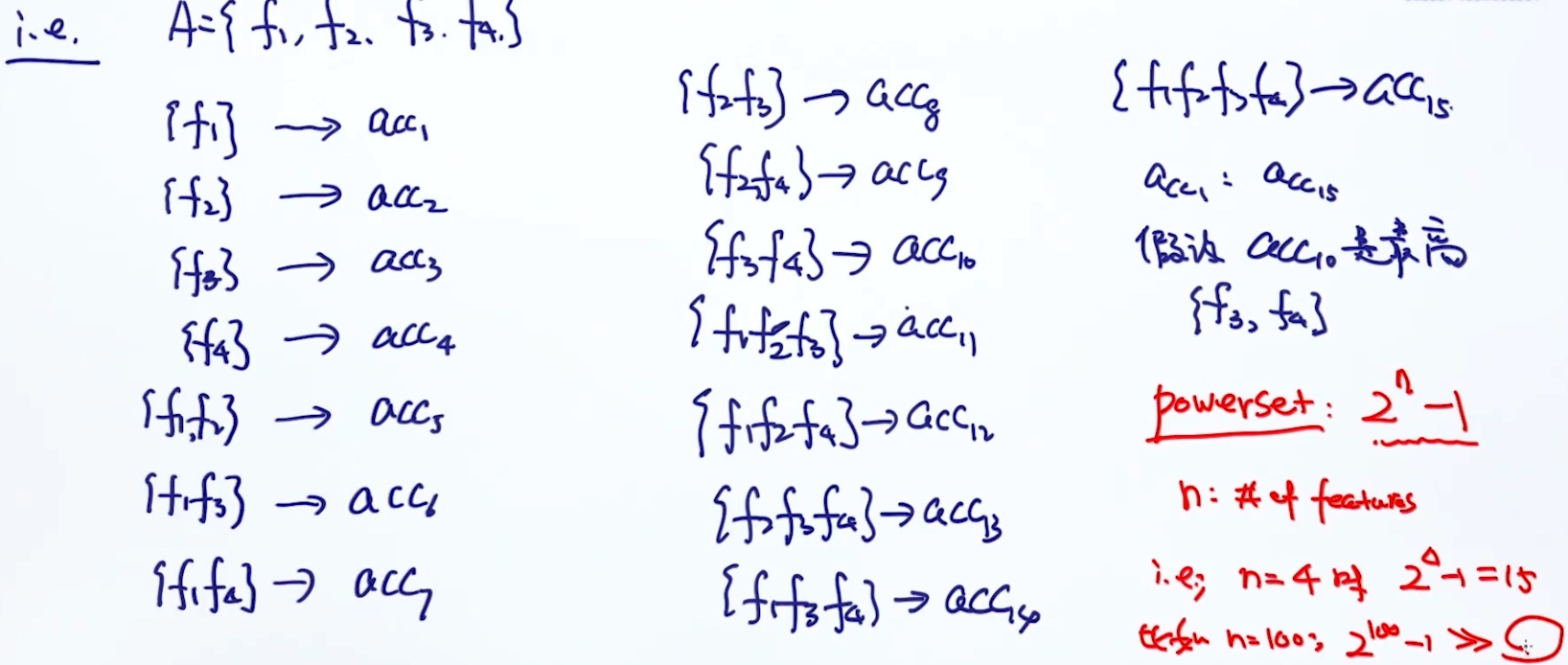
- 列举所有特征的组合, 以此判断哪个组合的准确率最高
- 指数级的复杂度
- Greedy Approach
- Forward Stepwise
- Backward Stepwise
- Forward Stepwise
- Via Regularization (LASSO)
优化LASSO 目标函数
$L = ||Xw - y||^2_F + \lambda||w||_1 \\ ||w||_1 = |w_1|+|w_2|+...|w_n|$
但是针对L1正则求导($|w_j|$对$w_j$的梯度)要考虑3种情况: $\frac{\delta |w_j|}{\delta w_j}$
$w_j > 0$时, 梯度为1$w_j < 0$时, 梯度为-1$w_j = 0$时, 梯度不是唯一的
所以不考虑使用gradient descent; 转而使用Coordinate Descent.
Coordinate Descent (LASSO Solver)
核心思想: 函数有多个维度, 在求解最优解的时候, 每次只考虑其中一个维度(最优解在摸一个维度上), 这时, 其他维度可以当成常数项.
Goal: minimize function g:
$g(w) = g(w_1,w_2,...,w_D)$- 循环
- 在t=1时刻,
$\hat{w_1} = arg\min_{w_1} g(w_1)$- 然后使
$g(w_1)$的导数为0 , 就可以求出最优$w_1$
- 然后使
- 在t=2时刻,
$\hat{w_2} = arg\min_{w_2} g(w_2)$- 使
$g(w_2)$的导数为0 , 求出最优$w_2$
- 使
- …
- 在t=1时刻,
comments:
- 选择下一个coordinate:
- 依次选择 w1,w2,…,wD,w1,w2,…
- 随机选择 w6,w3,w54,w2,w22,…
- 不需要设定step-size(learning rate)
- 对于lasso objective, 它会收敛
Coordinate Descent for LASSO

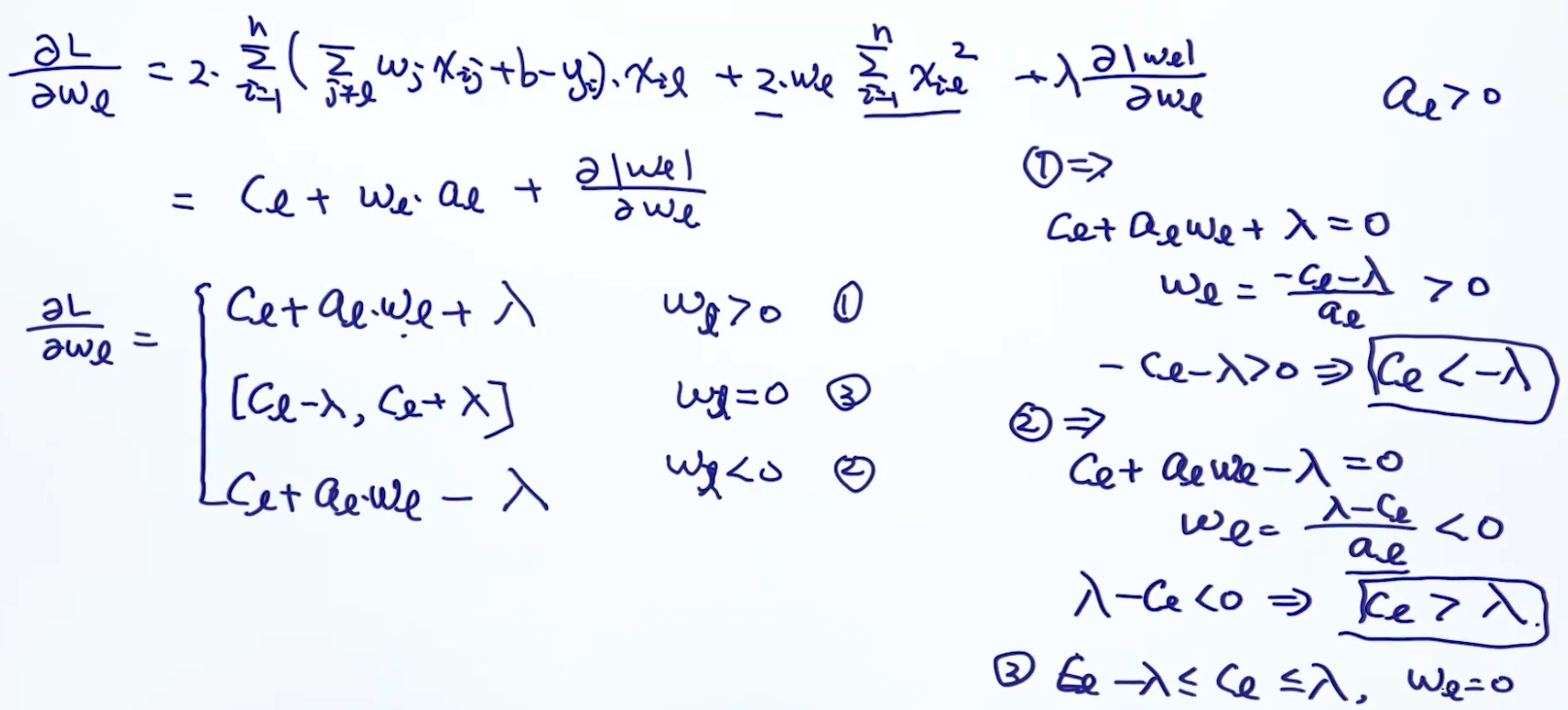
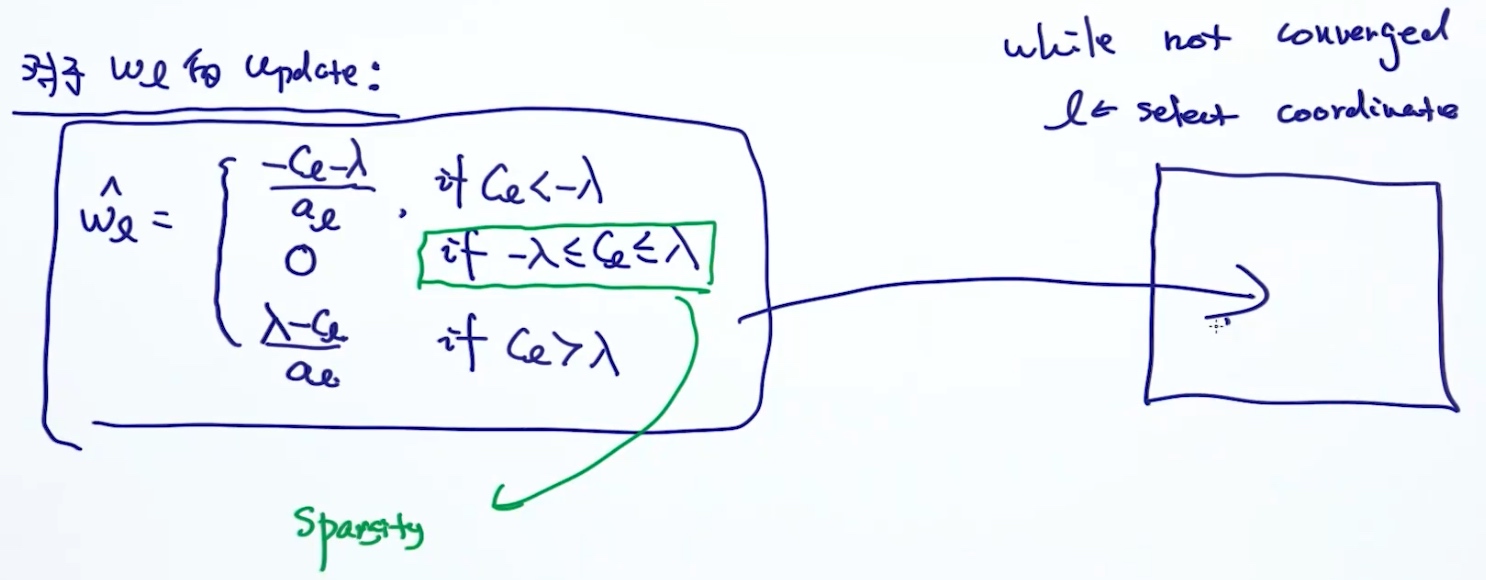
Other LASSO Solver
- Least angle regress (LARS)
- Parallel CD (shotgun)
- Parallel SGD
- Parallel independent solutions then averaging
- Alternating directions method of multipliers (ADMM)
凸优化
AI问题 = 模型 + 优化
任何一个问题, 都可以协程如下形式:
$$
Minimize f(x)
\\ s.t. f_i(x) \leq 0, \;\;i={1,...,K}
\\ g_i(x) = 0, \;\;j={1,...,L}
$$
例子:
- 线性回归
$minimize_w ||Xw-y||^2_F$ - 逻辑回归
$minimize_{w,b} =\sum^n_{i=1}y_ilog(\sigma(w^Tx_i+b)) +(1-y_i)og[1-\sigma(w^Tx_i+b)] +\lambda||w||^2_2$ - SVM
$||w||^2 +c\sum^n_{i=1} \epsilon_i \;\;\;\; s.t. \epsilon \geq 1-y_ix_i^Tw,\;\; \epsilon_i \geq 0$ - Collaborative Filtering
- K-means
$minimize_{\mu_1,...,\mu_k} \sum^K_{j=1}\sum^n_{i=1} ||x_i^{(j)} - \mu_j||^2$ - portfolio optimization

Optimization - Categories
- smooth VS non-smooth
- non-smooth (LASSO)
- convex VS non-convex
- global optimal VS local optimal
- local optimal (深度学习) -> 初始化变得十分重要 -> multiple/better initialization (pre-training)
- discrete VD continuous
- discrete optimization (Relaxation)
- constrained VS non-constrained
Convex Optimization: global optimal VS local optimal
凸函数
回顾:
$f(x) = 2x+2$- 定义域:
$x \in R^n$ - 值域:
$f(x) \in R^n$
判断凸函数
- f(x)的定义域是凸集
- 凸集(convex set): 假设对于任意
$x,y \in C$并且任意参数,$\alpha \in [0,1]$, 有$\alpha x + (1-\alpha)y \in C$, 则集合为凸集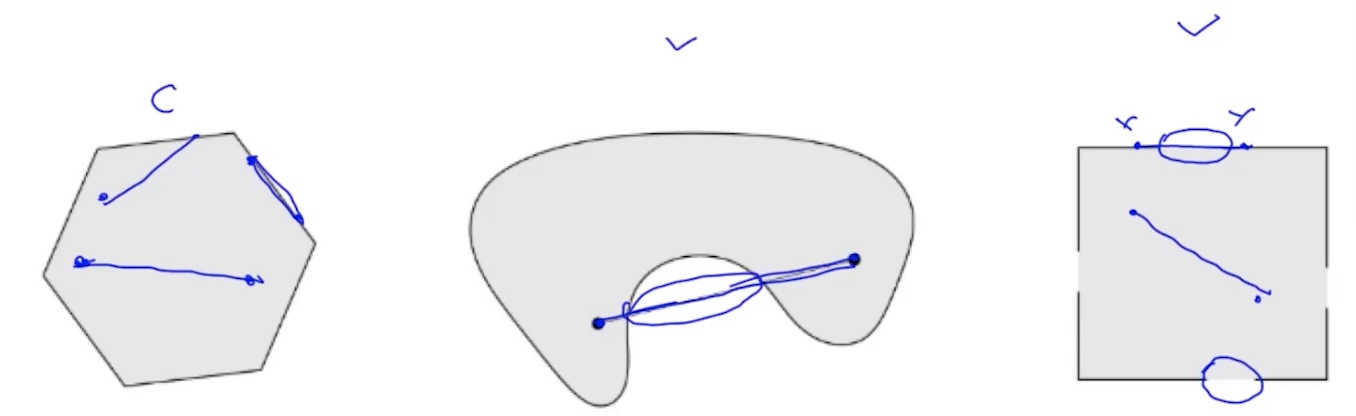
- 例子:
- 所有的
$R^n$ - 所有正数集合
$R^n_+$ - 范数
$||x|| \leq 1$ - Affine set: 线性方程组的所有解
$Ax = b$ - Halfspace: 不等式的所有解:
$Ax \leq b$
- 所有的
- 两个凸集的交集也是凸集
- 凸集(convex set): 假设对于任意
- 函数满足
$f(\theta x + (1-\theta)y) \leq \theta f(x) + (1-\theta)f(y), \;\; \theta \in [0,1]$ - 例子:
- 线性函数为凸/凹函数
- exp x, -logx, xlogx
- 范数
$\frac{x^tx}{t}, \;\; x>0$
- 其他判别方法: First Order Convexity Condition
- 假设
$R^n -> R$是可导的, 则f为凸函数, 当且仅当$f(v) \geq f(x) + \delta(x)^T(y-x)$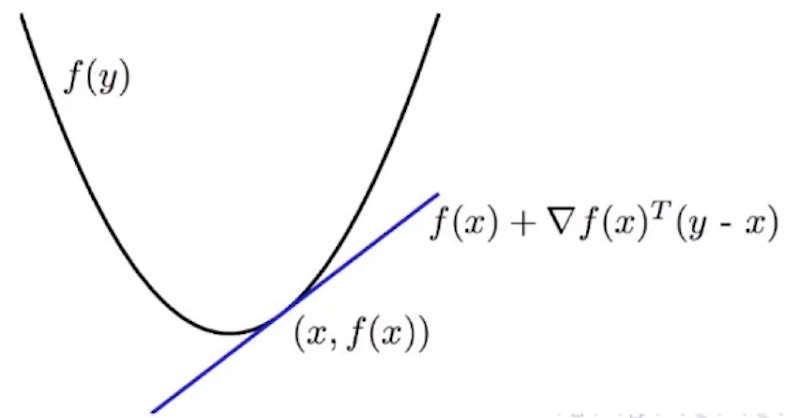
- 假设
- 其他判别方法: Second Order Convexity Condition
- 假设
$R^n -> R$是两次可导的, 则f为凸函数, 当且仅当$\delta^2f(x) \geq 0$
- 假设
线性函数: $f(x) = b^Tx+c$
假设$x_1,x_2 => \\ f(x_1)=b^Tx_1+c, \\ f(x_2)=b^Tx_2+c$
则:
$$
b^T(\theta x_1 +(1-\theta)x_2)+c \leq \theta(b^Tx_1+c) + (1-\theta)(b^Tx_2+c) \\
\theta b^Tx_1+(1-\theta)b^Tx_2+c \leq \theta b^Tx_1+ \theta c + (1-\theta)b^Tx_2+(1-\theta)c \\
c \leq \theta c + (1-\theta)c \\
c leq c
$$
所以f(x)是凸函数
二次方函数 $f(x) = \frac{1}{2}x^TAx + b^Tx+c$ 对于任意$A\geq 0$ (说明了A是正定矩阵)
$$
\frac{\delta f(x)}{\delta x} = Ax + b \\
\frac{\delta^2 f(x)}{\delta^2 x} = A
$$
因为A是正定矩阵, 所以f(x)是凸函数
L1 / L2范数
$||\theta x_1 + (1-\theta)x_2|| \leq \theta ||x_1||+(1-\theta)||x_2 ||$
Maximun Flow Problem
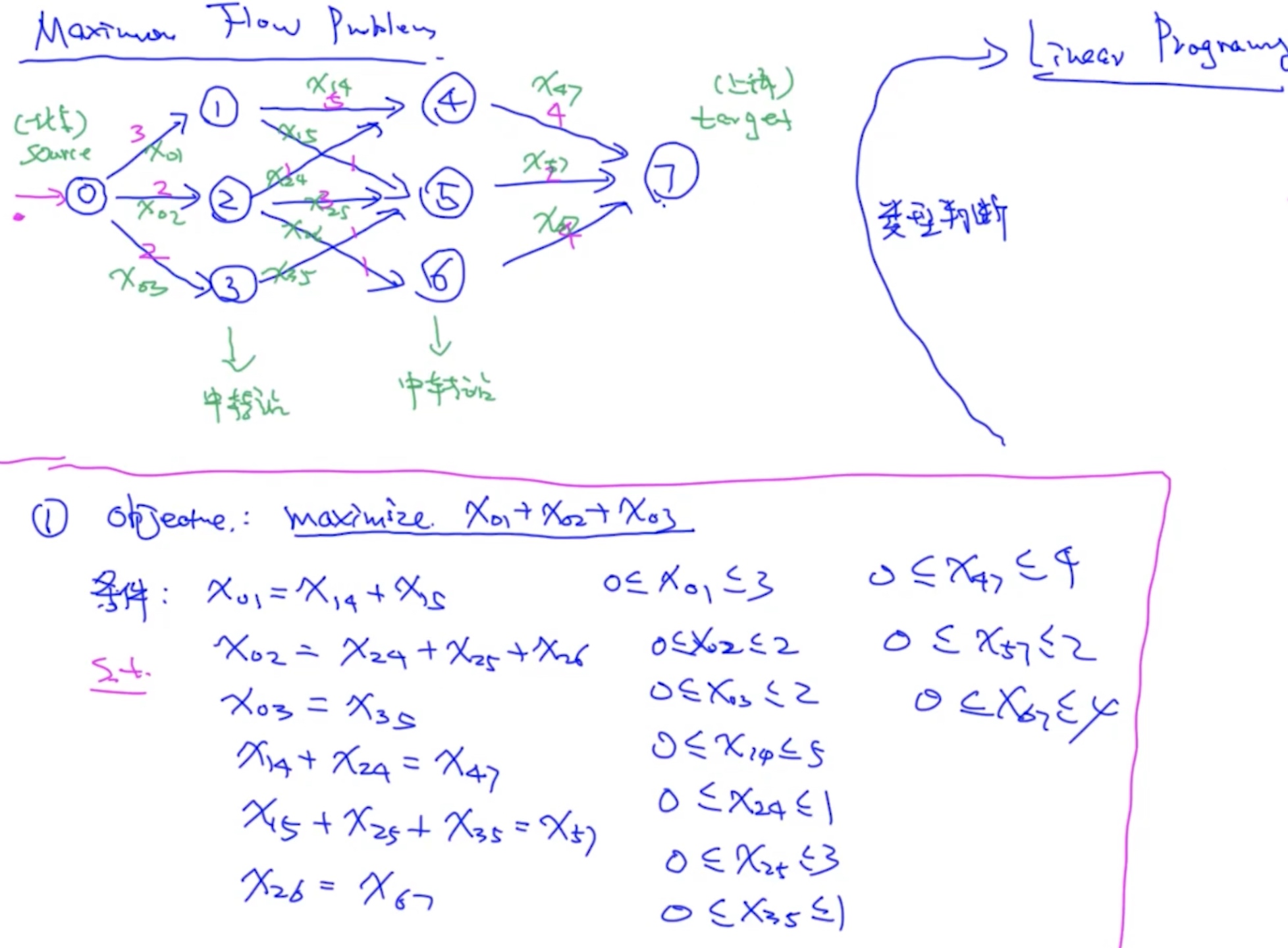 https://docs.scipy.org/doc/scipy/reference/generated/scipy.optimize.linprog.html
https://docs.scipy.org/doc/scipy/reference/generated/scipy.optimize.linprog.html

Set Cover Problem
假设有个全集U(Universal Set), 以及m个子集合S1,S2,…,Sm, 目标是要寻找最少个数的集合, 使得集合union等U
例子: U = {1,2,3,4,5}, S:{S1={1,2,3}.S2={2,4},S3={1,3},S4={4},S5={3,4},S6={4,5}}, 最少的集合为{1,2,3},{4,5}, 集合个数为2
- Exhaustive Search
- 列举所有可能的集合, 时间复杂度高, 但可以找到全局最优解
- Greedy Search
- 每次循环排除可以删掉的集合,时间复杂度不高, 不能保证全局最优解
- Optimization

Integer Linear Programming:
$$
\begin{align*}
minimize \sum^m_{i=1} x_i \tag{Linear} \\
s.t. \sum_{i:e\in S_i} x_i \geq 1 \tag{Linear}\\
x_i \in {0,1} \;\;\; i=1,...,m \tag{Integer(discrete)}
\end{align*}
$$
Non-Convex Function: 因为$\alpha x_1 +(1-\alpha)x_2 \in {0,1}$ 而根据定义, 它不是 $\in [0,1]$, 所有它的定义域不是凸集
Relaxation
$$
\begin{align*}
minimize \sum^m_{i=1} x_i \\
s.t. \sum_{i:e\in S_i} x_i \geq 1 \\
x_i \in [0,1] \;\;\; i=1,...,m \tag{DIFFERENCE}
\end{align*}
$$
由discrete转到continuous, 加上条件限制:
if xi < 0.5, xi=0
if xi >= 0.5, xi=1SVM
对于第(1),(3)条决策边界, 离边界近的点, 可能加点噪点(pertubation), 就会被错误分类, 不够robust.
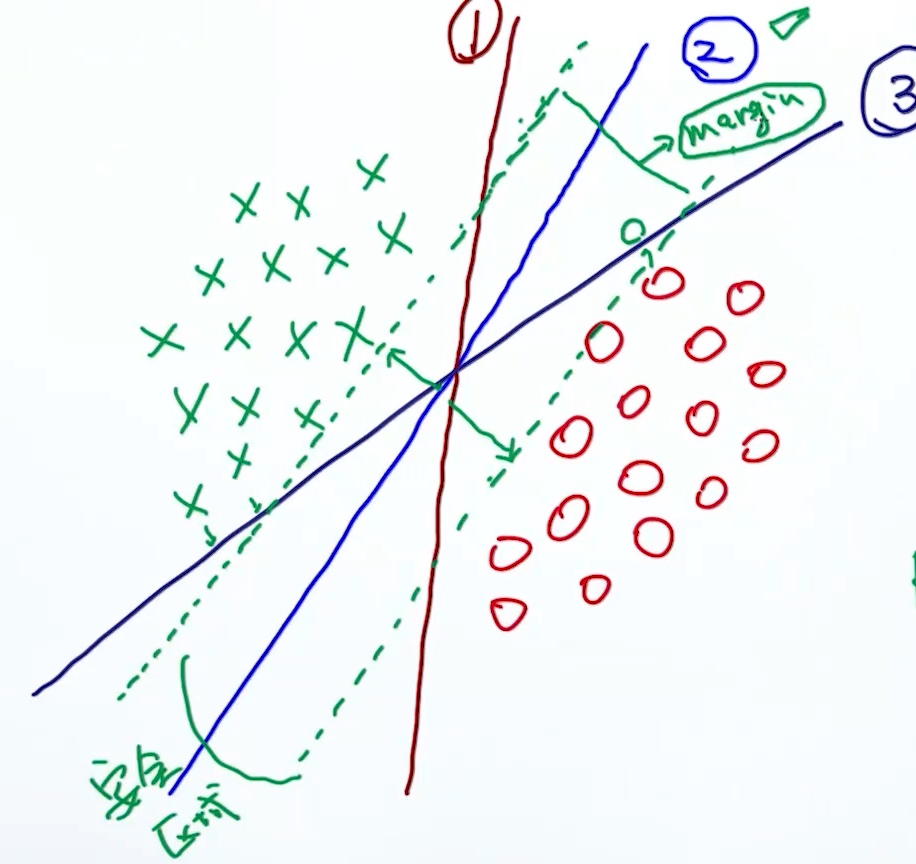 对于第(2)条决策边界, 它是最好的, 因为它的安全区域/margin足够大, robust to perturbation. 所以SVM就是一个Max-Margin Method.
对于第(2)条决策边界, 它是最好的, 因为它的安全区域/margin足够大, robust to perturbation. 所以SVM就是一个Max-Margin Method.
Maximize the Margin
 图中, w 垂直于
图中, w 垂直于 $w^Tx+b = 0$这条线, 证明:
$wx_1+b=0, \;\;\; wx_2+b=0$$w(x_1-w_2)=0$$w \perp (w_1-x_2) $因为 斜率不存在时直线与x轴垂直, 斜率为0时直线与x轴平行
在$w^Tx+b=1, \;\;\; w^Tx+b=-1$ 这两条线上各取一点 $x_+, x_-$, 求margin
$$
\begin{align}
\left\{
\begin{array}{**lr**}
w^Tx_++b=1 & [1] \\ \tag{1}
w^Tx_-+b=-1 & [2] \\
x_+ = x_- +\lambda w & 因为x_+,x_-都在w的方向 & [3]
\end{array}
\right.
\end{align}
$$
margin就是$x_+, x_-$的距离
$$
\begin{equation}
margin = |x_+ - x_-|
\end{equation}
$$
$$
\begin{align*}
w^T(x_- +\lambda w)+b=1 \tag{3} \\
w^Tx_- +\lambda w^T w+b=1 \tag{4}\\
\lambda w^T w - 1 =1 \tag{5}\\
\lambda w^T w =2 \tag{6}\\
\lambda =\frac{2}{w^T w } \tag{7}\\
\end{align*}
$$
- 将(1)中的[3]带入(1)中的[1]得到(3)
- 将(1)中的[2]带入(4)得到(5)
最后:
$$
\begin{align*}
margin &= |\lambda w| \tag{8} \\
&= \lambda ||w|| \tag{9}\\
&= \frac{2}{w^T w } ||w|| \tag{10}\\
&= \frac{2}{||w||} \tag{11}\\
\end{align*}
$$
- 将(1)中的[3]带入(2)得到(8)
- 将(7)带入(9)得到(10)
- w是列向量, 列向量的转置乘以列向量, 就变成向量各个元素的平方之和, 最终得到(11)
Hard Constraint
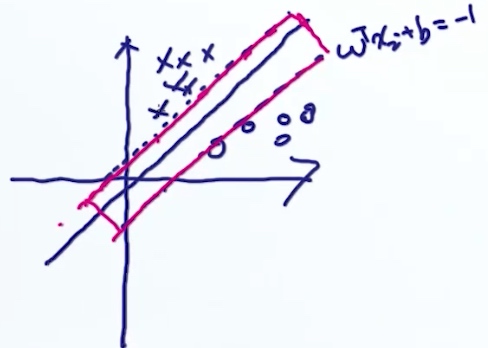
$$
\begin{align*}
& Maximize \frac{2}{||w||} \;==>\; Minimize ||w||^2\\
& s.t. \\
& w^tx_i+b \geq 1 \;\;\; if\;\; y_i=1 \\
& w^tx_i+b \leq 1 \;\;\; if\;\; y_i=-1 \\
\end{align*}
$$
Soft Constraint
 hard-constraint 容易过拟合
hard-constraint 容易过拟合
- soft-constraint容忍错误, 在目标函数上加一个对epsilon的惩罚项
- 从hard到soft的转变就是 由 1 变成 1-epsilon, epsilon>=0
- epsilon相当于允许犯错的空间
Hinge Loss
Convert to hinge loss
 👆Linear SVM
👆Linear SVM
- 约束可以转换成epsilon >= 1-(wx+b)yi
- 由于是最小化目标函数, 所以epsilon取最小值, 即1-(wx+b)yi
- 又因为epsilon>=0, 所以1-(wx+b)yi>=0
- 所以有了hinge loss ==> max(0,1-(wx+b)yi)
SGD for hinge loss

多了一个判断 1-(wx+b)yi 是否小于0
Prime dual
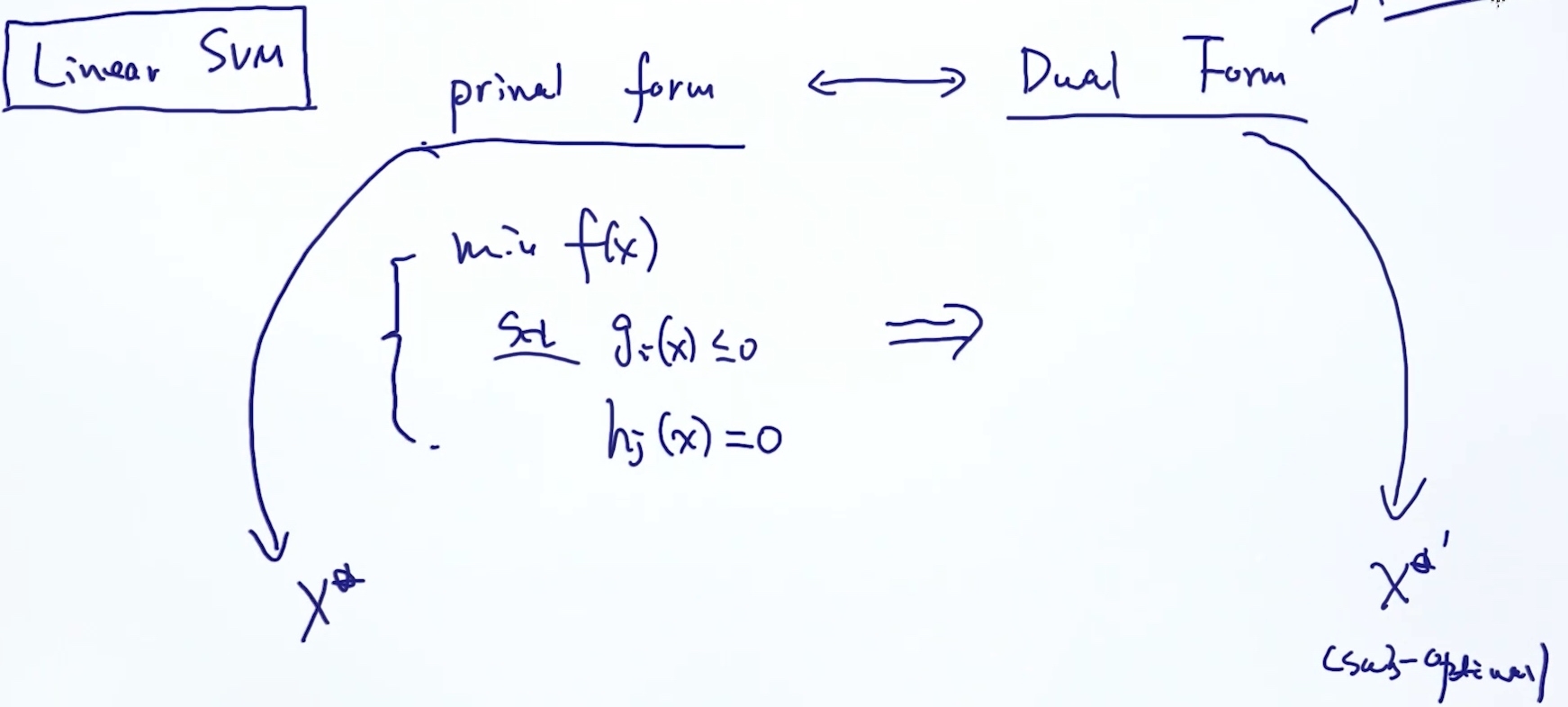 转换成dual form的原因:
转换成dual form的原因:
- 在prime form上找不到最优解, 但是可能会在dual form上找到 最优解 或者是 sub-optimal
- 转换成dual form后容易使用Kernel trick (把数据映射到高维度, 但是使用kernel trick, 相当于计算原始空间的复杂度)
Linear SVM的缺点:
- 解决不了非线性的问题
解决方法:
- 利用非线性模型 - neural network
- 把数据映射到高维空间(在高维空间, 区别度更加明显, 所以可能一个线性模型即可区分开数据), 然后学习一个线性模型
Mapping feature to High Dimensional Space
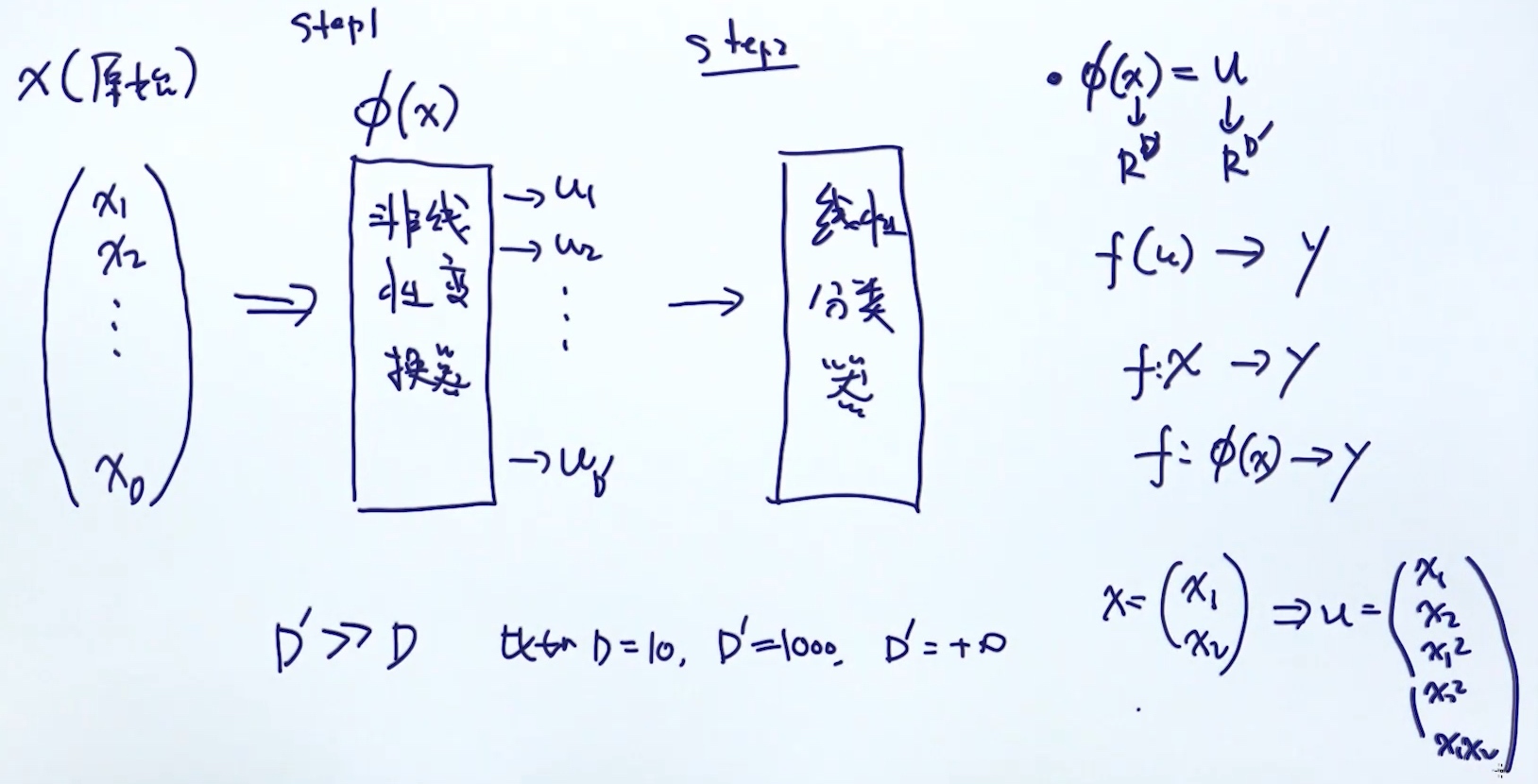 缺点:
缺点:
- 转为高维, 时间复杂度增加
- 构建模型的复杂度增加 O(D) => O(D`)
- 解决方法: kernel trick (step1和step2的结合)
拉格朗日: 等号条件处理
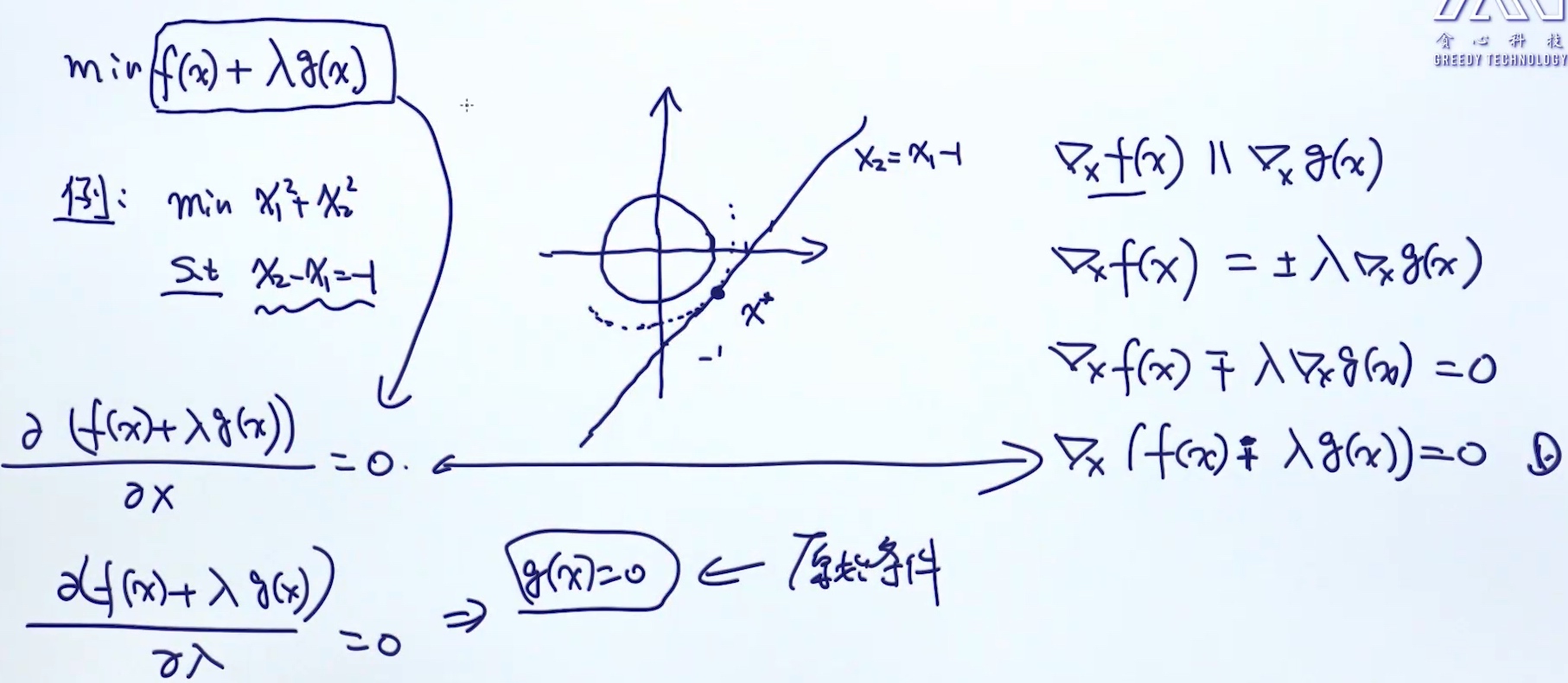
泛化:
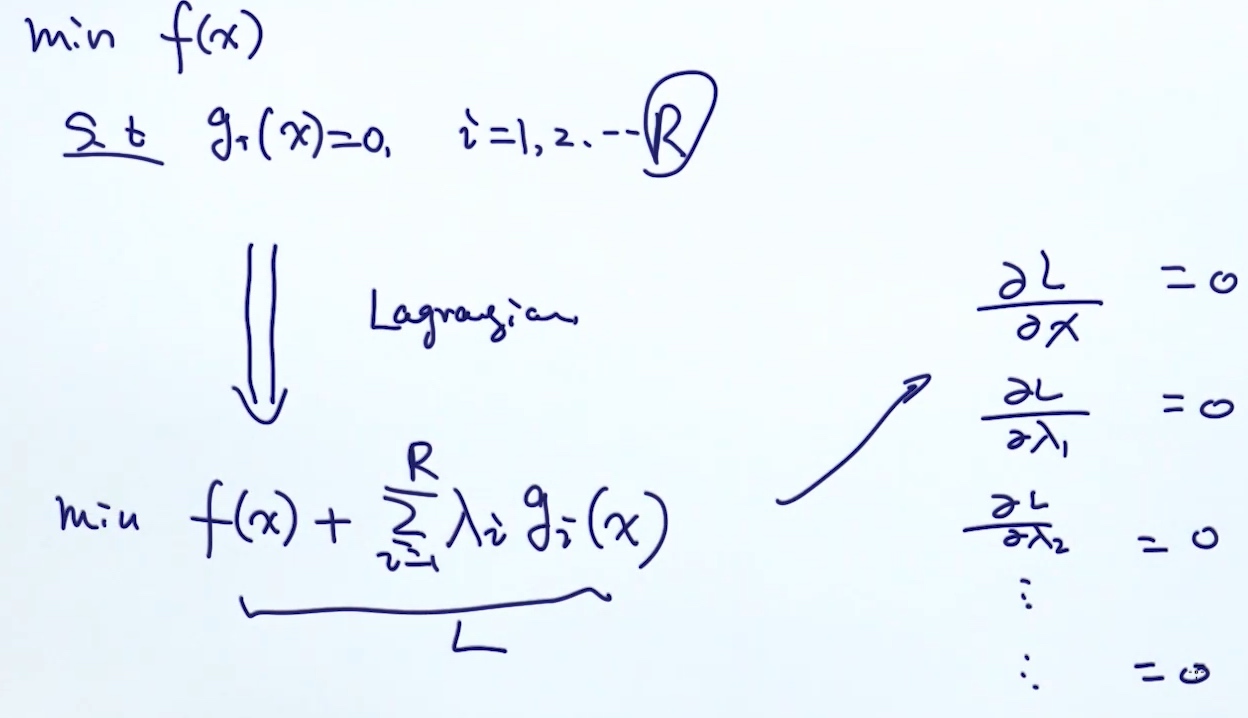
拉格朗日: 不等号条件处理
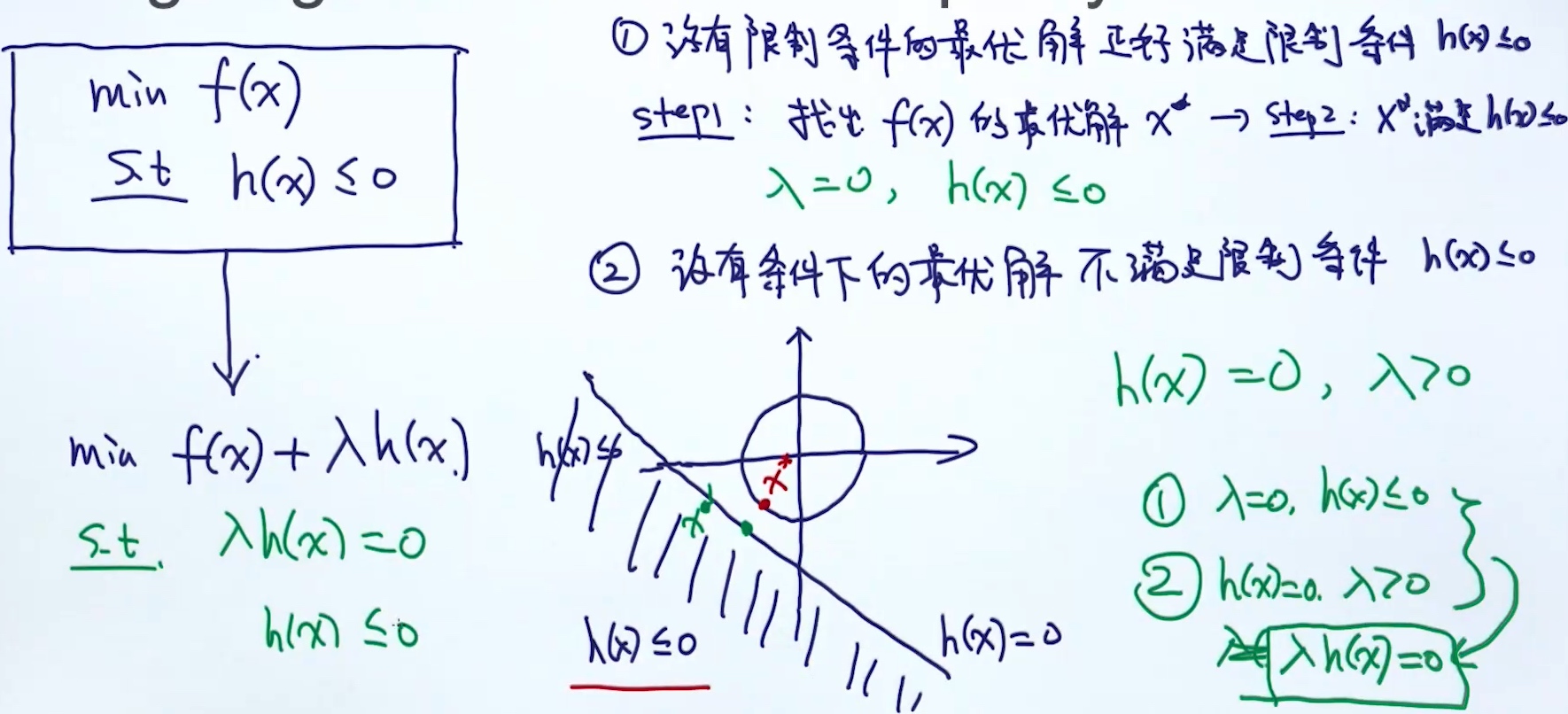
KKT条件
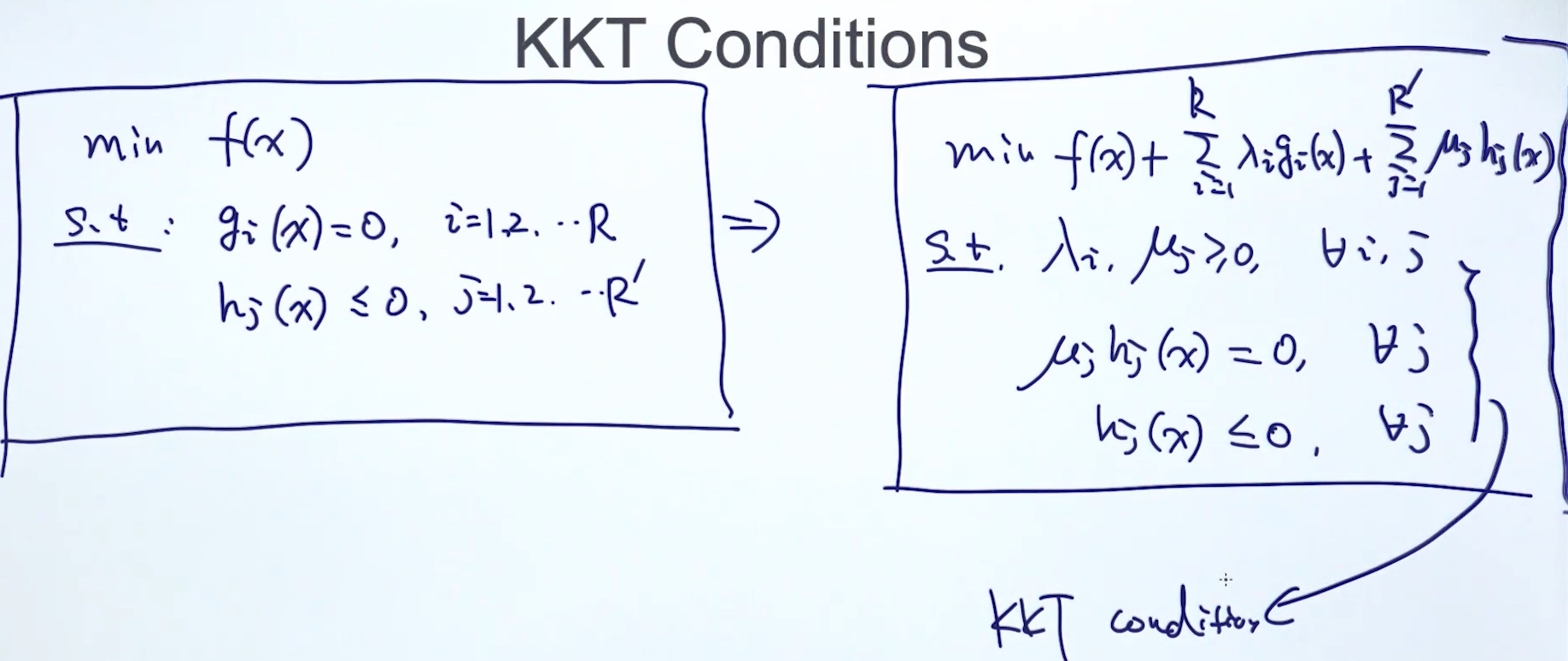
KKT condition of SVM
 👆prime problem
👆prime problem
转换成dual problem的理由
- prime问题有可能比较难解决
- 在dual问题上发下一些有趣的insight (SVM使用kernel trick)
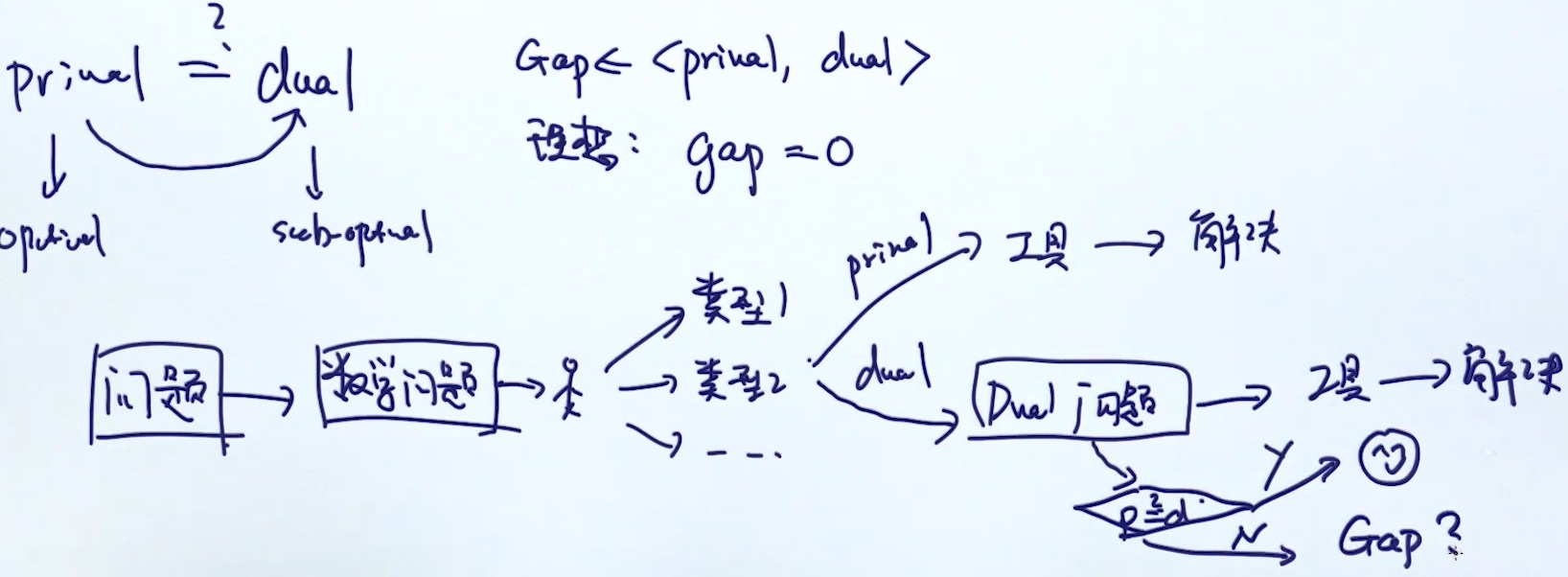
👇dual problem

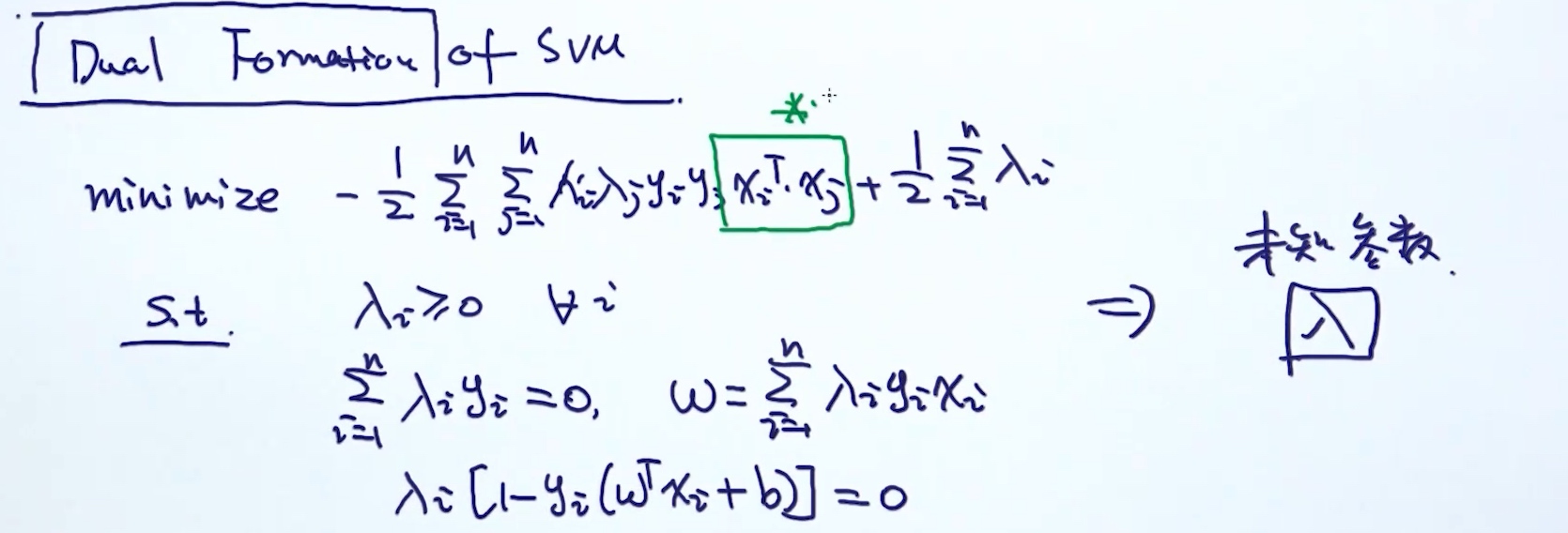
Kernel Trick
现象: 原本空间映射到高维空间后, 仅依赖原本空间内积的运算, 不依赖高维空间的计算
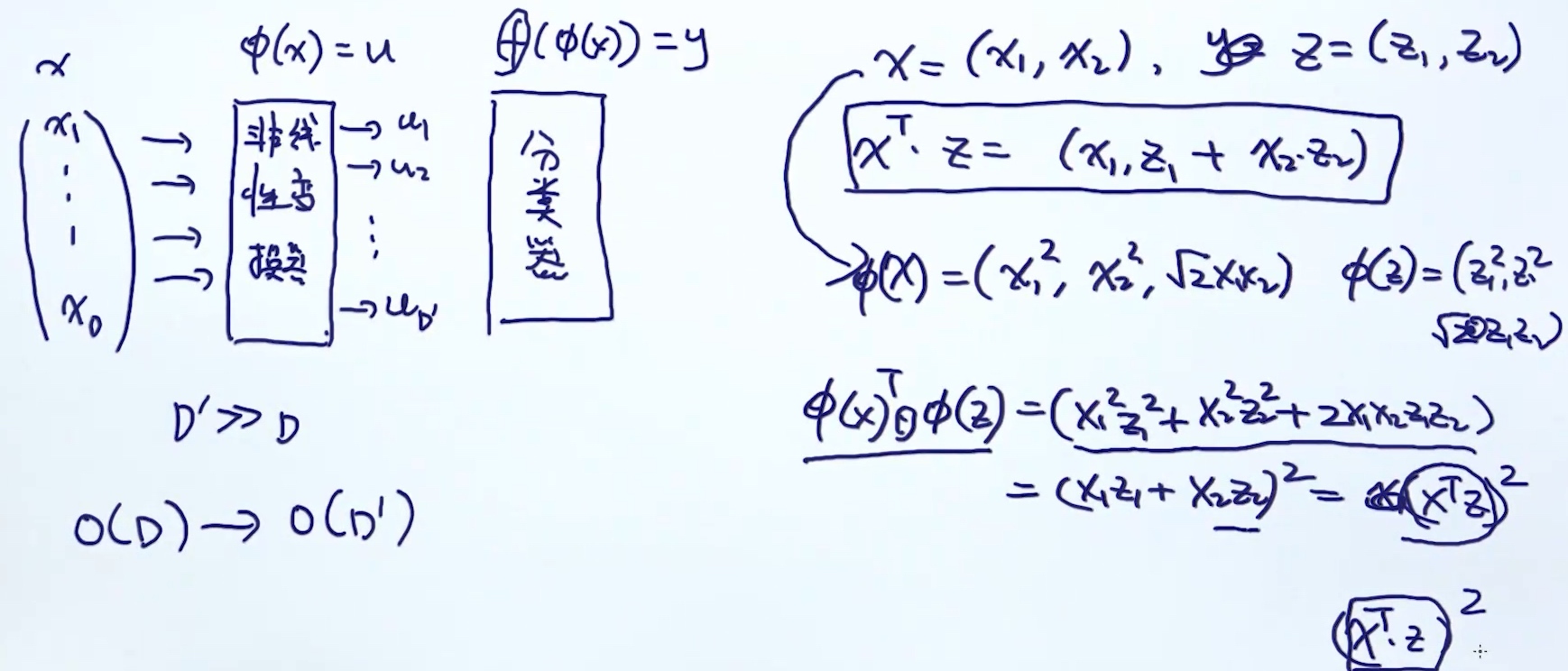
核心: 如何设计非线性变换器$\phi(x)$, 使得内积的计算的时间复杂度保持不变. 又称核函数
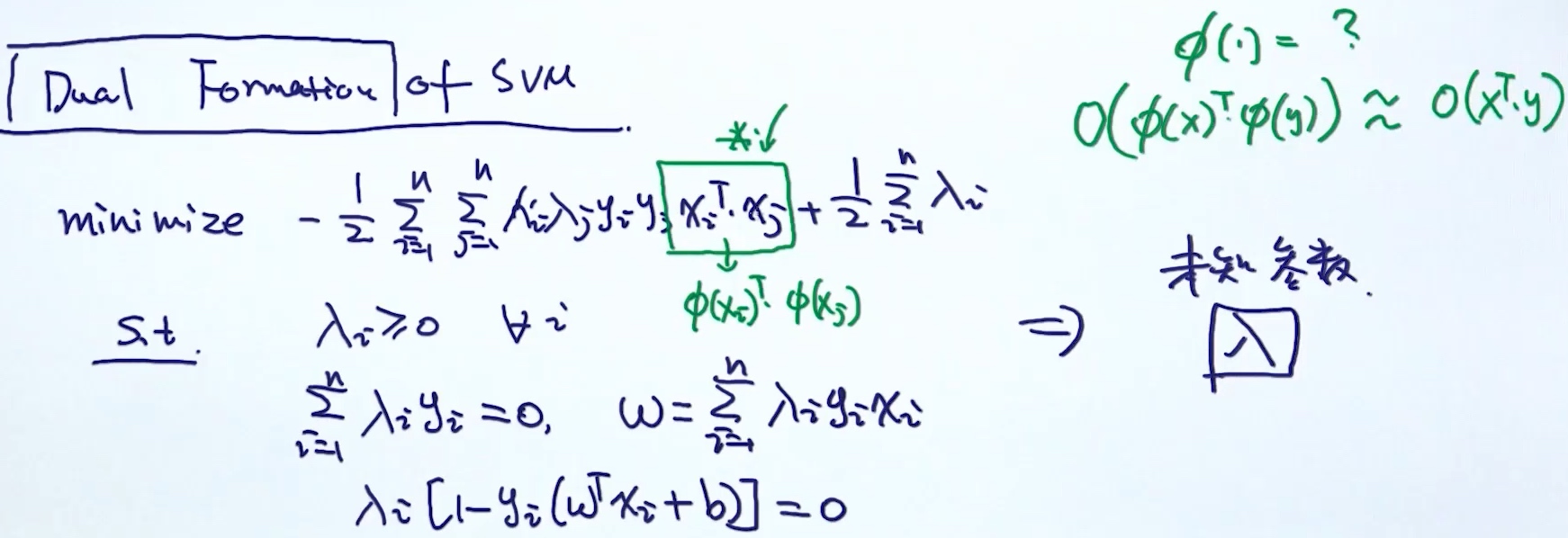 kernel trick 不仅仅是针对SVM, 只要目标函数有内积的计算(dot product)
kernel trick 不仅仅是针对SVM, 只要目标函数有内积的计算(dot product)
Linear Kernel: $K(x,y) = x^T \cdot y$ => linear SVM
Polynomial Kernel: $K(x,y) = (1+x^T \cdot y)^d$
Guassian Kernel: $K(x,y) = exp(\frac{-||x-y||^2}{2 \sigma^2})$
Mercer’s Theorem
Python高阶函数的应用
Lambda
匿名函数
add_lambda = lambda x,y:x+y
add_lambda(3,4)
# output: 7三元运算符
condition = True
print(1 if condition else 2)
# output: 1Map
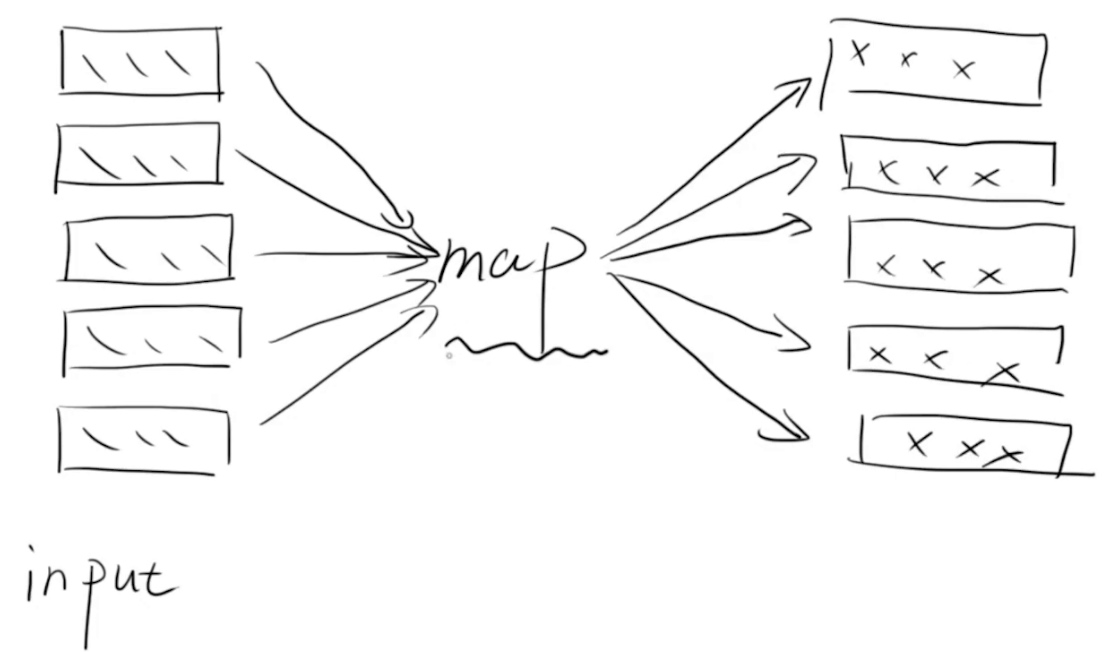
list1 = [1,2,3,4,5]
r = map(lambda x:x+x, list1)
print(list(r))
# output: [2,4,6,8,10]list1 = [1,2,3,4,5]
r = map(lambda x,y:x*x+y, list1,list1)
print(list(r))
# output: [2,6,12,20,30]Filter
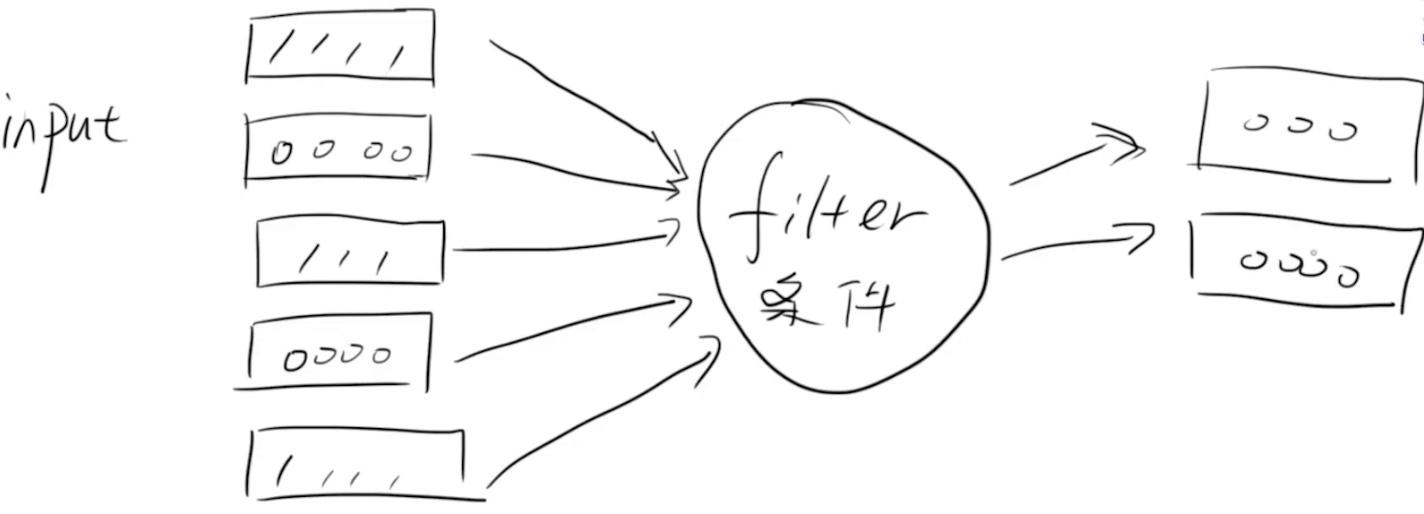
def is_not_None(s):
return s and len(s.strip()) > 0
list1 = ['',' ','hello',None,'ai']
r = filter(is_not_None, list1)
print(list(r))
# output: ['hello','ai']Reduce
for functools import reduce
add_lambda = lambda x,y:x+y
list1 = [1,2,3,4,5]
r = reduce(add_lambda, list1)
print(r)
# output: 15列表推导式
list1 = [1,2,3,4,5]
r = [i*i for i in list1]
print(r)
# output: [1,4,9,16,25]# 有选择性的筛选
list1 = [1,2,3,4,5]
r = [i*i for i in list1 if i>3]
print(r)
# output: [16,25]集合推导式
list1 = [1,2,3,4,5]
r = {i*i for i in list1}
print(r)
# output: {1,4,9,16,25}# 有选择性的筛选
list1 = [1,2,3,4,5]
r = {i*i for i in list1 if i>3}
print(r)
# output: {16,25}字典推导式
dic = {'alan':12,'charon':2,'bb':3}
r = [k+'aa' for k,v in dic.items()]
print(r)
# output: ['alanaa','charonaa','bbaa']# key,value颠倒
dic = {'alan':12,'charon':2,'bb':3}
r = {v:k for k,v in dic.items()}
print(r)
# output: {12:'alan',2:'charon',3:'bb'}# 只拿出符号条件的值
dic = {'alan':12,'charon':2,'bb':3}
r = {v:k for k,v in dic.items() if k == 'bb'}
print(r)
# output: {3:'bb'}闭包
一个返回值是函数的函数
import time
def runtime():
def get_time():
print(time.time())
return get_time
f = runtime()
f()
# output: 1590393945.343486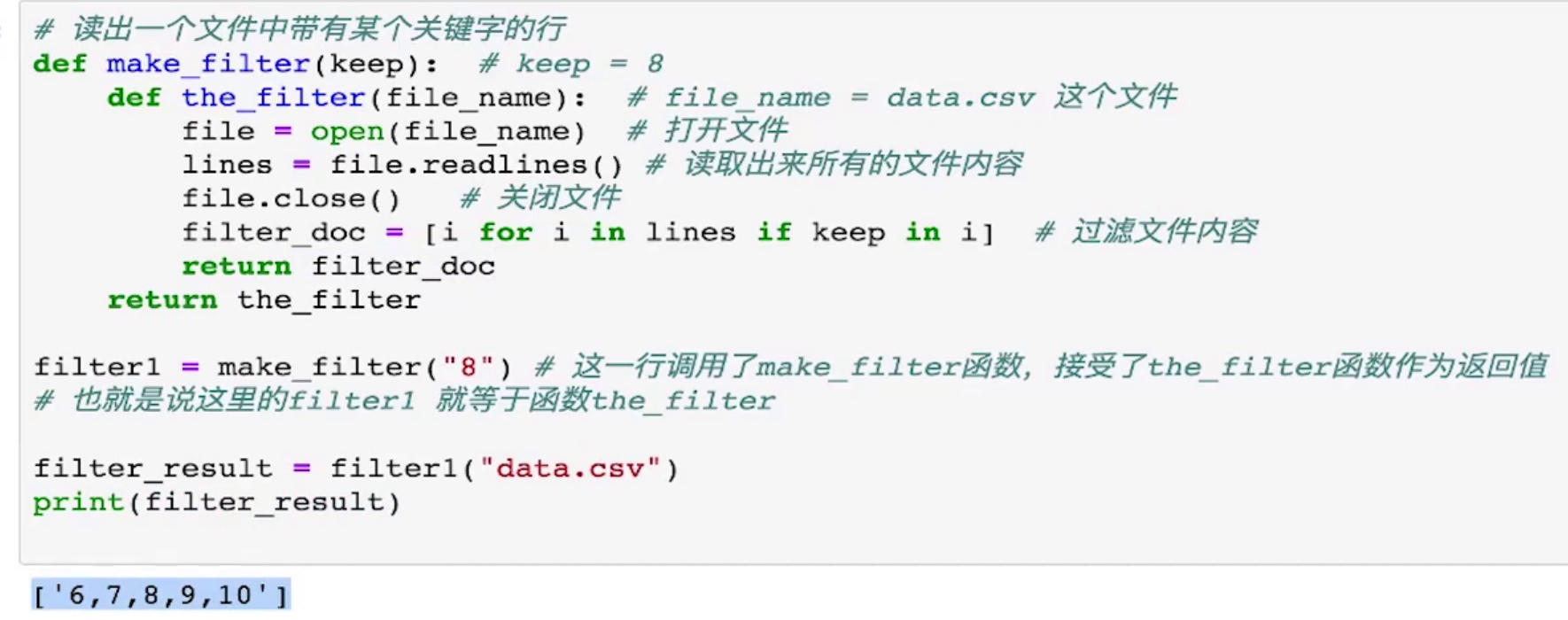
装饰器
又称: 语法糖 / 注解
import time
def runtime(func):
def get_time(*args):
func(*args)
print(time.time())
return get_time
@runtime
def f(i,j):
print('start')
f(1,2)
# output:
# start
# 1590393945.343486import time
def runtime(func):
def get_time(*args,**kwargs):
func(*args,**kwargs)
print(time.time())
return get_time
@runtime
def f(*args,**kwargs):
print('start')
f(8,i=1,j=5)
# output:
# start
# 1590393945.343486Numpy
Pandas
Matplotlib
Scrapy
面试
自我介绍
不在简历上
面试要点
- 发展史
- 难点: 词义消歧, 指代消解, 上下文理解, 语义与语用不对等
- 应用: 医疗,教育,媒体,金融,法律,… (根据面试公司)
- 常见工具: 基本工具包,分词, ML框架,DL框架 tensorflow, keras, pytorch,…
- NLP + ML:
- Logistic Regression, Naive Bayes, K-means, SVM, decision tree + 优点缺点
- 集成方法
- NLP + DL:
- CNN, RNN, LSTM, attention, transformer, bert,…
- NLP基本任务
- 文本预处理
- 文本获取 (著名数据集)
- 流程 (词干提取,词性标注,…)
- 数据不平衡的处理 (数据合成…)
- 文本的表示
- tf-idf
- word2vec: CBOW, Skip-gram (原理,训练技巧)
- fasttext, glove,elmo,…
- 句子方面的向量:
- sif
- 序列标注 (NER, pos-tagging, …)
- 基于概率模型的方法: HMM, MEMM, CRF (原理,差别和优缺点)
- 基于DL的方法: Bi-LSTM + CRF
- 关系抽取(做知识图谱,rule-based): Boostrap, DL的方法
- 文本预处理
- 文本聚类
- 方法: 划分法, 层次法, 基于密度, 基于网格
- 应用场景: 数据整理, 数据挖掘, 用户画像, 数据可视化
- 评估方法
- 文本分类
- 方法: ML, 模型融合, DL
- 应用场景: 二分类, 多分类, 多标签
- 评估方法
- 文本摘要
- 方法: 抽取式的, 压缩式的, 重组法
- 应用场景
- 评估方法
- 语言生成
- 方法: 语言模型(基于概率), DL
- 应用场景: 娱乐(写诗机器人), 聊天任务(rule-based)
- 评估方法
- 机器翻译
- 发展史
- 方法: encoder-decoder + attention, self-attention, bert
- 评估方法
- 聊天系统
- 类型: 闲聊, 知识问答, 任务型(多轮对话)
- 任务型: 意图识别, 词槽填充, 对话管理(rule-based,DL,强化学习), 数据库(知识图谱), 对话生成, 强化学习
问题种类
- 常规(技术)问题(上面)
- 项目问题
- 应用场景: 讲出思路解决问题
- 私人信息
如何选择公司
- 人员
- 项目
- 领域+ NLP (不推荐)
- 专业NLP,然后转卖 (要了解进度和投资背景)
- 工作强度