CS224n Week3
Lecture 05 Linguistic Structure: Dependency Parsing
syntactic structure
对于句法结构(syntactic structure)分析,主要有两种方式:
- Constituency Parsing
- Constituency = phrase structure grammar = context-free grammars (CFGs)
- 主要用phrase structure grammer即短语语法来不断的将不同的成分嵌套在一起
- 在语义学应用非常广泛
- 主要步骤是先对每个词做词性分析part of speech, 简称POS,然后再将其组成短语,再将短语不断递归构成更大的短语
- 例如, 对于 the cuddly cat by the door,
- 先做POS分析,
- the是限定词,用Det(Determiner)表示,
- cuddly是形容词,用Adj(Adjective)代表,
- cat和door是名词,用N(Noun)表示,
- by是介词,用P(Preposition)表示
- 然后the cuddly cat构成名词短语NP(Noun Phrase),这里由Det(the)+Adj(cuddly)+N(cat)构成,by the door构成介词短语PP(Preposition Phrase), 这里由P(by)+NP(the door)构成。
- 最后,整个短语the cuddly cat by the door 是NP,由NP(the cuddly cat)+ PP(by the door)构成
- 先做POS分析,
- Dependency Parsing
- 主要展示了词语之前的依赖关系, 通常用箭头表示其依存关系, 有时也会在箭头上标出其具体的语法关系, 如是主语还是宾语关系等
- 把一句话的一个单词当做root(一般会添加一个fake ROOT), 根据单词的dependency关系来构建一个dependency tree
- 在NLP中流行
- 两种表现形式
- 一种是直接在句子上标出依存关系箭头及语法关系


- 一种是将其做成树状机构(Dependency Tree Graph)
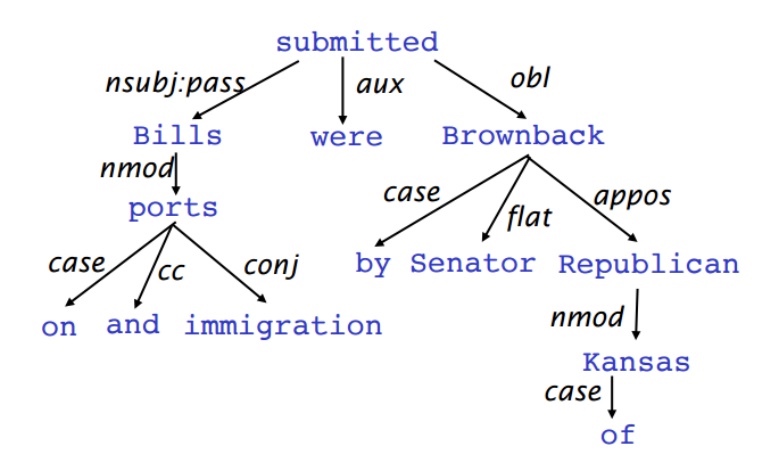
- 一种是直接在句子上标出依存关系箭头及语法关系
- Dependency Parsing可以看做是给定输入句子
$S=w_0w_1...w_n$(其中$w_0$常常是fake ROOT,使得句子中每一个词都依赖于另一个节点)构建对应的Dependency Tree Graph的任务- 而这个树的构建方法是Transition-based Dependency Parsing
Transition-based Dependency Parsing
Greedy transition-based parsing [Nivre 2003]
Transition-based Dependency Parsing可以看做是state machine, 对于 $S=w_0w_1...w_n$, state由三部分构成 $(\alpha, \beta,A)$.
$\alpha$是 S 中若干$w_i$构成的stack$\beta$是 S 中若干$w_i$构成的bufferA 是dependency arc 构成的集合,每一条边的形式是
$w_i,r,w_j$- 其中r描述了节点的依存关系如动宾关系等
初始状态时
$\alpha$仅包含ROOT$w_0$$\beta$包含了所有的单词$w_1...w_n$- A 是空集
$\varnothing$
最终的目标是
$\alpha$包含ROOT$w_0$$\beta$清空- A 包含了所有的dependency arc (A 就是想要的描述Dependency的结果)
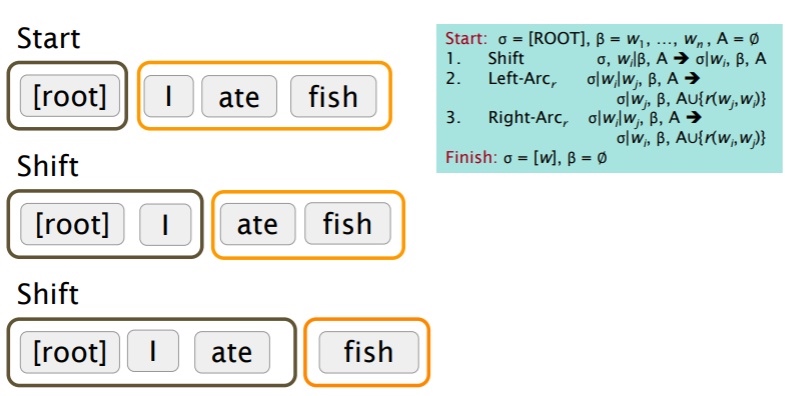
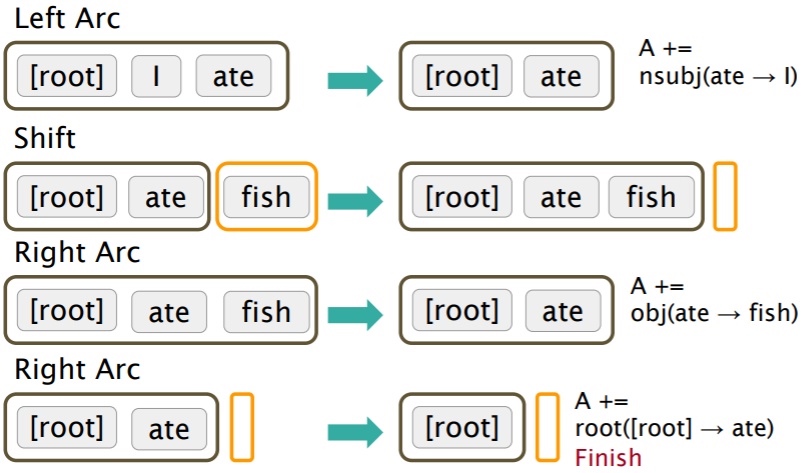
state之间的transition有三类:
- SHIFT:将buffer中的第一个词移出并放到stack上。
- LEFT-ARC: 将
$w_j,r,w_i$加入边的集合 A, 其中$w_i$是stack上的次顶层的词,$w_j$是stack上的最顶层的词 - RIGHT-ARC: 将
$w_i,r,w_j$加入边的集合 A, 其中$w_i$是stack上的次顶层的词,$w_j$是stack上的最顶层的词
不断的进行上述三类操作,直到从初始态达到最终态. 在每个状态下如何选择哪种操作呢? 当考虑到LEFT-ARC与RIGHT-ARC各有|R|(|R|为r的类的个数)种class,可以将其看做是class数为2|R|+1的分类问题,可以用SVM等传统机器学习方法解决
Evaluation
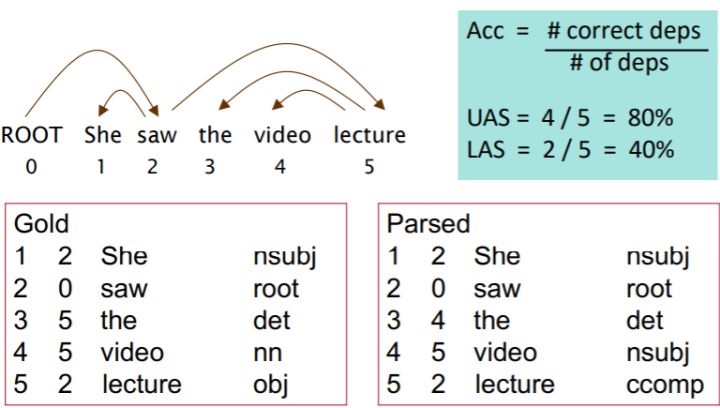
一般由两个metric
- LAS(labeled attachment score)即只有arc的箭头方向以及语法关系均正确时才算正确
- UAS(unlabeled attachment score)即只要arc的箭头方向正确即可
Neural Dependency Parsing
传统的Transition-based Dependency Parsing对feature engineering要求较高(找feature非常麻烦, 而且feature会比较sparse并且很难找到所有features, 那么用神经网络就比较intuitive), 所以可以用神经网络来减少human labor.
对于Neural Dependency Parser,其输入特征通常包含三种:
- stack和buffer中的单词及其dependent word
- 单词的Part-of-Speech tag
- 描述语法关系的arc label
输入是concat(词向量, POS向量和dependency labels向量), 其实本质上依然是一个多分类问题.

将其转换为embedding vector并将它们联结起来作为输入层,再经过若干非线性的隐藏层,最后加入softmax layer得到每个class的概率
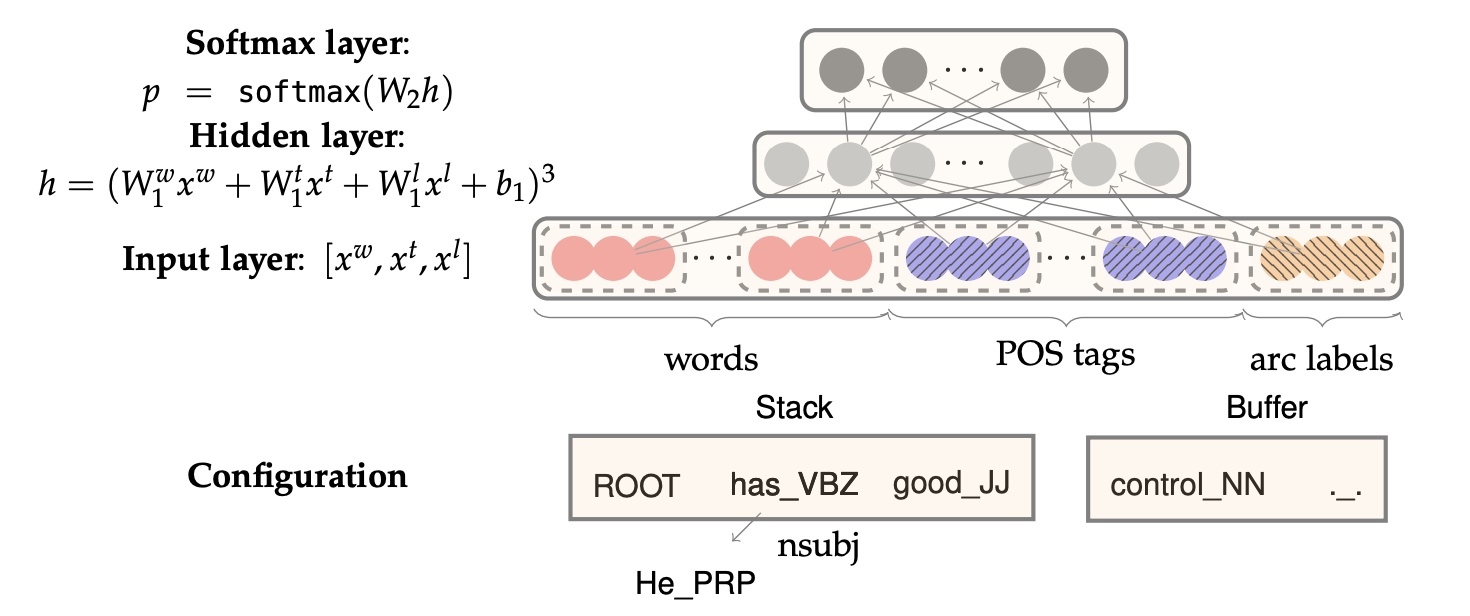
利用这样简单的前置神经网络, 就可以减少feature engineering并提高准确
RNN模型也可以应用到Dependency Parsing任务中
Lecture 06 The probability of a sentence Recurrent Neural Networks and Language Models
Language Model
- 语言建模的任务是预测下一个单词是什么
- 更正式的说法是:给定一个单词序列
$\boldsymbol{x}^{(1)}, \boldsymbol{x}^{(2)}, \ldots, \boldsymbol{x}^{(t)}$, 预测下一个单词$\boldsymbol{x}^{(t+1)}$的概率$P(\boldsymbol{x}^{(t+1)}|\boldsymbol{x}^{(t)}, \ldots, \boldsymbol{x}^{(1)})$
语言模型应用广泛,比如手机上打字可以智能预测下一个你要打的词是什么,或者谷歌搜索时自动填充问题等都属于语言模型的应用. 语言模型是很多涉及到产生文字或预测文字概率的NLP问题的组成部分,如语音识别、手写文字识别、自动纠错、机器翻译等等.
n-gram language model
- Q: 如何学习一个语言模型?
- A: 在不使用深度学习的情况下, 可以学习一个n-gram语言模型
- n-gram的定义就是连续的n个单词
- 例如对于 the students opened their __这句话,
- unigram就是”the”, “students”, “opened”, “their”,
- bigram就是”the students”, “students opened”, “opened their”,
- trigram就是” the students opened “, ” students opened their”, 以此类推
- 该模型的核心思想是n-gram的概率应正比于其出现的频率,并且假设
$P(x^{t+1})$仅仅依赖于它之前的n-1个单词,即:  通过条件概率的定义得到 $P(A|B) = \frac{P(A \cap B)}{P(B)}$
通过条件概率的定义得到 $P(A|B) = \frac{P(A \cap B)}{P(B)}$- 更具体来说,

- count是通过处理大量文本对相应的n-gram出现次数计数得到的
n-gram模型主要有两大问题:
- 稀疏问题 Sparsity Problem.
- 有些sequence of words从来没在数据集中出现过, 那么这种词序列出现的概率为0 (即分子或分母为0), 解决办法:
- smoothing, 比如Laplace smoothing默认就会给每种情况一个较小的概率.
- backoff, 也就是把单词所condition的词序列长度减小, 那么这个序列就更可能出现了 (use bigram instead of trigram)
- 并且随着n的增大,稀疏性更严重
- 有些sequence of words从来没在数据集中出现过, 那么这种词序列出现的概率为0 (即分子或分母为0), 解决办法:
- 必须存储所有的n-gram对应的计数,随着n的增大,模型存储量也会增大, 所以一般n都小于5
这些限制了n的大小,但如果n过小,则无法体现稍微远一些的词语对当前词语的影响,这会极大的限制处理语言问题中很多需要依赖相对长程的上文来推测当前单词的任务的能力
n-gram Language Models can be used to generate text.
Fixed-window neural Language Model
一个自然的将神经网络应用到语言模型中的思路是window-based DNN,即将定长窗口中的word embedding连在一起,将其经过神经网络做对下一个单词的分类预测,其类的个数为语库中的词汇量,如下图所示
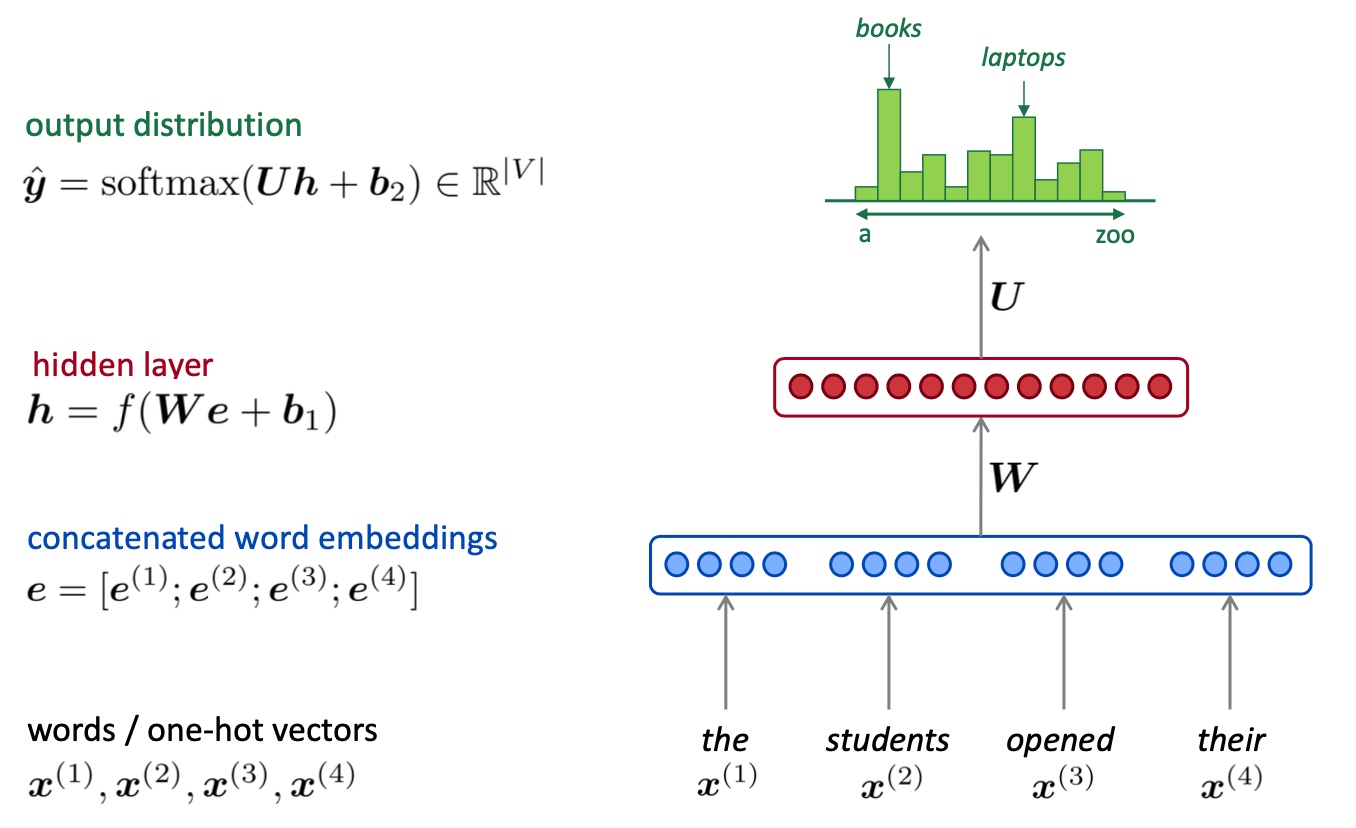
- Pros:
- 解决了稀疏问题
- 解决了存储问题 (不需要储存所有观察到的n-grams)
- Cons:
- 窗口大小固定
- 扩大窗口会使矩阵W变大 (窗口再大也不够用)
$x_1, x_2$乘以完全不同的权重, 没有任何可共享的参数
RNN
RNN(Recurrent Neural Network)结构通过不断的应用同一个矩阵W可实现参数的有效共享,并且没有固定窗口的限制. 其基本结构如下图所示:
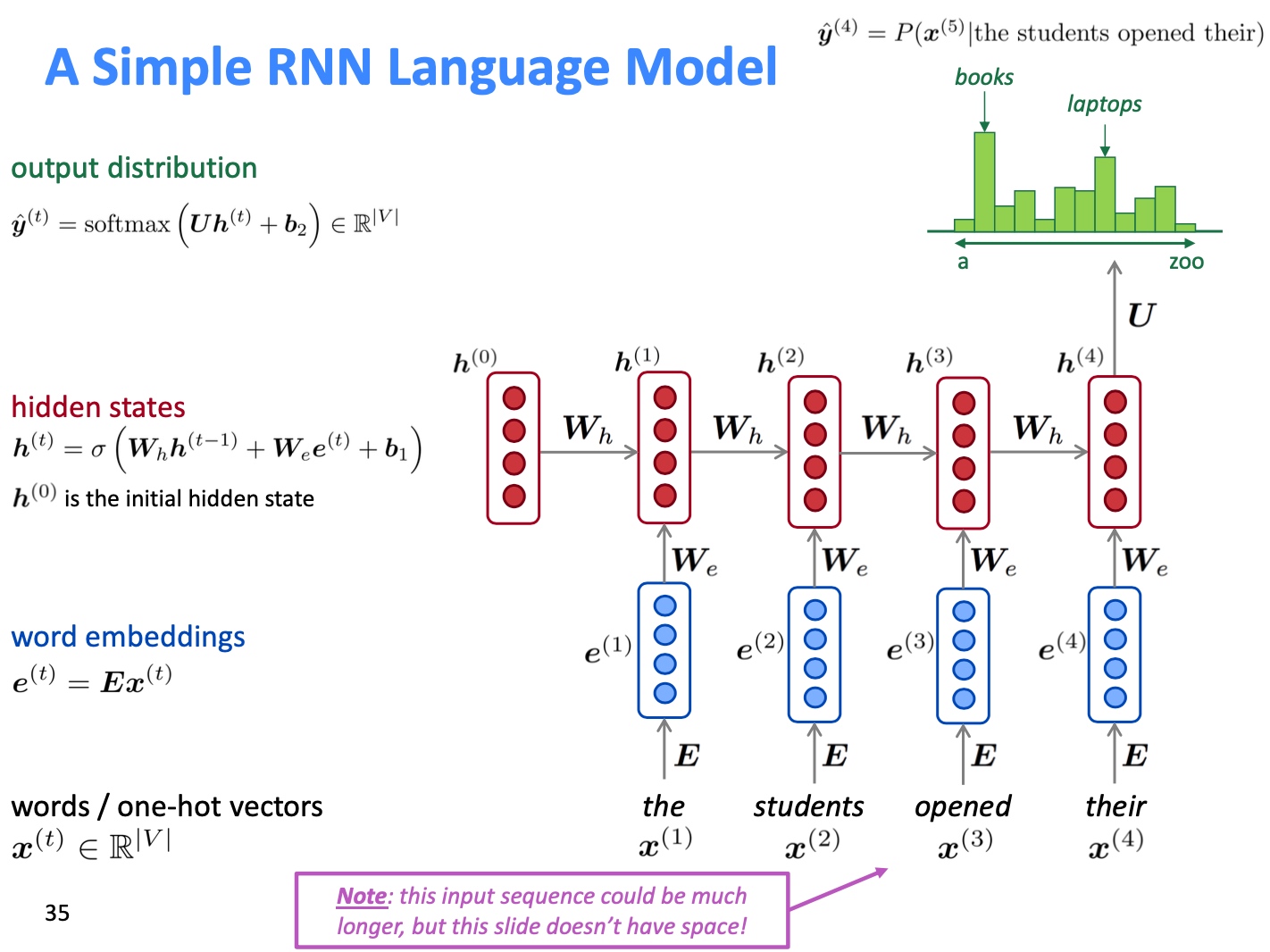
- Pros
- 可以处理任意长度的输入
- 步骤 t 的计算(理论上)可以使用许多步骤前信息
- 模型大小不会随着输入的增加而增加
- 在每个时间步上应用相同的权重矩阵,因此在处理输入时具有 对称性 (有效的进行了参数共享)
- Cons
- 递归(下个input是上个的output)计算速度慢 (由于需要顺序计算而不是并行计算, RNN计算较慢)
- 在实践中,很难从许多步骤前返回信息 (由于梯度消失等问题距离较远的早期历史信息难以捕捉)
Training a RNN Language Model
RNN的训练过程同样依赖于大量的文本,在每个时刻t计算模型预测的输出 $\hat{\boldsymbol{y}}^{(t)}$ 与真实值 $\boldsymbol{y}^{(t)}$ 即 $x^{(t+1)}$ 的cross-entropy loss,即
$$J^{(t)}(\theta)=C E\left(\boldsymbol{y}^{(t)}, \hat{\boldsymbol{y}}^{(t)}\right)=-\sum_{w \in V} \boldsymbol{y}_{w}^{(t)} \log \hat{\boldsymbol{y}}_{w}^{(t)}=-\log \hat{\boldsymbol{y}}_{\boldsymbol{x}_{t+1}}^{(t)}$$
对于文本量为T的总的损失即为所有交叉熵损失的平均值:
$$J(\theta)=\frac{1}{T} \sum_{t=1}^{T} J^{(t)}(\theta)=\frac{1}{T} \sum_{t=1}^{T}-\log \hat{\boldsymbol{y}}_{\boldsymbol{x}_{t+1}}^{(t)}$$
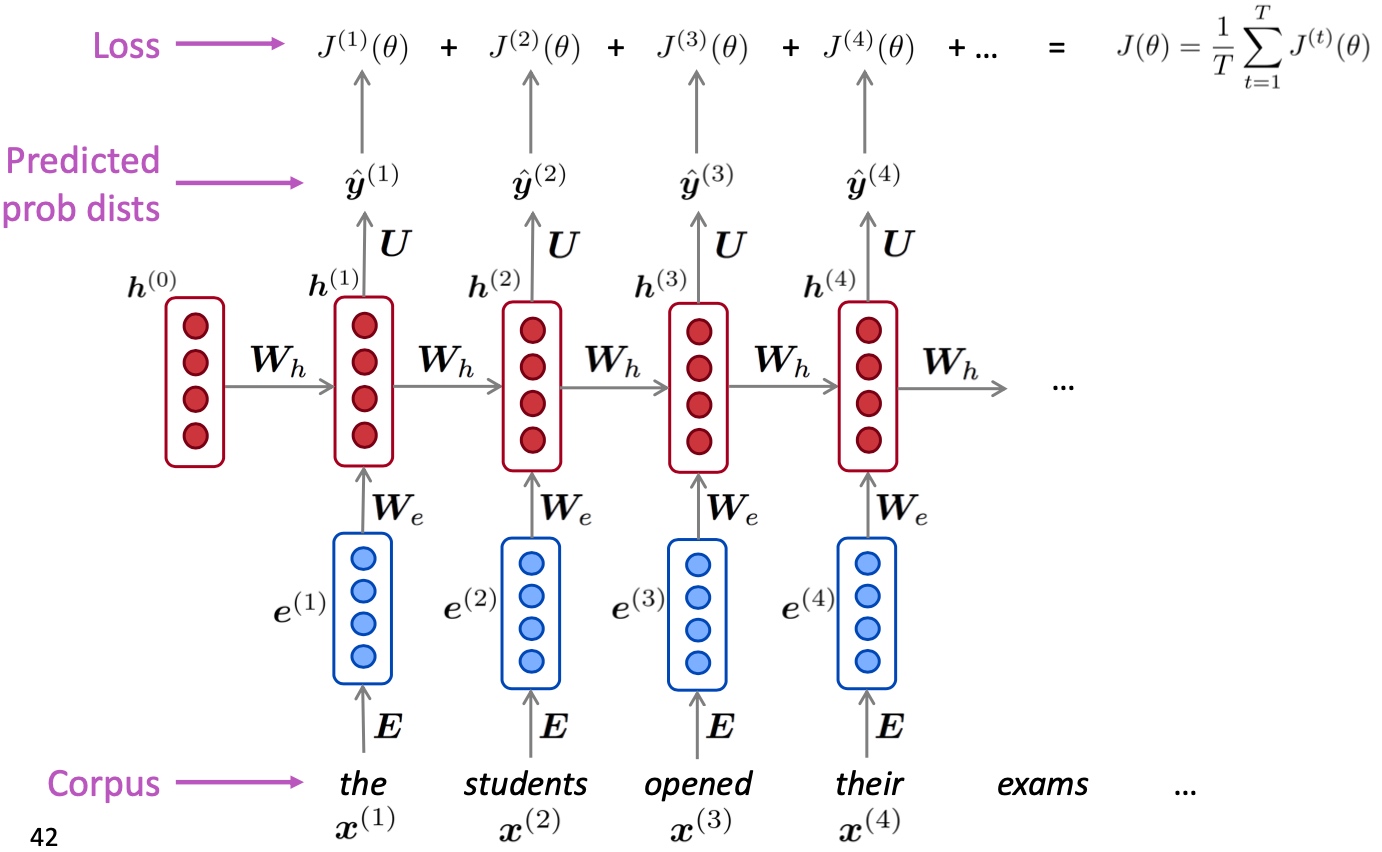
- 上述例子中, 一个x输入就是一个单词, 这样计算整个语料库(x^1..x^T)的损失和梯度就太过昂贵了; 在实践中, 一个x输入通过是一个句子或是文档.
- 计算一个句子的损失 J(θ) (实际上是一批句子),计算梯度和更新权重.
Backpropagation for RNNs
Multivariable Chain Rule:
对于一个多变量函数 f(x,y) 和两个单变量函数 x(t) 和 y(t) ,其链式法则如下:
$$\frac{d}{d t} f(x(t), y(t))=\frac{\partial f}{\partial x} \frac{d x}{d t}+\frac{\partial f}{\partial y} \frac{d y}{d t}$$
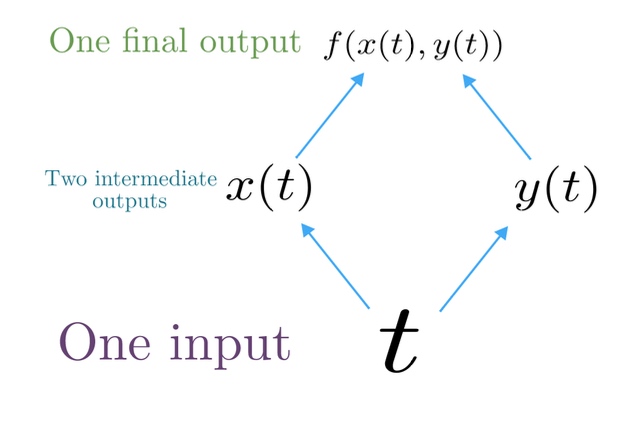
在RNN中:
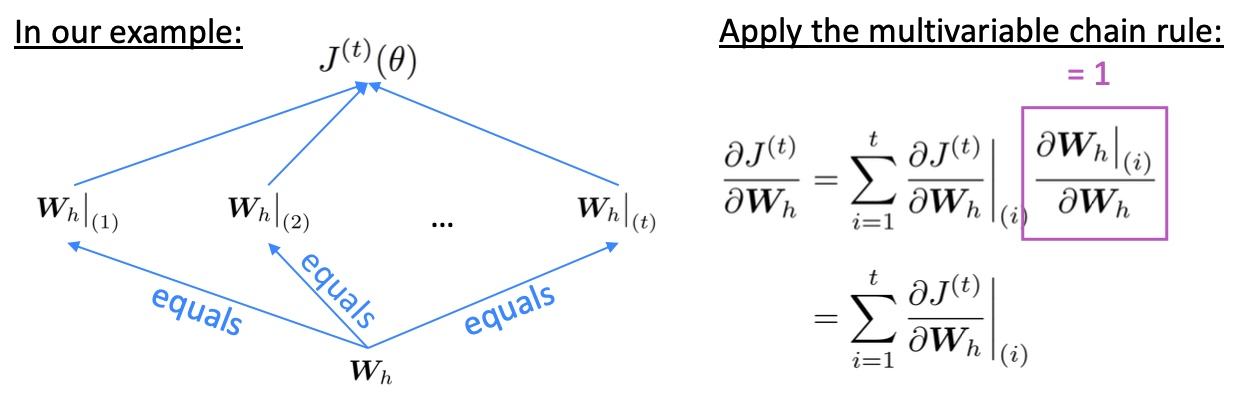
Backpropagation for RNNs:
- Q: 所以这个参数共享(可重复)的权重矩阵
$W_h$的偏导数怎么求? - A: 重复权重的梯度就是在每个时间步的梯度的总和
$\frac{\partial J^{(t)}}{\partial \boldsymbol{W}_{\boldsymbol{h}}}=\sum_{i=1}^{t}\left.\frac{\partial J^{(t)}}{\partial \boldsymbol{W}_{\boldsymbol{h}}}\right|_{(i)}$
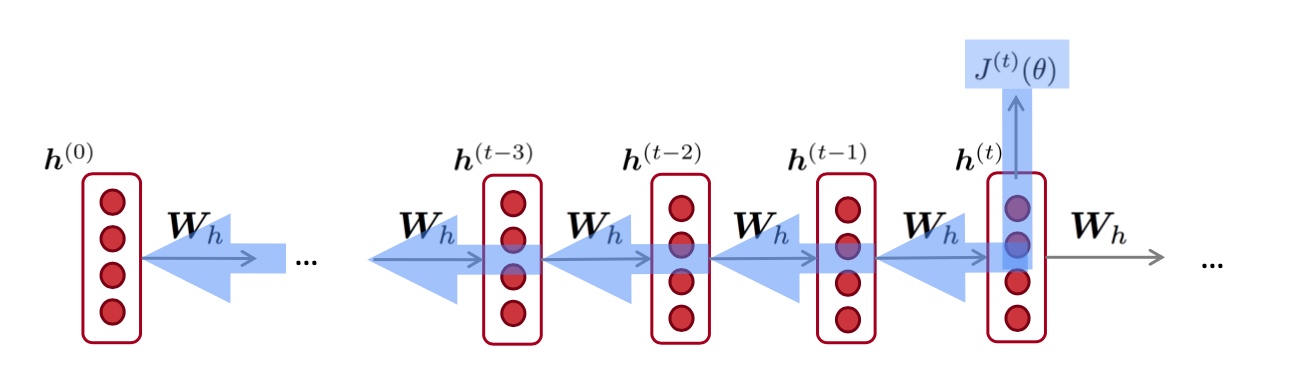
- Q: 如何计算
$\sum_{i=1}^{t}\left.\frac{\partial J^{(t)}}{\partial \boldsymbol{W}_{\boldsymbol{h}}}\right|_{(i)}$? - A: 根据时间步长 i=t,…,0 反向传播. 累加梯度. 这个算法叫做”backpropagation through time”
Evaluating Language Models
语言模型的评估指标是perplexity,即文本库的概率的倒数,也可以表示为损失函数的指数形式,所以perplexity越小表示的语言模型越好.

$$=\prod_{t=1}^{T}\left(\frac{1}{\hat{y}_{x_{t+1}}^{(t)}}\right)^{1 / T}=\exp \left(\frac{1}{T} \sum_{t=1}^{T}-\log \hat{\boldsymbol{y}}_{\boldsymbol{x}_{t+1}}^{(t)}\right)=\exp (J(\theta))$$
等于交叉熵损失 J(θ) 的指数