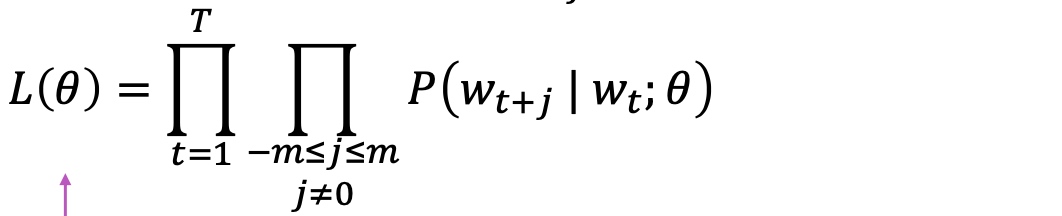Meaning of words

• Denotational semantics (signifier(symbol) <=> signified(idea or thing)):
  • Localist representation (regard words as discrete symbols: hotel, motel)
  • One-hot Vector
    • vector dimension might be too big
    • there is no natural notion of similarity
• Distributional semantics (A word’s meaning is given by the words that frequently appear close-by (context›)):
  • Context E.g.
  • Word Vector (Word Emdeddings) E.g.
  • words with similar context are grouped closely

SVD Based Method

Use SVD to find word vector

• loop over a massive dataset and accumulate word co-occurrence counts in some form of a matrix X
  • Word-Word Co-occurrence Matrix:
• perform Singular Value Decomposition(SVD) on X to get a $USV^T$ decomposition
• use the rows of U as the word embeddings for all words in our dictionary
  

Iteration Based Method - Word2vec

• Language Models (Unigrams, Bigrams, etc.) - a model that will assign a probability to a sequence of tokens
  • A good language model will give valid sentence(syntactically and semantically) a high probability. $P(w_1,w_2,…,wn)=\prod^n{i=1}P(w_i)$ (Unigrams)
  • Bigrams - the probability of the sequence depend on the pairwise probability of a word in the sequence and the word next to it. $P(w_1,w_2,…,wn)=\prod^n{i=2}P(wi|w{i-1})$
• w2v(Mikolov et al. 2013) is a framework for learning word vectors
• Idea:
  • A large corpus of text
  • Every word in a fixed vocabulary is represented by a vector
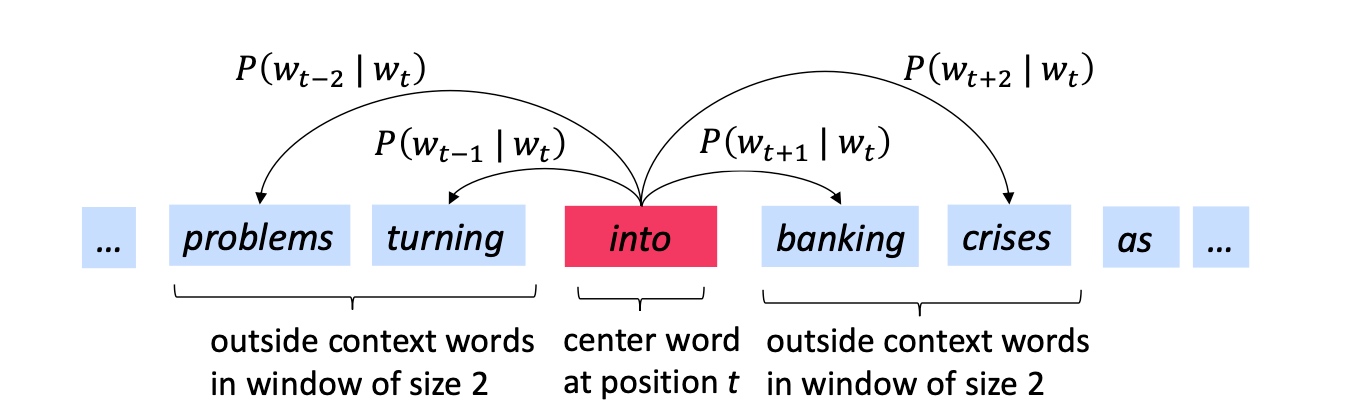
  • Go through each position t in the text, which has a center word c and context (“outside”) words o
  • Use the similarity of the word vectors for c and o to calculate the probability of o given c (or vice versa)
  • Keep adjusting the word vectors to maximize this probability
• Detail:
  • Windows and process for computing $P(w_{t+j}|w_t)$
    1. Randomly initialize all word vectors
    2. Iterate through each word in the text/corpus
       • given a center word c, maximize the probability of outside context words 0
    3. 
• Objective function(loss/cost function)
  • Likelihood:
    • 
  • Convert (average) negative log likelihood into objective function ($J(\theta)$)
    • 
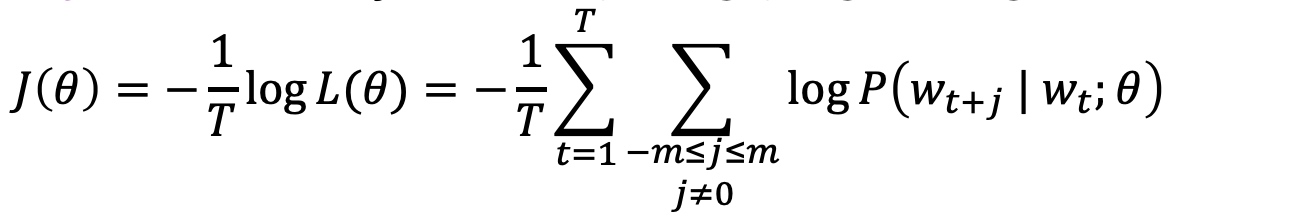
    • minus sign, turn maximization into minimization
    • 1/T, for keeping scale
    • log function, turn the product into sum
  • The way to calculate $P(w_{t+j}|w_t)$
    • Use 2 vectors per word
      • $v_w, u_w$ when w is a center word or context word respectively
      • E.g. $P(u{problems}|v{into})$
  • 
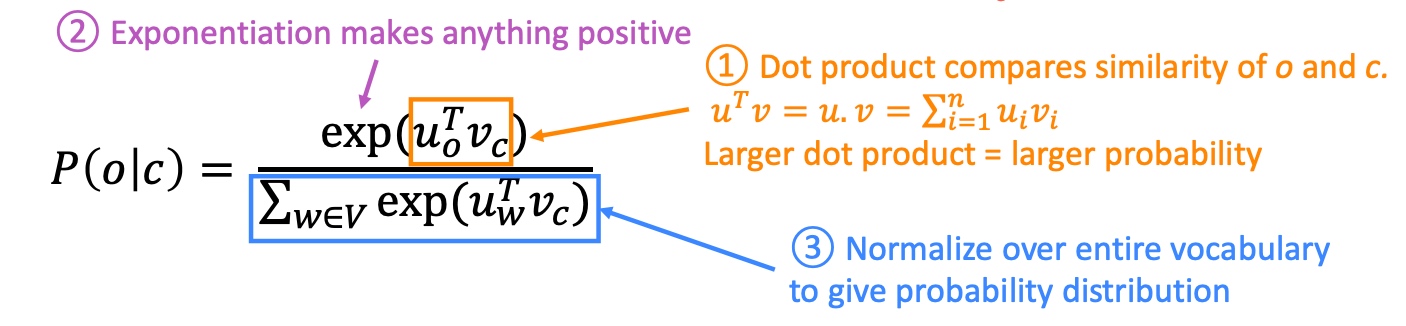
  • Extra notes: Softmax function (map any numbers into a probability distribution)
    • 
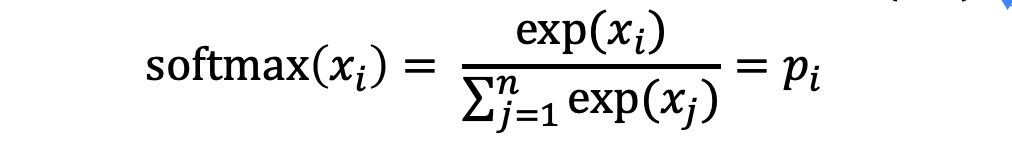
    • MAX part: exp function makes big numbers way bigger (amplifies largest $x_i$)
    • SOFT part: it spreads a little bit of probability mass everywhere else (still assigns some probability to smaller $x_i$)
• Optimization
• Model
  • Skip-grams(SG)
    • Got 1 center word, and predict all the words in context
    • generate our one-hot input vector $x \in R^{|V|}$ of the center word
    • get embedded word vector for the center word $v_c = V_x \in R^n$
    • generate a score vector $z = U v_c$
    • turn the score vector into probabilities, $yˆ = softmax(z)$. Note that $yˆ{c-m} ,…,yˆ{c-1} ,yˆ{c+1} ,…,yˆ{c+m}$ are the probabilities of observing each context word.
    • We desire probability vector generated to match the true prob- abilities which is $y^{(c−m)}, …, y^{(c−1)}, y^{(c+1)}, …, y^{(c+m)}$, the one hot vectors of the actual output.
  • Continuous Bag of Words (CBOW)
    • Got all of the outside words, and predict the center word
  • SG better than CBOW
    • In CBOW the vectors from the context words are averaged before predicting the center word. In skip-gram there is no averaging of embedding vectors. It seems like the model can learn better representations for the rare words when their vectors are not averaged with the other context words in the process of making the predictions.
    • E.g. In CBOW, today is [] day, [] would probably be beautiful or nice, it is designed to predict the most probable words, it won’t consider the word like delightful; SG is designed to predict the context, Given the word delightful, it might tell the context is today is [] day or some other relevant context.
• Training Methods
  • Negative sampling
  • Hierarchical softmax