Transformer

3 minutes read
Model
#Model
views 633 words

1. 背景

自从Attention机制在提出之后，加入Attention的Seq2Seq模型在各个任务上都有了提升，所以现在的seq2seq模型指的都是结合RNN和attention的模型. 传统的基于RNN的Seq2Seq模型难以处理长序列的句子，无法实现并行，并且面临对齐的问题.

所以之后这类模型的发展大多数从三个方面入手：

  • input的方向性：单向 -> 双向
  • 深度：单层 -> 多层
  • 类型：RNN -> LSTM / GRU

但是依旧收到一些潜在问题的制约，神经网络需要能够将源语句的所有必要信息压缩成固定长度的向量. 这可能使得神经网络难以应付长时间的句子，特别是那些比训练语料库中的句子更长的句子；每个时间步的输出需要依赖于前面时间步的输出，这使得模型没有办法并行，效率低；仍然面临对齐问题.

再然后CNN由计算机视觉也被引入到deep NLP中，CNN不能直接用于处理变长的序列样本但可以实现并行计算. 完全基于CNN的Seq2Seq模型虽然可以并行实现，但非常占内存，很多的trick，大数据量上参数调整并不容易.

Transformer的创新点在于抛弃了之前传统的encoder-decoder模型必须结合CNN或者RNN的固有模式，只用Attention. 其主要目的在于减少计算量和提高并行效率的同时不损害最终的实验结果.

2. 整体框架

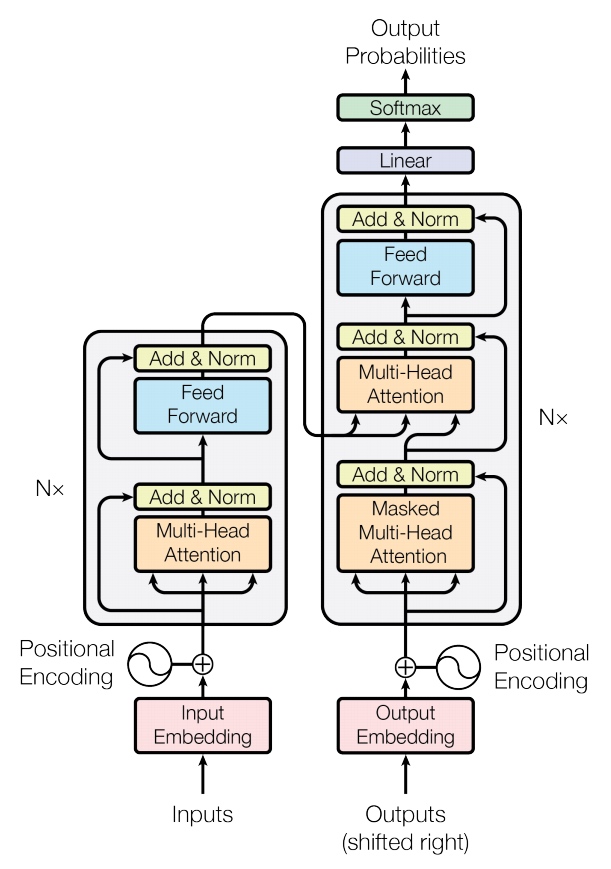
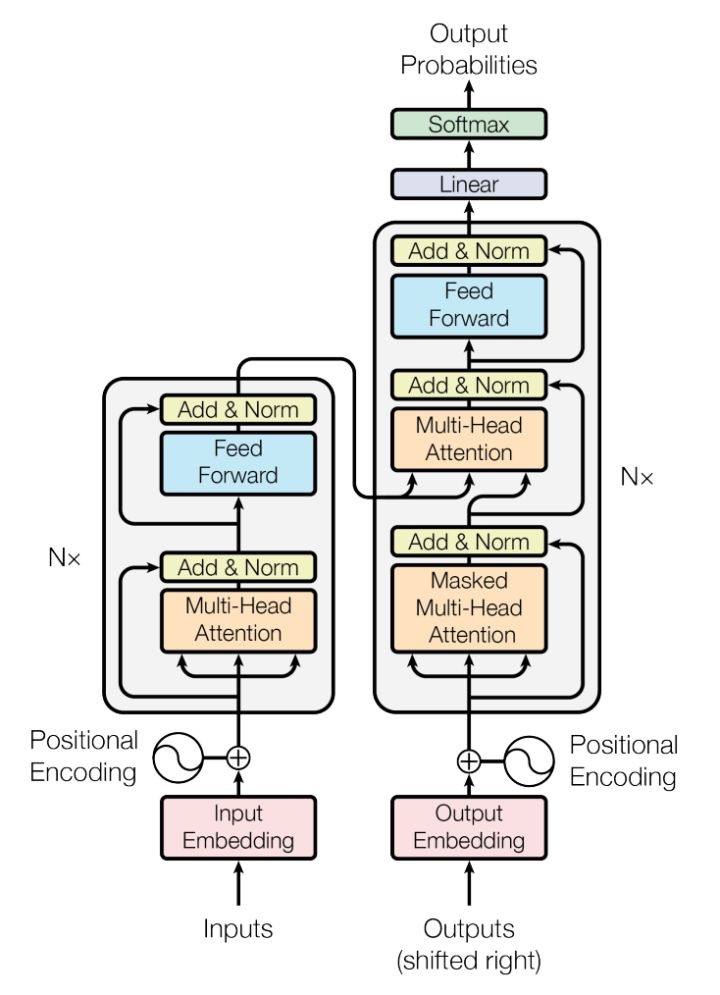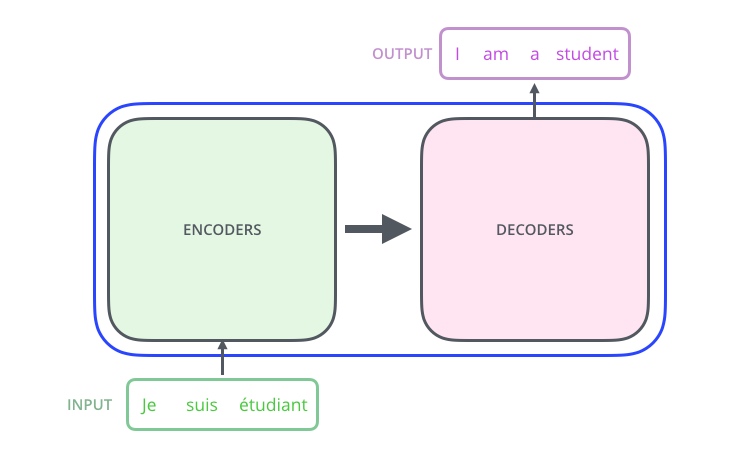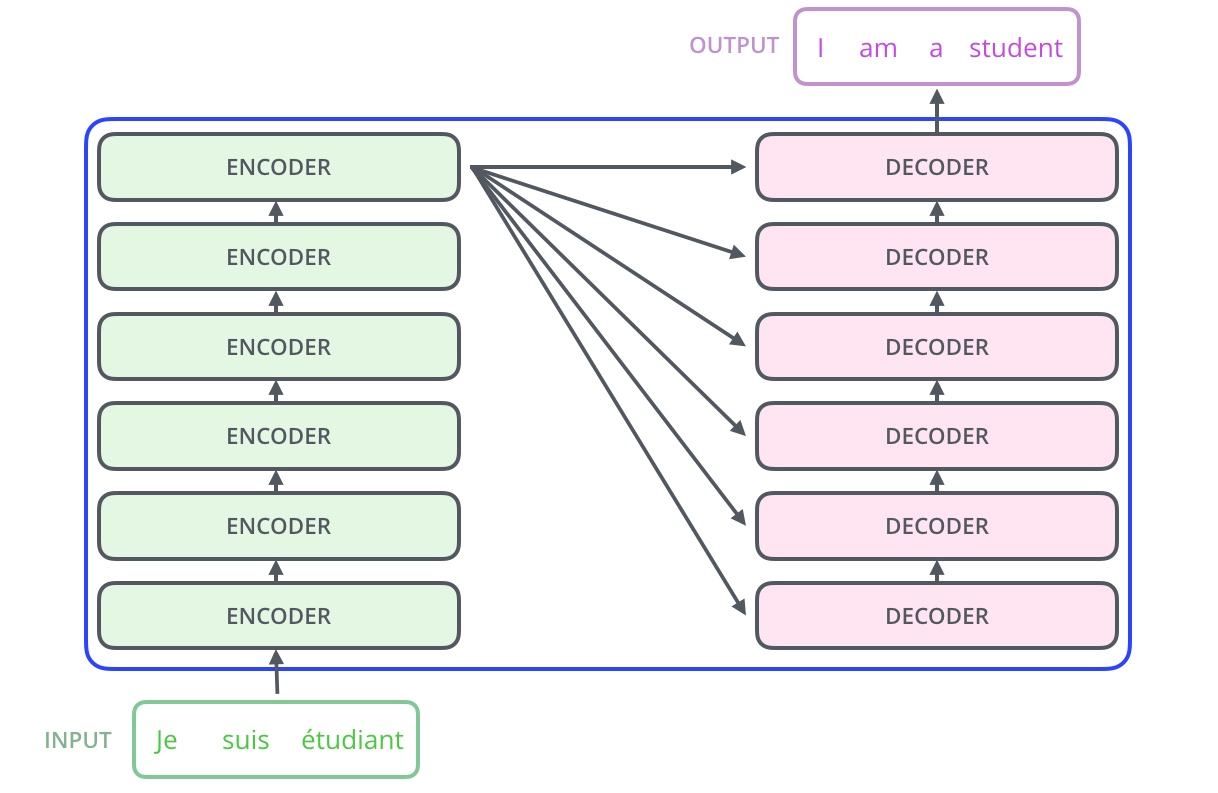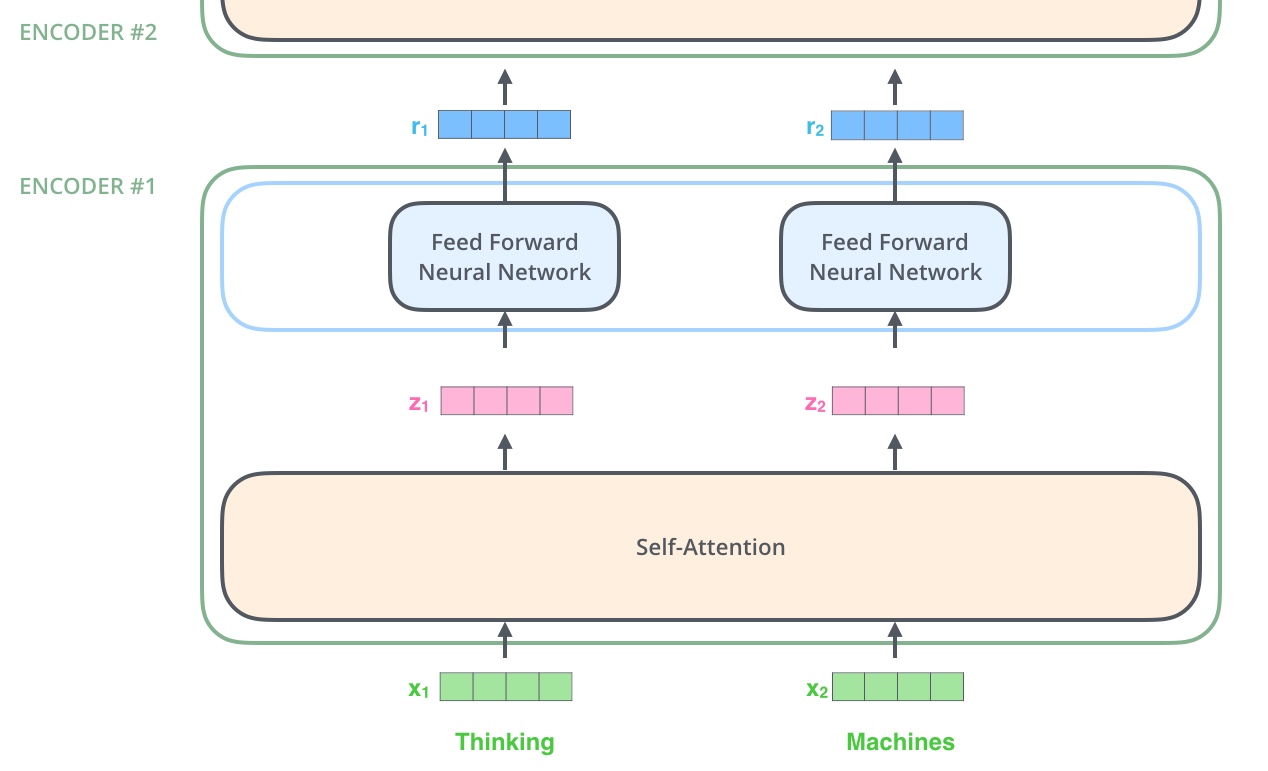
其实这就是一个Seq2Seq模型，左边一个encoder把输入读进去，右边一个decoder得到输出： 左边的encoders和右边的decoders都是由6层组成，内部左边encoder的输出和右边decoder结合的直观图如下: 每一个encoder和decoder的内部简版结构如下图 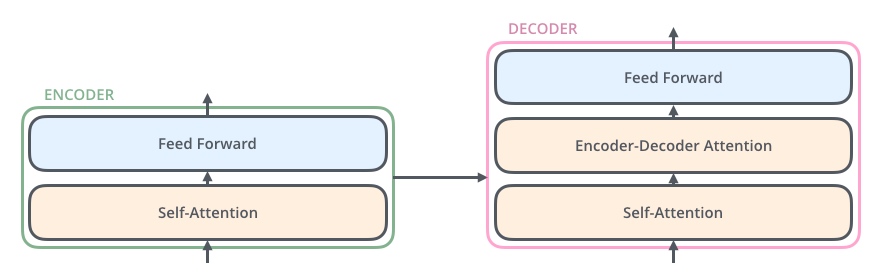对于encoder，包含两层，一个self-attention层和一个前馈神经网络，self-attention能帮助当前节点不仅仅只关注当前的词，从而能获取到上下文的语义.

decoder也包含encoder提到的两层网络，但是在这两层中间还有一层attention层，帮助当前节点获取到当前需要关注的重点内容.

3. Encoder层

首先，模型需要对输入的数据进行一个embedding操作，通过Word2Vec等词嵌入方法将输入语料转化成特征向量 (论文中使用的词嵌入的维度为$d_{model}=512$). -w316

然后输入到encoder层, self-attention处理完数据后把数据送给前馈神经网络，前馈神经网络的计算可以并行，得到的输出会输入到下一个encoder.

Self-Attention

其思想和attention类似，但是self-attention是Transformer用来将其他相关单词的’理解’转换成正在处理的单词的一种思路，看个例子： The animal didn't cross the street because it was too tired 这里的it到底代表的是animal还是street呢? 对于人来说能很简单的判断出来，但是对于机器来说，是很难判断的，self-attention就能够让机器把it和animal联系起来.

1、首先，self-attention会从每个编码器的输入向量 (每个单词的词向量)计算出三个新的向量，在论文中，向量的维度是512维，把这三个向量分别称为Query、Key、Value(查询向量,键向量,值向量). 这三个向量是通过词嵌入与三个权重矩阵后相乘创建的, 这三个权重矩阵都是随机初始化的(通过BP去更新)，维度都为(512,64), 其值在BP的过程中会一直进行更新, 最终得到的这三个向量的维度是64 ($d_k=d_v=d_q=\frac{d_{model}}{h} = 64$, h=8表示8次Attention操作, 多头注意力后面会讲到). 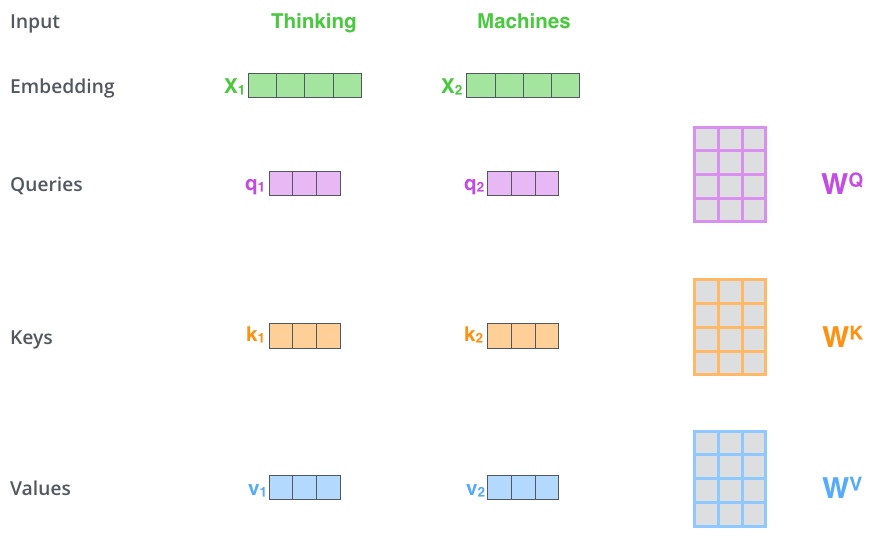($X_1$与$W_Q$权重矩阵相乘得到$q_1$, 就是与这个单词相关的查询向量. 最终使得输入序列的每个单词的创建一个查询向量、一个键向量和一个值向量)

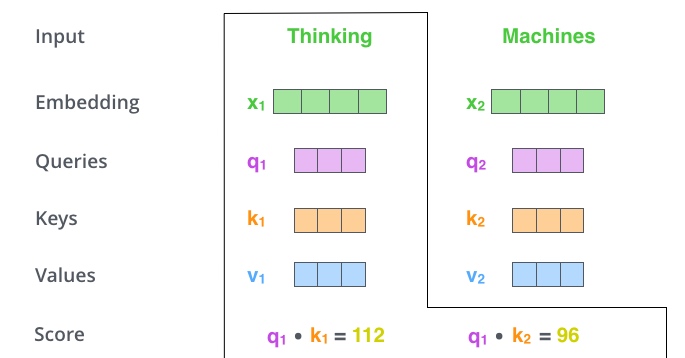
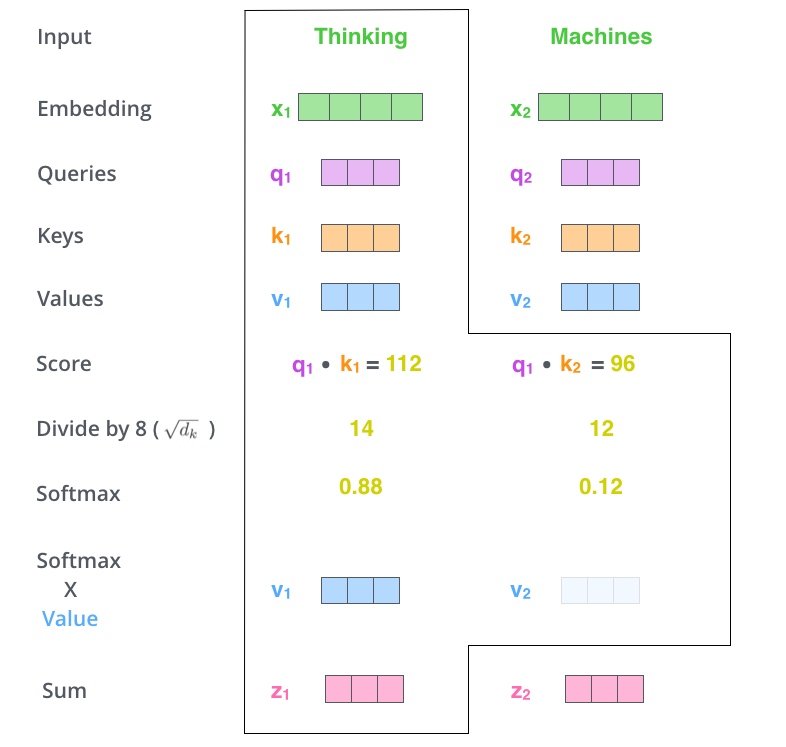
2、计算self-attention的分数值，该分数值决定了当在某个位置encode一个词时，对输入句子的其他部分的关注程度. 这个分数值的计算方法是Query与Key做点乘. 以下图为例, 首先需要针对’Thinking’这个词, 计算出其他词对于该词的一个分数值，首先是针对于自己本身的分数即$q_1·k_1$, 然后是针对于第二个词的分数即$q_1·k_2$

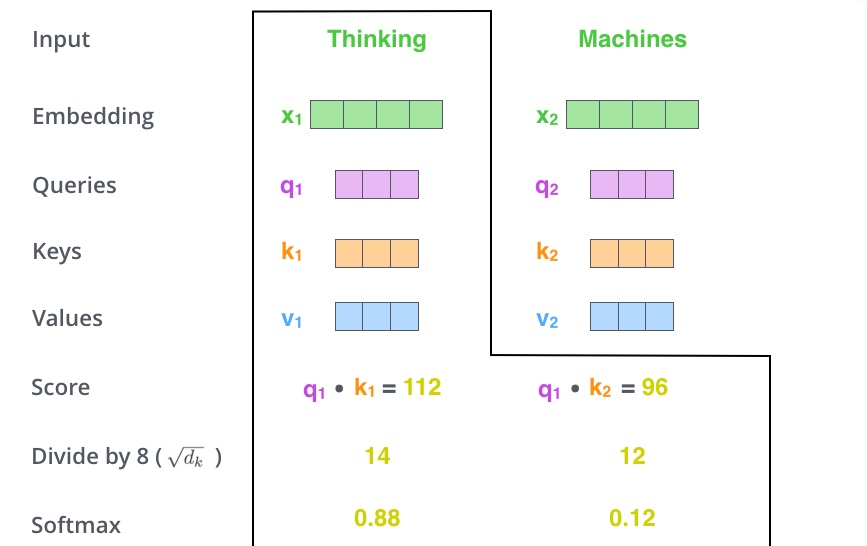
3、接下来，把点成的结果除以一个常数，这里除以8 (8是论文中使用的键向量的维数64的平方根，这会让梯度更稳定. 这里也可以使用其它值，8只是默认值). 然后把得到的结果做一个softmax的计算, softmax的作用是使所有单词的分数归一化, 得到的分数都是正值且和为1. 得到的结果即是每个词对于当前位置的词的相关性大小(这个softmax分数决定了每个单词对编码当下位置（’Thinking’）的贡献), 当然，当前位置的词相关性肯定会会很大.

4、下一步就是把Value(值向量)和softmax得到的值进行相乘, 并相加 (自注意力的另一种解释就是在编码某个单词时，就是将所有单词的表示（值向量）进行加权求和，而权重是通过该词的表示（键向量）与被编码词表示（查询向量）的点积并通过softmax得到). 得到的结果即是self-attetion在该位置的输出

在实际的应用场景，为了提高计算速度，采用的是矩阵运算的方式, 直接计算出Query, Key, Value的矩阵. 为此，将将输入句子的词嵌入装进矩阵X中, 将其乘以训练的权重矩阵($W^Q，W^K，W^V$) 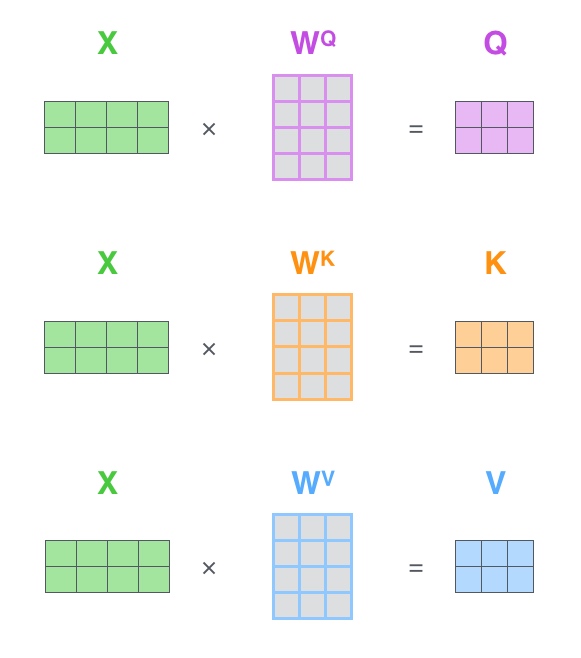(X矩阵中的每一行对应于输入句子中的一个单词. 可以看到词嵌入向量 (512, 或图中的4个格子)和Q/K/V向量(64, 或图中的3个格子)的大小差异)

把得到的新矩阵Q与K相乘，除以一个常数，做softmax操作，最后乘上V矩阵 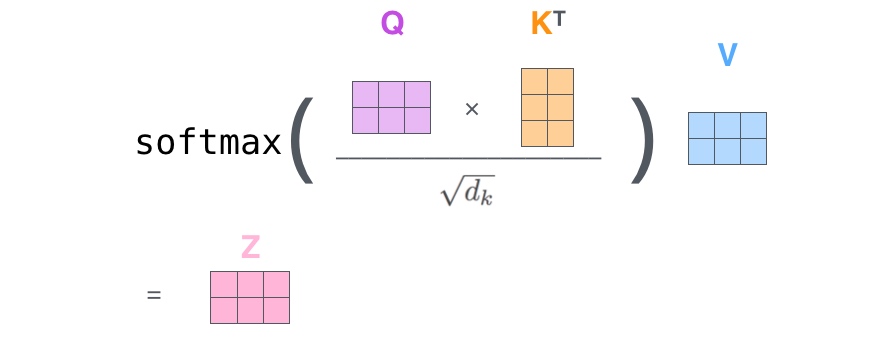这种通过 query 和 key 的相似性程度来确定 value 的权重分布的方法被称为scaled dot-product attention:

$A(Q,K,V) = softmax(\frac{QK^T}{\sqrt{d_k}})V$

这个公式是论文的关键. Q和K是每个单词在64维空间中的不同投影. 因此，可以考虑这些投影的点积作为标记投影之间相似性的度量. 对于通过Q投射的每个矢量，与通过K投影的矢量进行点积，其结果可以表示这些矢量之间的相似性. 如果令$v_i$为第i个单词通过Q得到的投影，$v_j$为第j个单词通过K得到的投影，则它们的点积可以看作：

$v_iv_j = cos(v_i,v_j) ||v_i||_2||v_j||_2$

因此，这是对$v_i, v_j$的方向有多相似以及它们的长度有多大的度量（方向越接近，长度越大，点积越大）.

Multi-Headed Attention

通过增加一种叫做“多头”注意力（’multi-headed’ attention）的机制，论文进一步完善了自注意力层, 它主要扩展了模型专注于不同位置的能力. 在上面的例子中, 虽然每个编码都在$z_1$中有或多或少的体现, 但是它可能被实际的单词本身所支配. 如果翻译一个句子, 比如The animal didn’t cross the street because it was too tired, 我们会想知道’it’指的是哪个词, 这时模型的’多头’注意机制会起到作用.

它给出了注意力层的多个’表示子空间’(representation subspaces). 对于’多头’注意机制, 可以有多个查询/键/值权重矩阵集(Transformer使用八个注意力头, 因此对于每个编码器/解码器有八个矩阵集合). (Multi-Head Attention就是把Scaled Dot-Product Attention的过程做8次, 即不仅仅只初始化一组Q、K、V的矩阵，而是初始化多组, 最后得到的结果是8个矩阵)

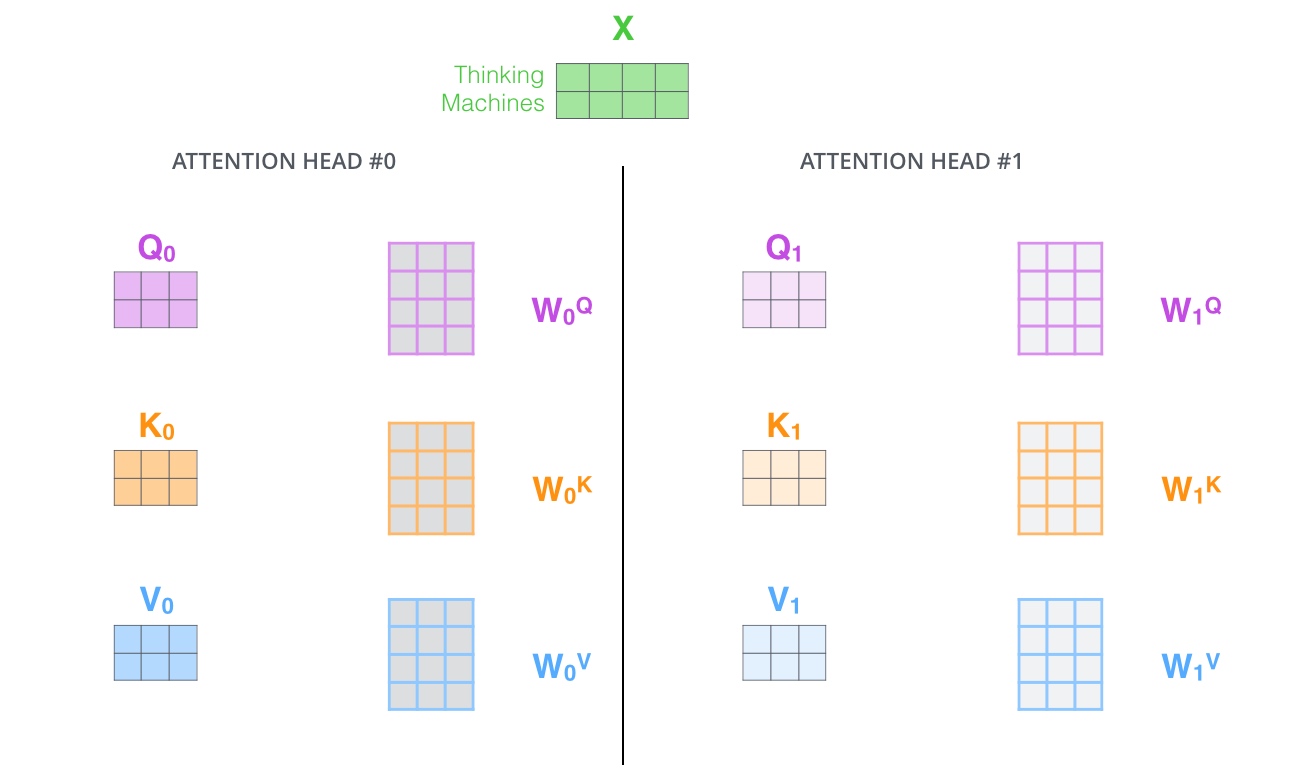(在’多头’注意机制下, 为每个头保持独立的查询/键/值权重矩阵, 从而产生不同的查询/键/值矩阵. 和之前一样, 拿X乘以$W^Q/W^K/W^V$矩阵来产生查询/键/值矩阵)

只需八次不同的权重矩阵运算, 就会得到八个不同的Z矩阵 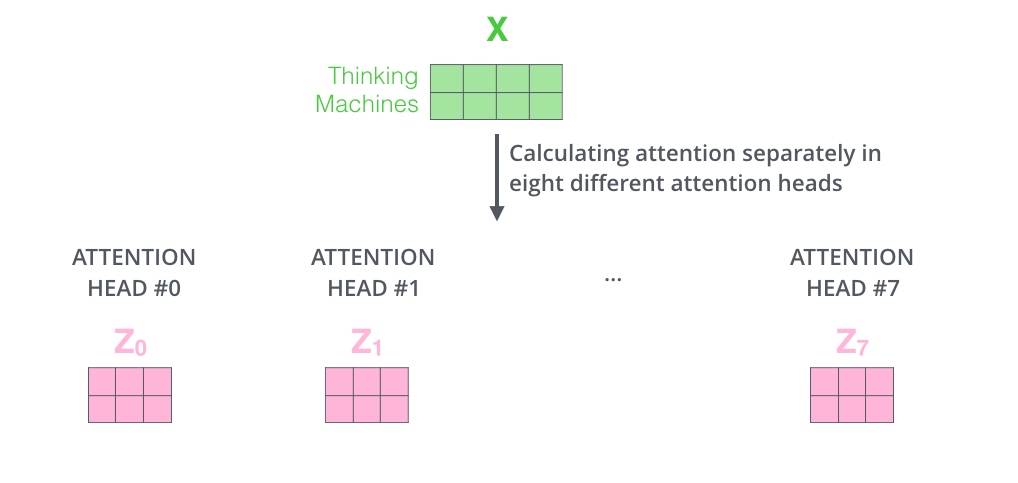但是前馈神经网络没法输入八个矩阵, 所以需要一种方式，把八个矩阵压缩为一个.

  1. 把8个矩阵连在一起，这样会得到一个大的矩阵
  2. 再随机初始化一个权重矩阵$W^O$和这个组合好的矩阵相乘, 最后得到一个最终的矩阵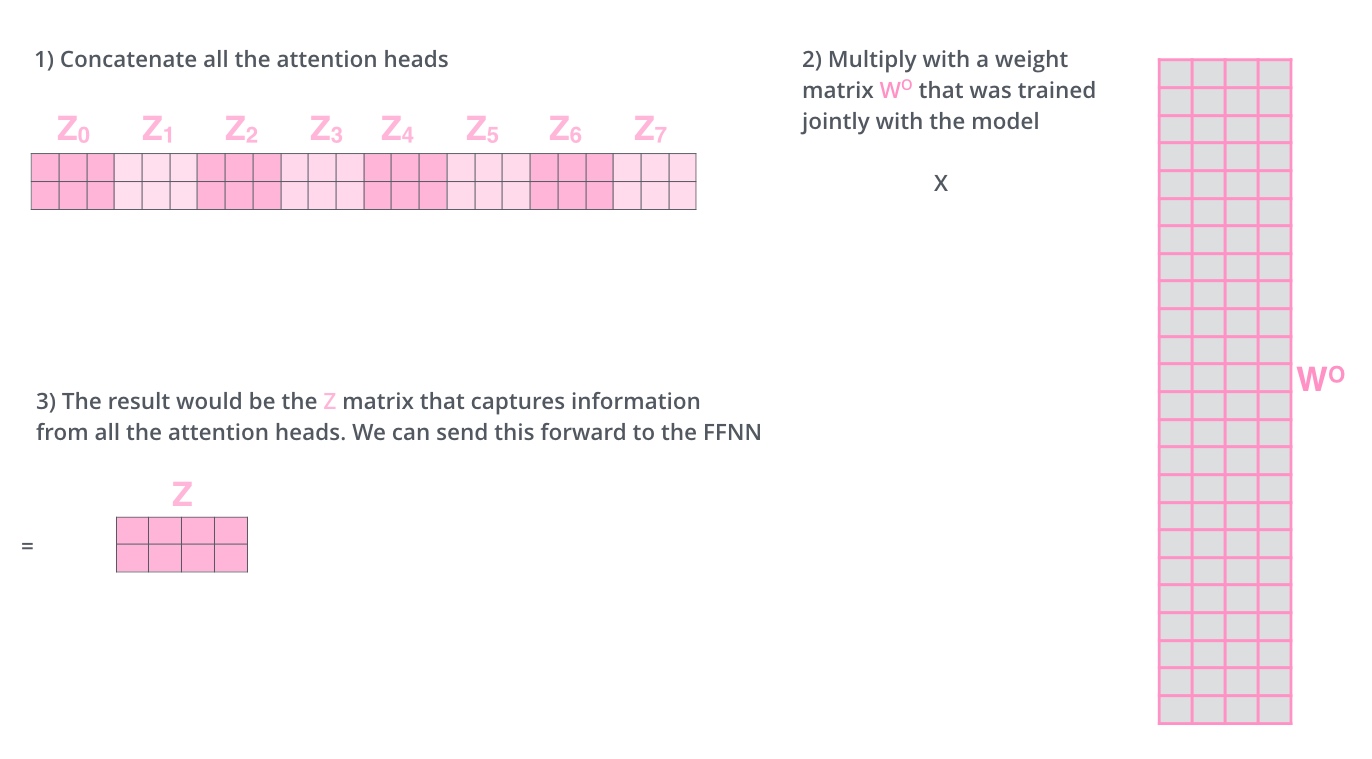

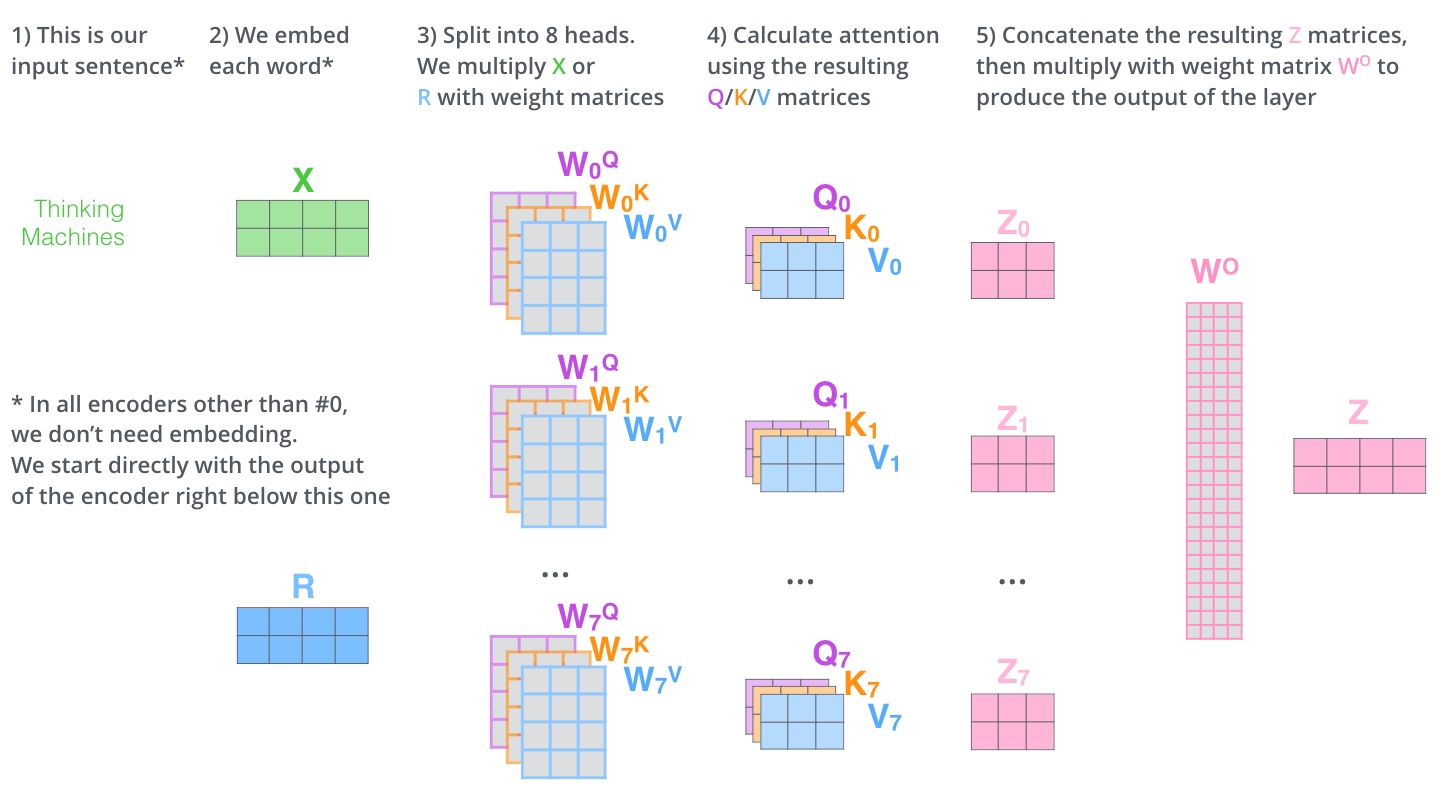
multi-headed attention的总体流程:

在例句中编码’it’一词时，不同的注意力’头’集中在哪里：

(其中, 一个注意力头集中在“animal”上(橙色列)，而另一个则集中在“tired”上(绿色列)，从某种意义上说，模型对“it”一词的表达在某种程度上是“animal”和“tired”的代表)

如果把所有的attention都加到图示里，事情就更难解释了：

Position-wise Feed-forward Networks

在进行了Attention操作之后，encoder和decoder中的每一层都包含了一个全连接前向网络，对每个position的向量分别进行相同的操作，包括两个线性变换和一个ReLU激活输出:

公式:

$FFN(x) = max(0, xW_1+b_1)W_2 +b_2$

其中每一层的参数都不同

Positional Encoding

使用位置编码表示序列的顺序. 因为transformer完全没用到RNN, 所以需要自己处理. 原论文中使用了固定的static embedding(如下,代码可参考link), 而不是通过学习的. 但是BERT用的是positional embeddings, 只需将token的position传到embedding layer即可.

到目前为止，transformer模型中还缺少一种解释输入序列中单词顺序的方法. 为了处理这个问题，transformer给encoder层和decoder层的输入添加了一个额外的向量Positional Encoding, 维度和词嵌入的维度一样，这个向量采用了一种很独特的方法来让模型学习到这个值，这个向量能决定当前词的位置，或者说在一个句子中不同的词之间的距离. 这个位置向量的具体计算方法有很多种，论文中的计算方法如下

$PE(pos,2i)=sin(\frac{pos}{10000 \frac{2i}{d_{model}}})$

$PE(pos,2i+1)=cos(\frac{pos}{10000 \frac{2i}{d_{model}}})$

其中pos是指当前词在句子中的位置，i是指向量中每个值的index，可以看出，在偶数位置，使用正弦编码，在奇数位置，使用余弦编码.

从编码公式中可以看出，给定词语的 pos，可以把它编码成一个 $d_{model}$ 的向量. 也就是说，位置编码的每一个维度对应正弦曲线，波长构成了从 $2\pi$ 到 $10000 \times 2\pi$ 的等比数列。

上面的位置编码是绝对位置编码. 但是词语的相对位置也非常重要. 这就是论文为什么要使用三角函数的原因.

正弦函数能够表达相对位置信息，主要数学依据是以下两个公式：

$sin(\alpha_\beta) = sin\alpha cos\beta + cos\alpha sin\beta$

$cos(\alpha_\beta) = cos\alpha cos\beta + sin\alpha sin\beta$

上面的公式说明，对于词汇之间的位置偏移 k, $PE(pos +k)$ 可以表示成 $PE(pos), PE(k)$ 组合的形式，相当于有了可以表达相对位置的能力.

最后把这个Positional Encoding与embedding的值相加，作为输入送到下一层

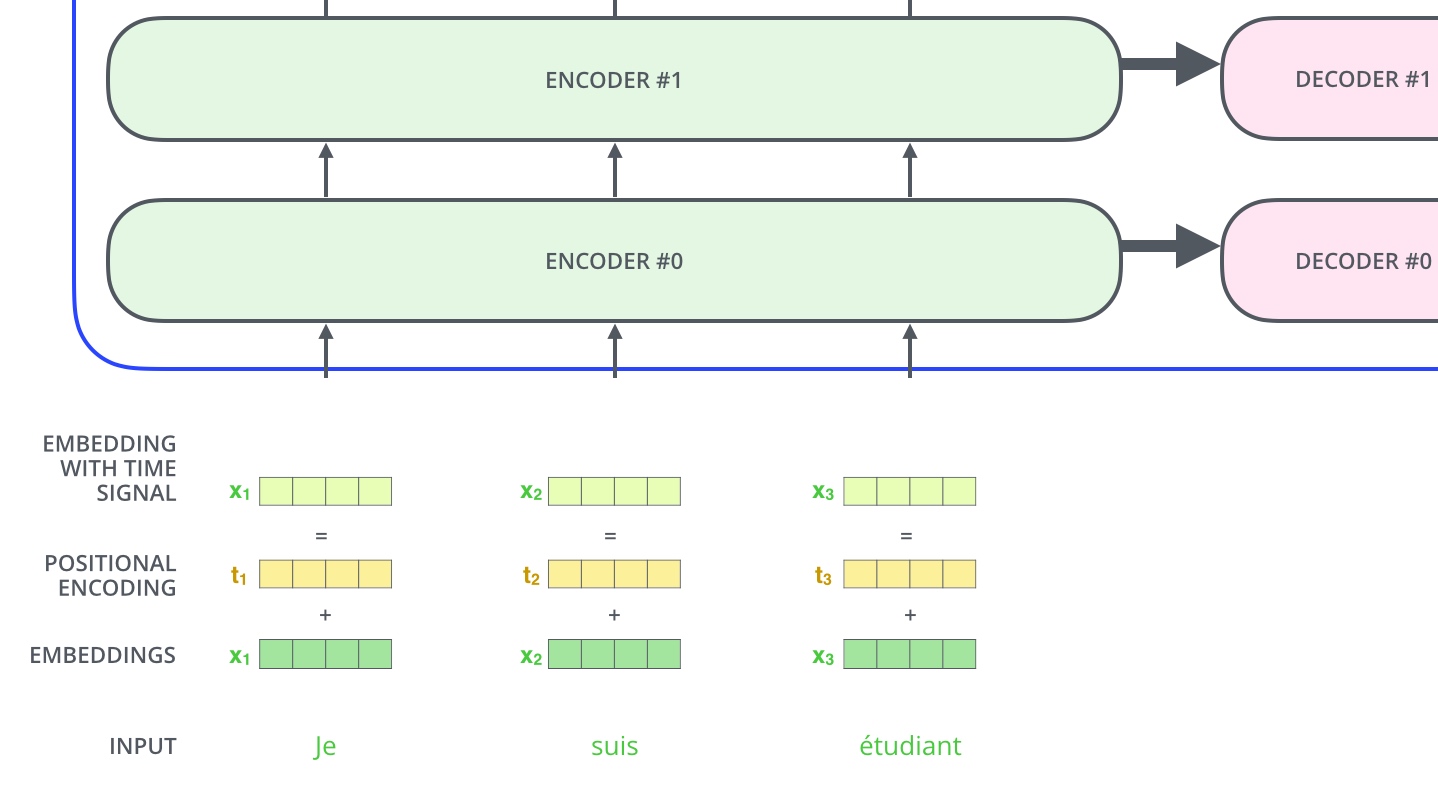
假设词嵌入的维数为4，那么实际的位置编码将如下所示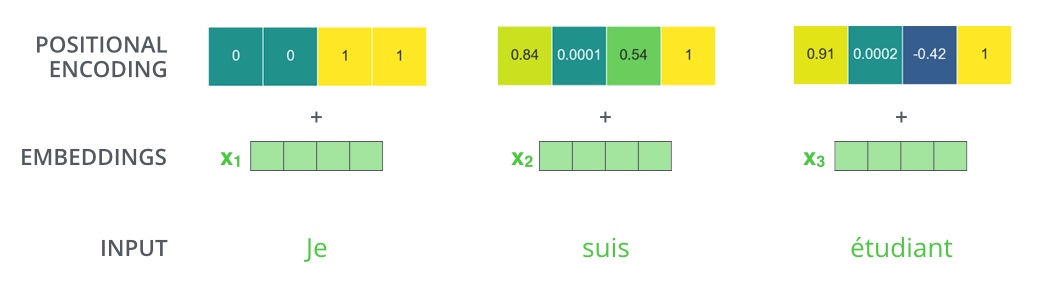： 按照公式对应计算的话应该是[0, 1, 0, 1],[0.84, 0.54, 0.0001, 1],[0.91, -0.42, 0.0002, 1],但其实代码里实现的都是将所有sin值计算完放在一起，所有cos值计算完放在一起，就变成了上图的表示

在下图中，每一行对应一个词向量的位置编码，所以第一行对应着输入序列的第一个词. 每行包含512个值，每个值介于1和-1之间. 对它们进行了颜色编码，所以图案是可见的: 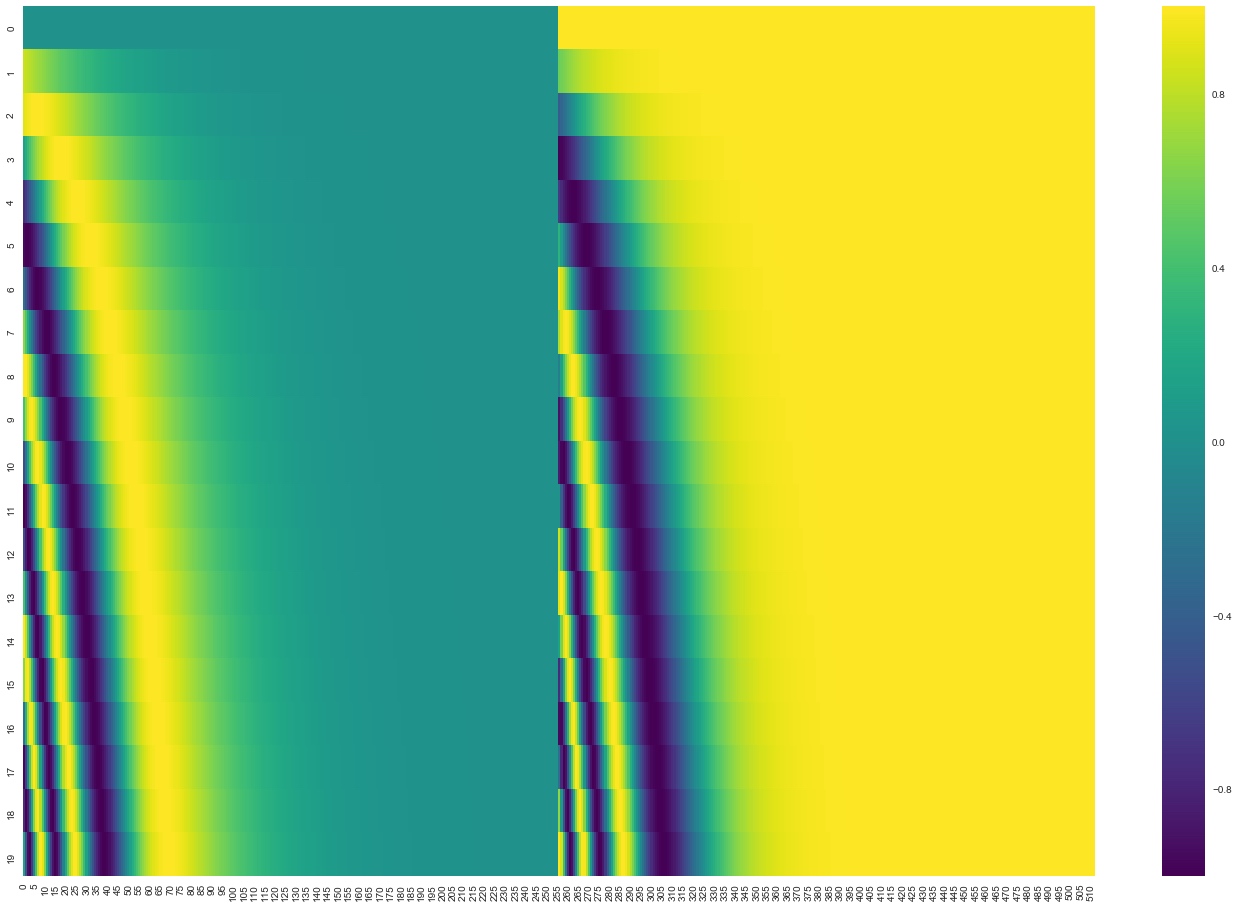(20字(行)的位置编码实例，词嵌入大小为512(列). 可以看到它从中间分裂成两半. 这是因为左半部分的值由一个函数(使用正弦)生成，而右半部分由另一个函数(使用余弦)生成. 然后将它们拼在一起而得到每一个位置编码向量)

Layer Normalization

在transformer中，每一个子层（self-attetion，ffnn）之后都会接一个残缺模块，并且有一个Layer normalization 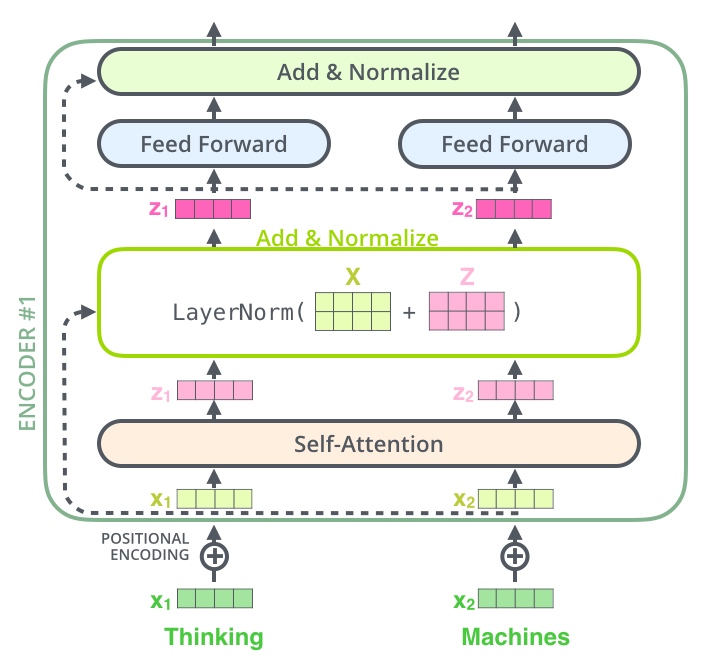其中Add代表了Residual Connection，是为了解决多层神经网络训练困难的问题，通过将前一层的信息无差的传递到下一层，可以有效的仅关注差异部分，这一方法之前在图像处理结构如ResNet等中常常用到.

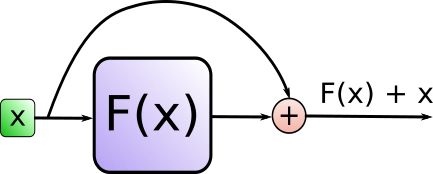
而Norm则代表了Layer Normalization，通过对层的激活值的归一化，可以加速模型的训练过程，使其更快的收敛.

具体公式如下:

$LayerNorm(x+Dropout(Sublayer(x)))$

Normalization有很多种，但是它们都有一个共同的目的，那就是把输入转化成均值为0方差为1的数据. 在把数据送入激活函数之前进行normalization（归一化), 因为不希望输入数据落在激活函数的饱和区.

Batch Normalization的主要思想就是：在每一层的每一批数据上进行归一化. 可能会对输入数据进行归一化，但是经过该网络层的作用后，数据已经不再是归一化的了. 随着这种情况的发展，数据的偏差越来越大，反向传播需要考虑到这些大的偏差，这就迫使只能使用较小的学习率来防止梯度消失或者梯度爆炸.

BN的具体做法就是对每一小批数据，在批这个方向上做归一化. 如下图所示：

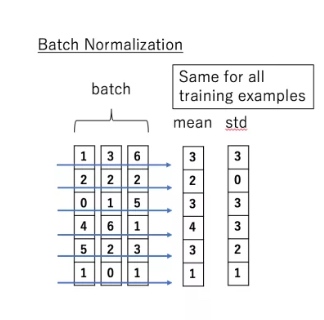
可以看到，右半边求均值是沿着数据 batch_size的方向进行的，其计算公式如下：

$BN(x_i)=α \times \frac{x_i−μ_b}{\sqrt{σ^2_B+ϵ}} + β$

Layer normalization也是归一化数据的一种方式，不过 LN 是在每一个样本上计算均值和方差，而不是BN那种在批方向计算均值和方差:

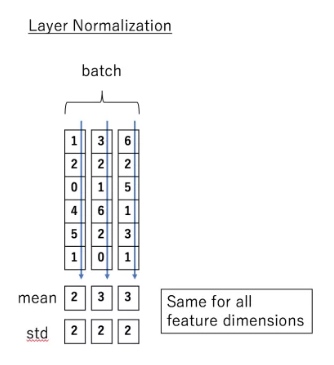
LN 的公式：

$LN(x_i)=α \times \frac{x_i−μ_L}{\sqrt{σ^2_L+ϵ}} + β$

到这里为止就是全部encoders的内容了，如果把两个encoders叠加在一起就是这样的结构

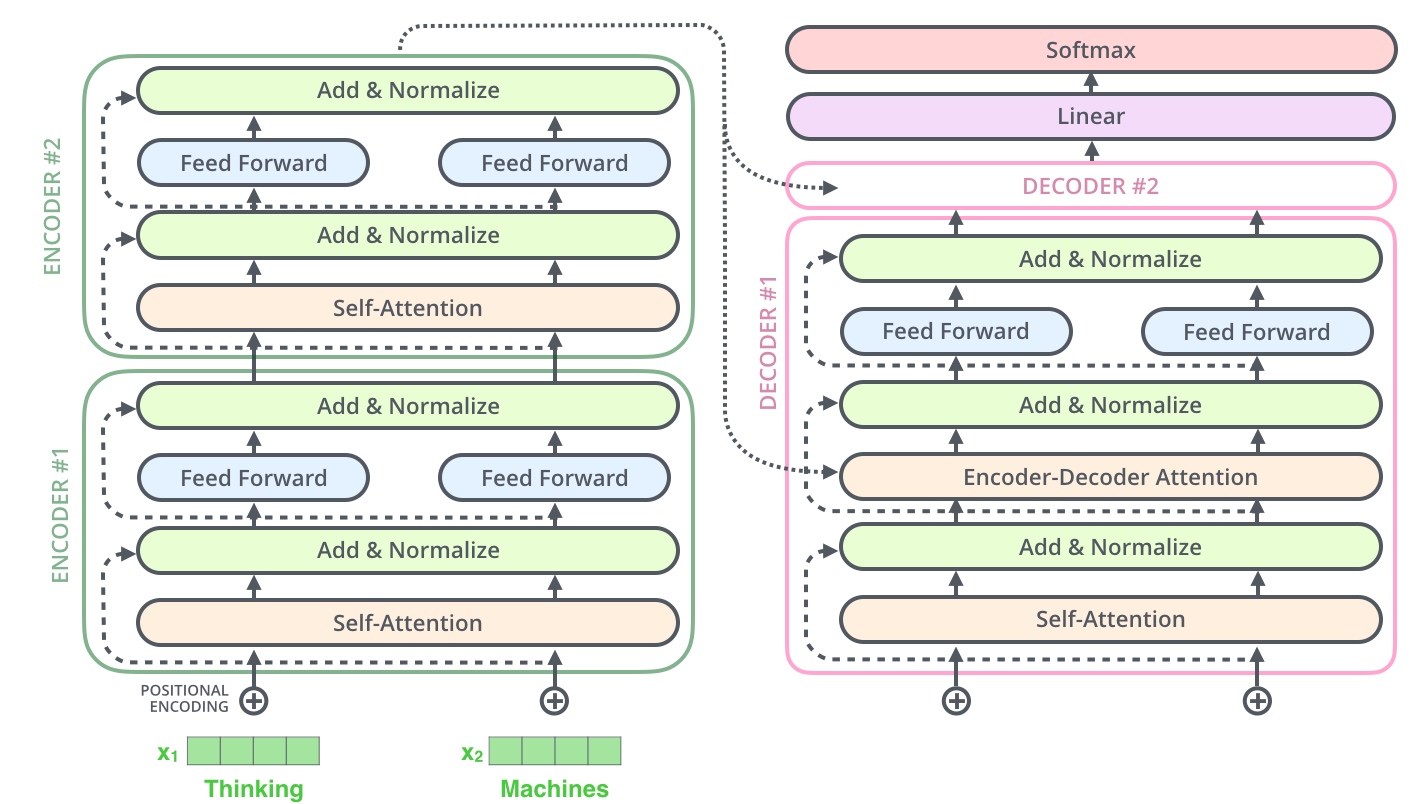
4. Decoder层

-w496 它和encoder的不同之处在于Decoder多了一个Encoder-Decoder Attention，两个Attention分别用于计算输入和输出的权值：

  1. Self-Attention：当前翻译和已经翻译的前文之间的关系
  2. Encoder-Decnoder Attention：当前翻译和编码的特征向量之间的关系

第一层的decoder (Masked Self-Attention) 的key, query, value均来自前一层decoder的输出. 但加入了Mask操作, 只能注意到前面已经翻译过的输出的词语，因为当前还并不知道下一个输出词语，这是之后才会推测到的.

第二层的decoder (encoder-decoder attention layer)，即它的query来自于之前一级的decoder层的输出，但其key和value来自于encoder的输出，这使得decoder的每一个位置都可以注意到输入序列的每一个位置.

总结一下，k和v的来源总是相同的，q在encoder及第一级decoder中与k,v来源相同，在encoder-decoder attention layer中与k,v来源不同

由于在机器翻译中，解码过程是一个顺序操作的过程，也就是当解码第 $k$ 个特征向量时，只能看到第 $k-1$ 及其之前的解码结果，论文中把这种情况下的multi-head attention叫做masked multi-head attention.

decoder部分其实和encoder部分大同小异，不过在最下面额外多了一个masked mutil-head attetion，这里的mask也是transformer一个很关键的技术

Mask

mask 表示掩码，它对某些值进行掩盖，使其在参数更新时不产生效果, 而要掩盖的值就是 token, 因为不能将attention放到它身上, 它对Encoder的输出表示(Encoder representation)不会起到作用, 对Decoder最后的预测结果也不会起到作用. Transformer 模型里面涉及两种 mask，分别是 padding mask 和 sequence mask.

其中，padding mask 在所有的 scaled dot-product attention 里面都需要用到，而 sequence mask 只有在 decoder 的 self-attention 里面用到.

Padding Mask

因为每个批次(batch)输入序列长度是不一样的也就是说, 要对输入序列进行对齐(在原句子上填充 token), 使当个批次的所有输入序列长度一致; 但是如果输入的序列太长，则是截取左边的内容，把多余的直接舍弃. 而padding mask序列就是生成一个全部都为0 (false),长度与输入序列的长度一致的序列(张量), 然后将所有非 token位置的值变成1 (true). 值为 0 (false) 的地方就是要进行处理的地方.

这些填充的位置，其实是没什么意义的，所以attention机制不应该把注意力放在这些位置上，所以需要进行一些处理. 具体的做法是，把用一个非常大的负数(负无穷)来取代这些位置上的0，这样的话，经过 softmax，这些位置的概率就会接近0.

Sequence/Subsequent mask

sequence/subsequent mask 是为了使得 decoder 不能看见未来的信息. 也就是对于一个序列，在 time_step 为 t 的时刻，Decoder输出应该只能依赖于 t 时刻之前的输出，而不能依赖 t 和 t 之后的输出. 因此需要想一个办法，把 t 之后的信息给隐藏起来.

具体做法也很简单：产生一个下三角矩阵，下三角的值全为 1，上三角的值全为0，对角线也是 1. 把这个矩阵作用在每一个序列上，就可以达到目的. E.g.: $$\begin{bmatrix} 1 & 0 & 0 \\ 1 & 1 & 0 \\ 1 & 1 & 1 \end{bmatrix}$$ 这样, 在第一行的时候就只能看到第一个token, 在第二行的时候就只能看到前两个token.

最后, 将Padding Mask和Sequence/Subsequent mask结合起来, 例如某个输入序列[‘hello’,‘world’,], 它们的mask序列就是: $$\begin{bmatrix} 1 & 0 & 0 \\ 1 & 1 & 0 \\ 1 & 1 & 0 \end{bmatrix}$$

  • 对于 decoder 的 self-attention，里面使用到的 scaled dot-product attention，同时需要padding mask 和 sequence mask 作为 attn_mask，具体实现就是两个mask相加作为attn_mask
  • 其他情况，attn_mask 一律等于 padding mask

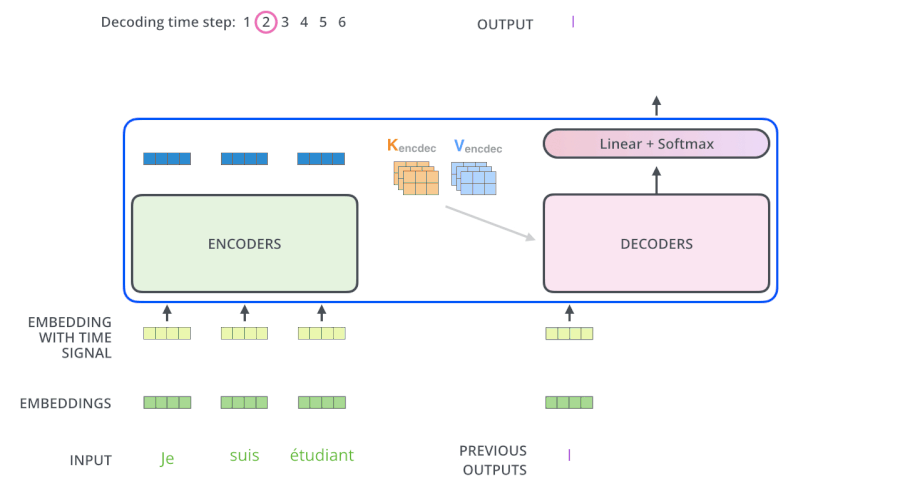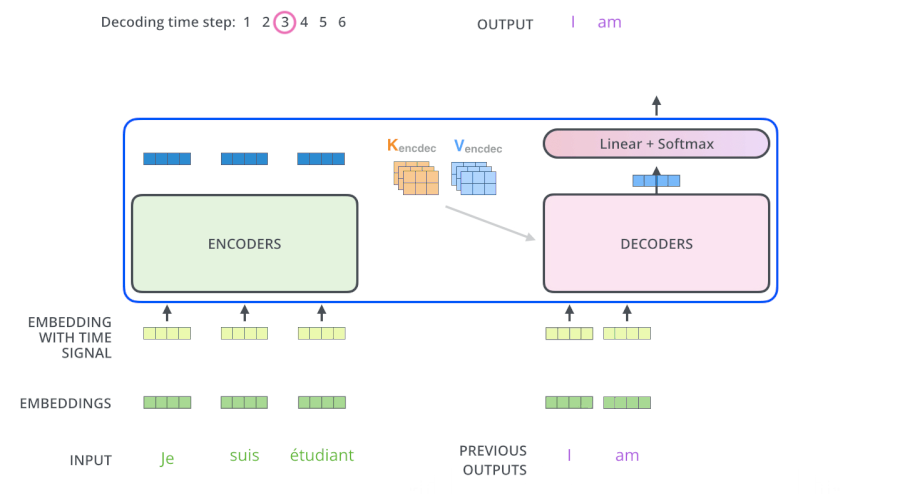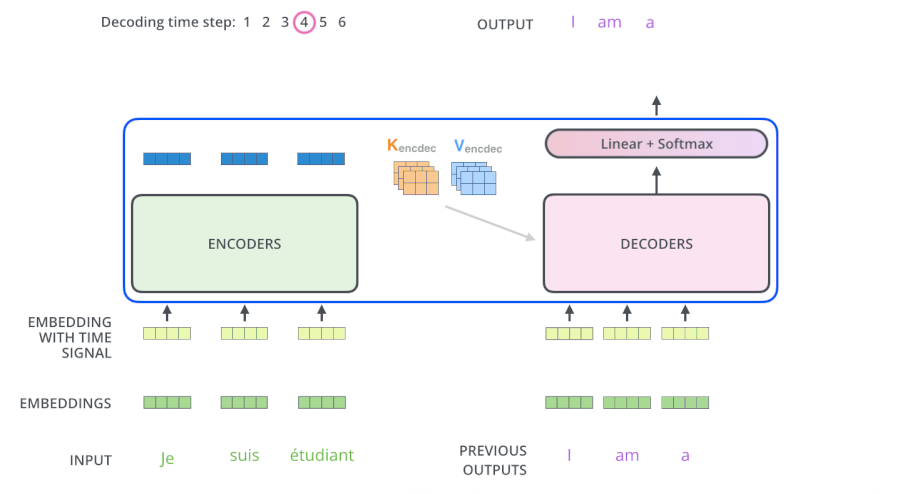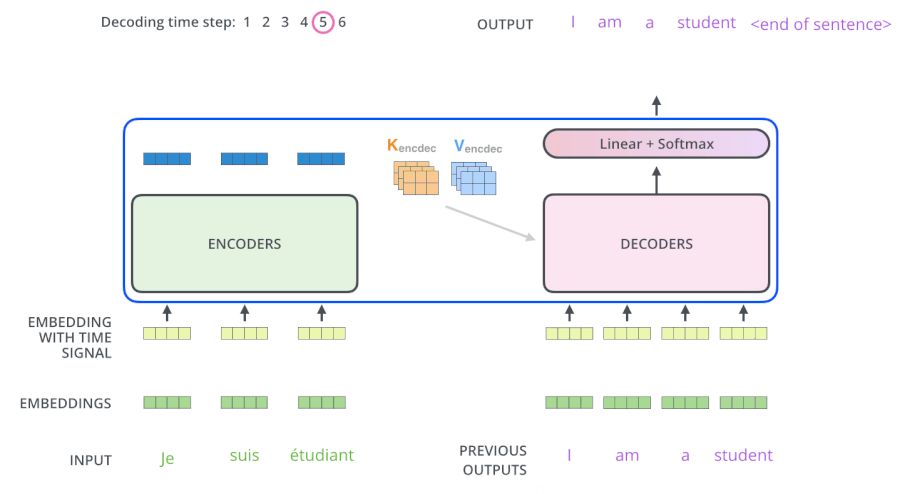
IMG_2847

5. Output层

当decoder层全部执行完毕后, 要把得到的向量映射为需要的词, 即在结尾再添加一个全连接层和softmax层. 假如词典是1w个词，那最终softmax会输入1w个词的概率，概率值最大的对应的词就是最终的结果

6. Why Self-Attention

通过分析下面三个指标：

  1. 每一层的计算复杂度
  2. 能够被并行的计算，用需要的最少的顺序操作的数量来衡量
  3. 网络中long-range dependencies的path length，在处理序列信息的任务中很重要的在于学习long-range dependencies. 影响学习长距离依赖的关键点在于前向/后向信息需要传播的步长，输入和输出序列中路径越短，那么就越容易学习long-range dependencies. 因此比较三种网络中任何输入和输出之间的最长path length

结果如下所示

并行计算

Self-Attention layer用一个常量级别的顺序操作$O(1)$，将所有的positions连接起来

Recurrent Layer需要 $O(n)$ 个顺序操作

计算复杂度分析

如果序列长度 $n$ 表示维度 $d$, Self-Attention Layer比recurrent layers快，这对绝大部分现有模型和任务都是成立的.

为了提高在序列长度很长的任务上的性能，我们对Self-Attention进行限制，只考虑输入序列中窗口为 $r$ 的位置上的信息，这称为Self-Attention(restricted), 这回增加maximum path length到 $O(n/r)$.

length path

如果卷积层kernel width $k<n$ ，并不会将所有位置的输入和输出都连接起来. 这样需要 $O(n/r)$ 个卷积层或者 $O(log_k(n))$ 个dilated convolution，增加了输入输出之间的最大path length.

卷积层比循环层计算复杂度更高，是k倍. 但是Separable Convolutions将见效复杂度.

同时self-attention的模型可解释性更好(interpretable).

优点：

  1. 虽然Transformer最终也没有逃脱传统学习的套路，Transformer也只是一个全连接（或者是一维卷积）加Attention的结合体. 但是其设计已经足够有创新，因为其抛弃了在NLP中最根本的RNN或者CNN并且取得了非常不错的效果，算法的设计非常精彩，值得每个深度学习的相关人员仔细研究和品位
  2. Transformer的设计最大的带来性能提升的关键是将任意两个单词的距离是1，这对解决NLP中棘手的长期依赖问题是非常有效的
  3. 计算复杂度低
  4. 算法的并行性非常好，符合目前的硬件（主要指GPU）环境

缺点：

  1. 粗暴的抛弃RNN和CNN虽然非常炫技，但是它也使模型丧失了捕捉局部特征的能力，RNN + CNN + Transformer的结合可能会带来更好的效果
  2. Transformer失去的位置信息其实在NLP中非常重要，而论文中在特征向量中加入Position Embedding也只是一个权宜之计，并没有改变Transformer结构上的固有缺陷

7. 训练部分总结(Optional)

在训练过程中，一个未经训练的模型会通过一个完全一样的前向传播. 但因为用有标记的训练集来训练它，所以可以用它的输出去与真实的输出做比较.

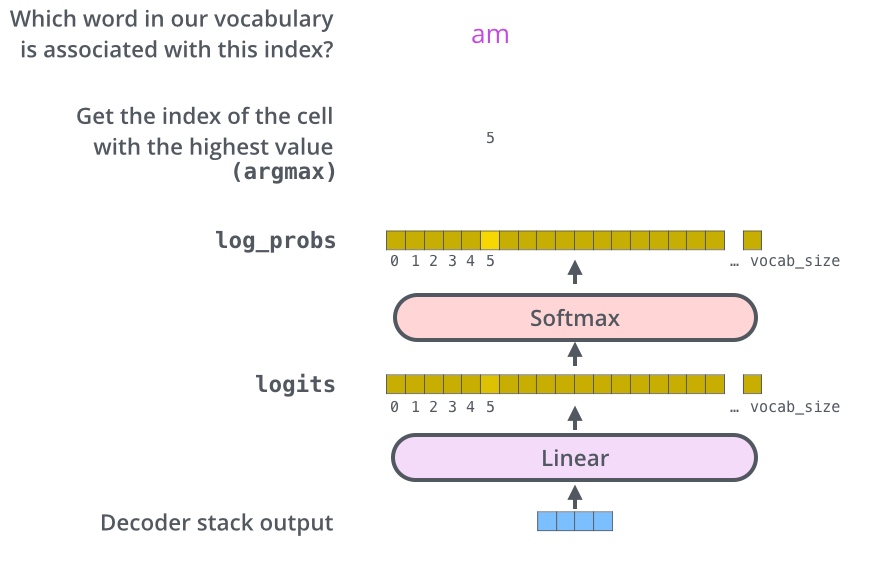
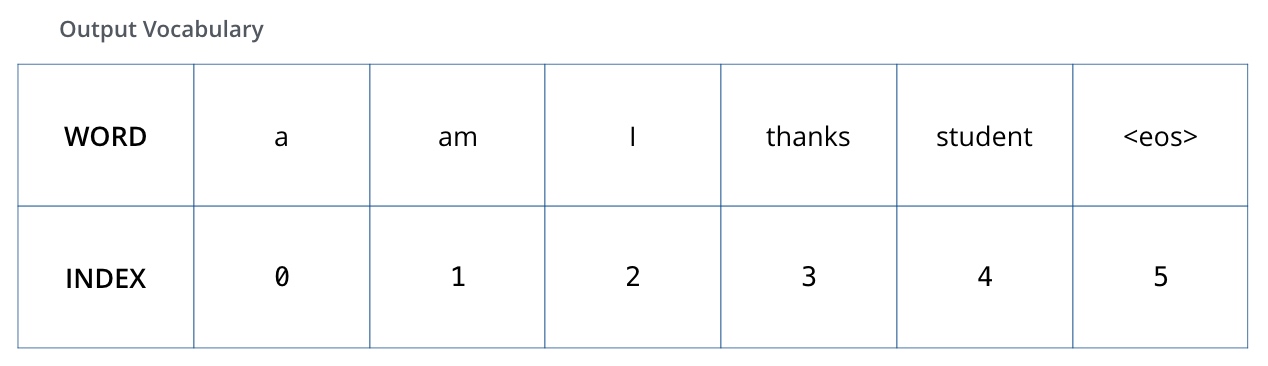
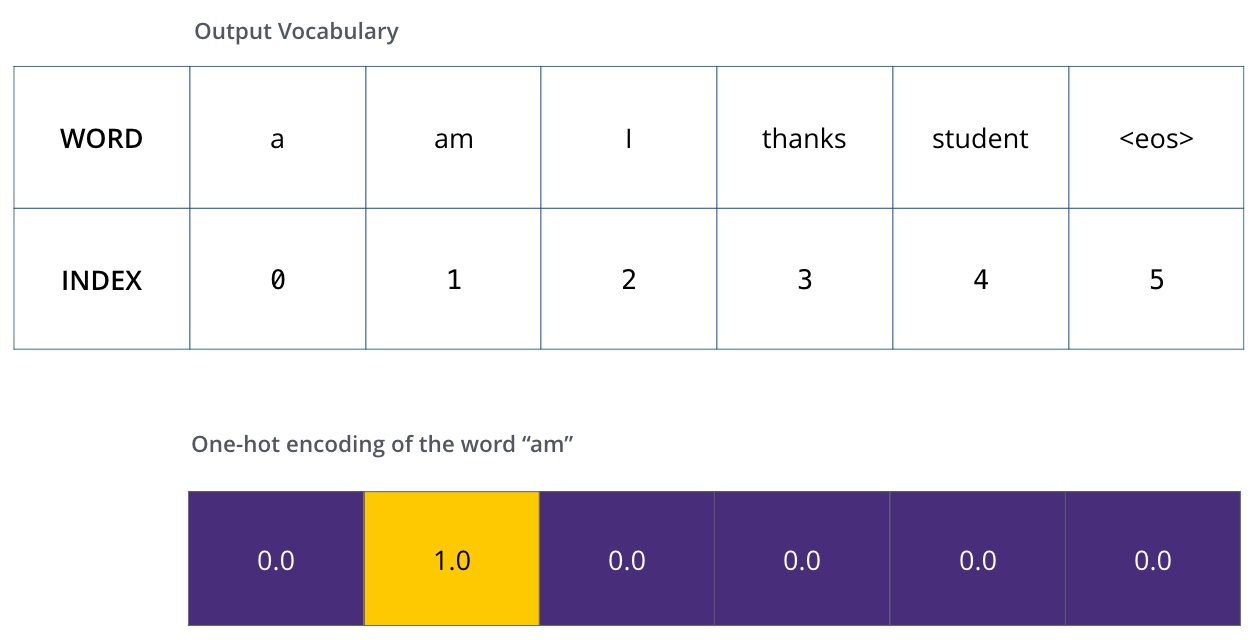
为了把这个流程可视化，假设输出词汇仅仅包含六个单词：“a”, “am”, “i”, “thanks”, “student”以及 “”（end of sentence的缩写形式）

一旦定义了输出词表，可以使用一个相同宽度的向量来表示词汇表中的每一个单词. 这也被认为是一个one-hot 编码. 所以，可以用下面这个向量来表示单词“am”：

损失函数

模型的损失函数——这是用来在训练过程中优化的标准. 通过它可以训练得到一个结果尽量准确的模型.

比如说正在训练模型，现在是第一步，一个简单的例子——把“merci”翻译为“thanks”.

这意味着想要一个表示单词“thanks”概率分布的输出. 但是因为这个模型还没被训练好，所以不太可能现在就出现这个结果. 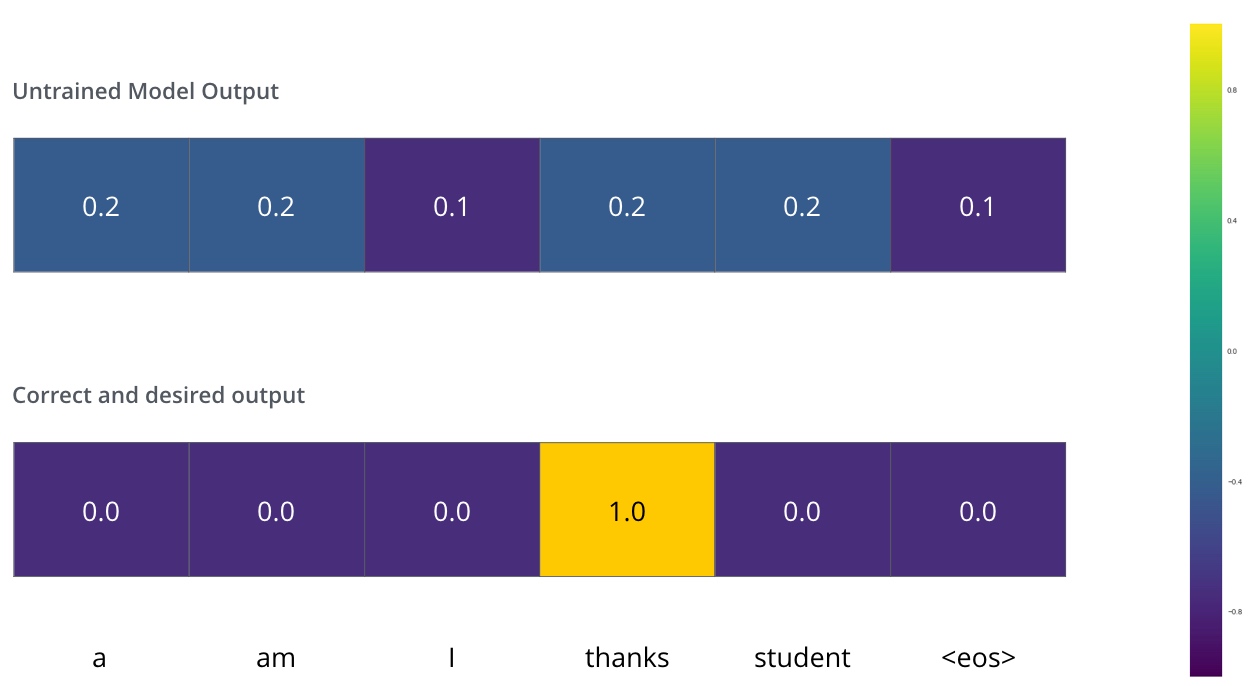(因为模型的参数（权重）都被随机的生成，（未经训练的）模型产生的概率分布在每个单元格/单词里都赋予了随机的数值。可以用真实的输出来比较它，然后用反向传播算法来略微调整所有模型的权重，生成更接近结果的输出)

比较两个概率分布的方法: 简单地用其中一个减去另一个. 更多细节请参考交叉熵和KL散度.

这是一个过于简化的例子. 更现实的情况是处理一个句子, 例如，输入“je suis étudiant”并期望输出是“i am a student”. 那希望模型能够成功地在这些情况下输出概率分布：

  • 每个概率分布被一个以词表大小（我们的例子里是6，但现实情况通常是3000或10000）为宽度的向量所代表。
  • 第一个概率分布在与“i”关联的单元格有最高的概率
  • 第二个概率分布在与“am”关联的单元格有最高的概率
  • 以此类推，第五个输出的分布表示“”关联的单元格有最高的概率

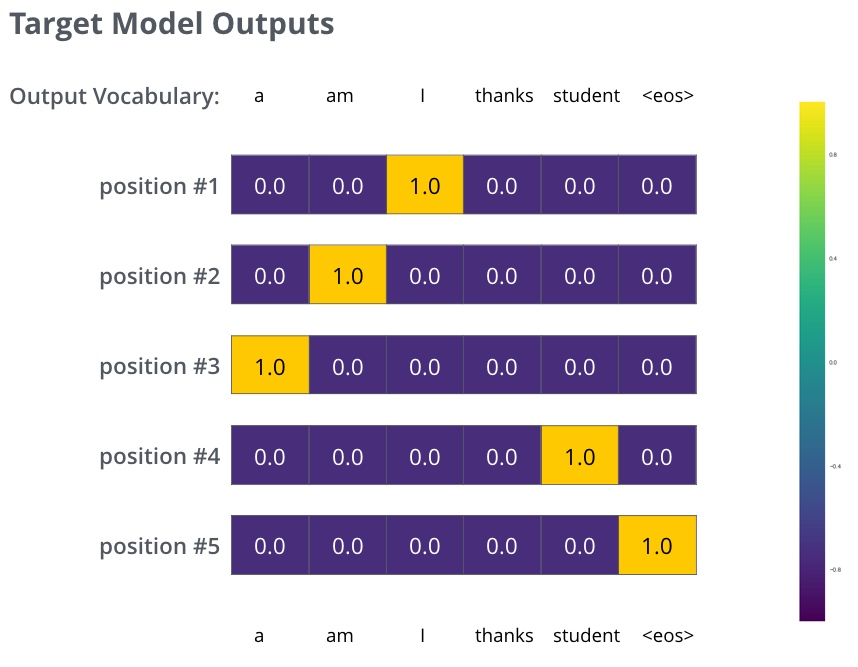(依据例子训练模型得到的目标概率分布)

在一个足够大的数据集上充分训练后，我们希望模型输出的概率分布看起来像这个样子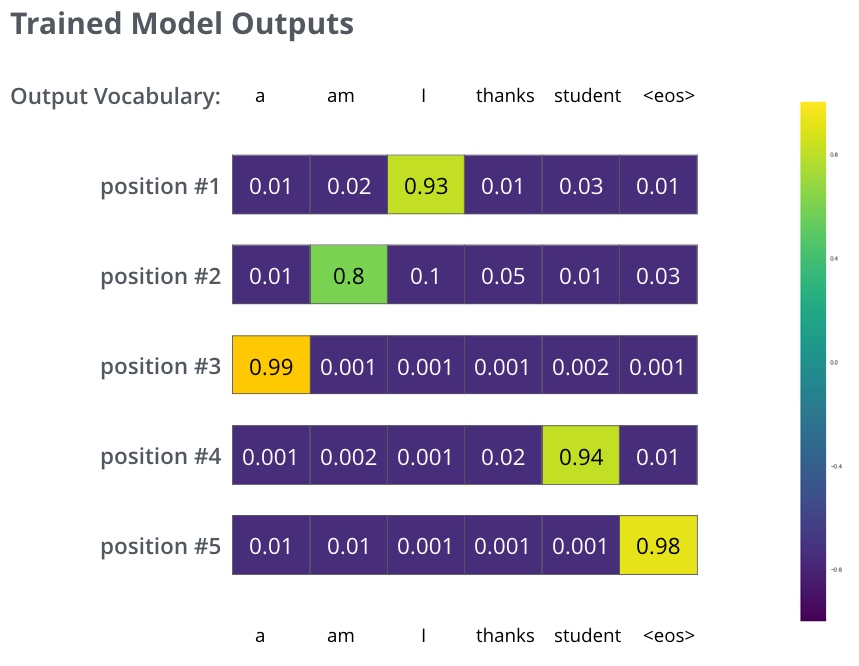： (期望训练过后，模型会输出正确的翻译. 当然如果这段话完全来自训练集，它并不是一个很好的评估指标（参考交叉验证. 注意到每个位置（词）都得到了一点概率，即使它不太可能成为那个时间步的输出——这是softmax的一个很有用的性质，它可以帮助模型训练)

因为这个模型一次只产生一个输出，不妨假设这个模型只选择概率最高的单词，并把剩下的词抛弃. 这是其中一种方法（叫贪心解码). 另一个完成这个任务的方法是留住概率最靠高的两个单词（例如I和a），那么在下一步里，跑模型两次：其中一次假设第一个位置输出是单词“I”，而另一次假设第一个位置输出是单词“me”，并且无论哪个版本产生更少的误差，都保留概率最高的两个翻译结果. 然后为第二和第三个位置重复这一步骤. 这个方法被称作集束搜索（beam search). 在例子中，集束宽度是2（因为保留了2个集束的结果，如第一和第二个位置），并且最终也返回两个集束的结果（top_beams也是2). 这些都是可以提前设定的参数.

8. Reference