LeetCode Template
Ref:
- https://blog.csdn.net/fuxuemingzhu/article/details/101900729
- https://www.youtube.com/user/xxfflower/videos
- https://github.com/TheAlgorithms/Python/blob/master/DIRECTORY.md
一些典型的题目，记住其写法，理解其思想，即可做到一通百通
二分查找
- 二分查找即搜索过程从数组的中间元素开始
- 如果中间元素正好是要查找的元素,则搜索过程结束
- 如果中间元素大于或小于要查找元素,则在小于或大于中间元素的那一半进行搜索,而且跟开始一样从中间元素开始比较
- 如果在某一步骤数组为空,则代表找不到
- 这种算法每一次比较都会使搜索范围缩小一半
- 条件:
- 要是有序的，因为二分查找操作的是下标，所以要求是顺序的
- 最优时间复杂度：O(1), 最坏时间复杂度：O(logn)
- 区间定义:
[l,r}左闭右开 E.g.2 ≤ i < 13(Python 的 Range 就是左闭右开)
最基本的二分查找
非递归(循环)二分查找
def binary_chop(arr, target):
r = len(arr)-1
l = 0
while l <= r:
mid = l + (r-l) // 2
if arr[mid] == target:
return mid
elif arr[mid] > target:
r = mid - 1
else:
l = mid + 1
return -1注意:
- 循环的判定条件是：low <= high
- 为了防止数值溢出，mid = low + (high - low)/2 这里有具体解释
- 当 arr[mid]不等于target时，high = mid - 1或low = mid + 1
递归二分查找
def binary_chop1(arr, target):
r = len(arr)
l = 0
if r < 1:
return -1
mid = l // 2
if arr[mid] == target:
return mid
elif arr[mid] > target:
return binary_chop1(arr[0:mid],target)
else:
return binary_chop1(arr[mid+1:],target)查找目标值区域的边界
lower bound: 查找目标值区域的左边界 / 查找与目标值相等的第一个位置 / 查找第一个不小于目标值数的位置
A = [1,3,3,5, 7 ,7,7,7,8,14,14]
target = 7
return 4def binarySearchLowerBound(A, target):
low,high = 0,len(A)-1
while low <= high:
mid = low + (high - low) // 2
if A[mid] >= target:
high = mid - 1
else:
low = mid + 1
if low < A.length and A[low] == target:
return low
else
return -1upper bound: 查找目标值区域的右边界 / 查找与目标值相等的最后一个位置 / 查找最后一个不大于目标值数的位置
A = [1,3,3,5,7,7,7, 7 ,8,14,14]
target = 7
return 7def binarySearchUpperBound(A, target):
low,high = 0,len(A)-1
while low <= high:
mid = low + (high - low) // 2
if A[mid] <= target:
low = mid + 1
else:
high = mid - 1
if high > -1 and A[low] == target:
return high
else
return -1在旋转数组中查找最小元素
查找旋转数组的最小元素（假设不存在重复数字）
def findMin(nums):
if len(nums) == 0:
return -1
left,right = 0,len(nums) - 1
while left < right:
mid = left + (right - left) // 2
if nums[mid] > nums[right]:
left = mid + 1
else:
right = mid
return nums[left]和之前的二分查找的几点区别：
- 循环判定条件为left < right，没有等于号
- 循环中，通过比较nums[left]与num[mid]的值来判断mid所在的位置:
- 如果nums[mid] > nums[right]，说明前半部分是有序的，最小值在后半部分，令left = mid + 1
- 如果nums[mid] <= num[right]，说明最小值在前半部分，令right = mid
- 最后，left会指向最小值元素所在的位
查找旋转数组的最小元素（假设存在重复数字）
def findMin(nums):
if len(nums) == 0
return -1
left,right = 0,len(nums) - 1
while left < right:
mid = left + (right - left) // 2
if nums[mid] > nums[right]:
left = mid + 1
elif nums[mid] < nums[right]:
right = mid
else:
right-=1
return nums[left]- 如果nums[mid] > nums[right], 说明最小值在后半部分(旋转部分)
- 如果nums[mid] < nums[right], 说明最小值在前半部分(有序部分)
- 和之前不存在重复项的差别是:
- 当nums[mid] == nums[right]时，不能确定最小值在 mid的左边还是右边，所以就让右边界减一
在旋转排序数组中搜索
在旋转排序数组中搜索并返回目标元素的下标（不考虑重复项）
没有必要找到旋转数组的分界点，对于搜索左侧还是右侧, 是可以根据mid跟high的元素大小来判定出来的，直接根据target的值做二分搜索就可以了
def search(self, nums: List[int], target: int) -> int:
if len(nums) == 0:
return -1
left,right=0,len(nums)-1
while left<=right:
mid=left+(right-left)//2
if nums[mid] == target:
return mid
elif nums[left] <= nums[mid]:
if target < nums[mid] and target >= nums[left]:
right = mid - 1
else:
left = mid + 1
elif nums[mid] <= nums[right]:
if target > nums[mid] and target <= nums[right]:
left = mid + 1
else:
right = mid - 1
return -1在旋转排序数组中搜索并返回目标元素的下标（考虑重复项）
def search(self, nums: List[int], target: int) -> int:
if len(nums) == 0:
return -1
left,right=0,len(nums)-1
while left<=right:
mid=left+(right-left)//2
if nums[mid] == target:
return mid
elif nums[mid] > nums[right]:
if target < nums[mid] and target >= nums[left]:
right = mid
else:
left = mid + 1
elif nums[mid] < nums[right]:
if target > nums[mid] and target <= nums[right]:
left = mid + 1
else:
right = mid
else:
right-=1
return -1二维数组中的查找
二维数组是有序的，从右上角来看，向左数字递减，向下数字递增. 因此可以利用二分查找的思想，从右上角出发：
- 当要查找数字比右上角数字大时，下移
- 当要查找数字比右上角数字小时，左移
- 如果出了边界，则说明二维数组中不存在该整数
code:
def findNumberIn2DArray(self, matrix: List[List[int]], target: int) -> bool:
if not matrix: return False
i, j = len(matrix) - 1, 0
while i >= 0 and j < len(matrix[0]):
if matrix[i][j] > target: i -= 1
elif matrix[i][j] < target: j += 1
else: return True
return Falseref: https://www.jianshu.com/p/12035a972bdb
链表
class ListNode:
def __init__(self, x):
self.val = x
self.next = None
def __repr__(self):
return "ListNode(val:{}, next:ListNone({}))".format(str(self.val),self.next)
head = ListNode(1)
l2 = ListNode(2)
l3 = ListNode(3)
l4 = ListNode(4)
l5 = ListNode(5)
head.next = l2
l2.next = l3
l3.next = l4
l4.next = l5
# print(l4) # ListNode(val:4, next:ListNone(ListNode(val:5, next:ListNone(None))))快慢指针
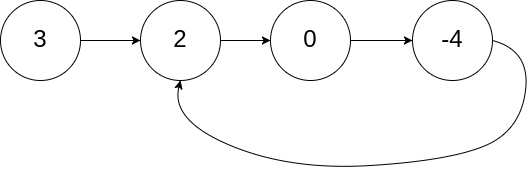
好像两个人在一个操场上跑步,速度快的人一定会和速度慢的相遇(环) (但可能会多跑几圈). 下面的例子是检测链表是否有环.
def hasCycle(head):
"""
:type head: ListNode
:rtype: bool
"""
slow = head
fast = head
while fast and fast.next:
slow = slow.next # 它跑一步
fast = fast.next.next # 它跑两部
if slow == fast:
return True
return False空间复杂度O(1);
反转链表
class Node(object):
def __init__(self, data, next=None):
self.val = data
self.next = next
def rev(head):
# 将原链表的第一个节点变成了新链表的最后一个节点，同时将原链表的第二个节点保存在cur中
prev = head
cur = head
prev.next = None
while cur:
# 从原链表的第二个节点开始遍历到最后一个节点，将所有节点翻转一遍
temp = cur.next
cur.next = prev
prev =cur
cur = temp
return prev
if __name__ == '__main__':
link = Node(1, Node(2, Node(3, Node(4, Node(5, Node(6, Node(7, Node(8, Node(9)))))))))
root = rev(link)
while root:
print(root.data)
root =root.next简单写法:
def reverseList(head: ListNode) -> ListNode:
# print(head) # ListNode{val: 1, next: ListNode{val: 2, next: ListNode{val: 3, next: ListNode{val: 4, next: ListNode{val: 5, next: None}}}}}
if not head: return None
prev = None
cur = head
while cur:
print(prev, '-----')
'''
None -----
ListNode{val: 1, next: None} -----
ListNode{val: 2, next: ListNode{val: 1, next: None}} -----
ListNode{val: 3, next: ListNode{val: 2, next: ListNode{val: 1, next: None}}} -----
ListNode{val: 4, next: ListNode{val: 3, next: ListNode{val: 2, next: ListNode{val: 1, next: None}}}} -----
'''
cur.next, prev, cur = prev, cur, cur.next
return prev递归写法:
def reverseList(head: ListNode) -> ListNode:
if not head or not head.next:
return head
nextNode = self.reverseList(head.next)
head.next.next = head
head.next = None
return nextNode排序
BFS
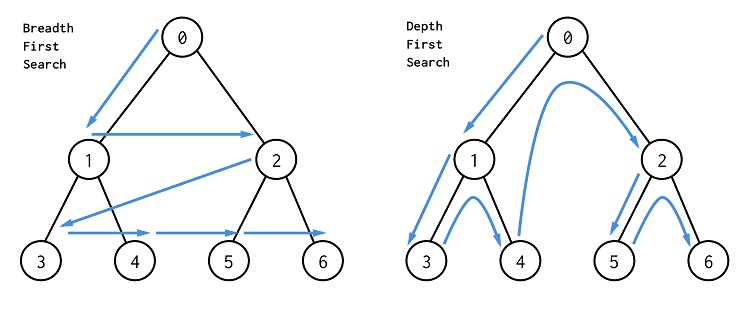
BFS模板1 - 不需要确定当前遍历到了哪一层 (无需分层遍历):
while queue 不空：
cur = queue.pop()
for 节点 in cur的所有相邻节点：
if 该节点有效且未访问过：
queue.push(该节点)BFS模板2 - 要确定当前遍历到了哪一层 (需要分层遍历):
这里增加了level表示当前遍历到二叉树中的哪一层了，也可以理解为在一个图中，现在已经走了多少步了。size表示在当前遍历层有多少个元素，也就是队列中的元素数，把这些元素一次性遍历完，即把当前层的所有元素都向外走了一步.
level = 0
while queue 不空：
size = queue.size()
while (size --) {
cur = queue.pop()
for 节点 in cur的所有相邻节点：
if 该节点有效且未被访问过：
queue.push(该节点)
}
level ++;针对树的BFS
无需分层遍历
from collections import deque
# Definition for a binary tree node.
class TreeNode:
def __init__(self, x):
self.val = x
self.left = None
self.right = None
def level_order_tree(root):
if not root:
return
# 这里借助python的双向队列实现队列
# 避免使用list.pop(0)出站的时间复杂度为O(n)
queue = deque([root])
result = []
while queue:
node = queue.popleft()
# do somethings
result.append(node.val)
if node.left:
queue.append(node.left)
if node.right:
queue.append(node.right)
return result需要分层遍历
def level_order_tree(root):
if not root:
return
q = [root]
while q:
new_q = []
for node in q:
# do somethins with this layer nodes...
# 判断左右子树
if node.left:
new_q.append(node.left)
if node.right:
new_q.append(node.right)
# 记得将旧的队列替换成新的队列
q = new_q
# 最后return想要返回的东西
return xxx针对图的BFS
无需分层遍历
from collections import deque
def bsf_graph(root):
if not root:
return
# queue和seen为同时出现
queue = deque([root])
# seen避免图遍历过程中重复访问的情况，导致无法跳出循环
seen = set([root])
while queue:
head = queue.popleft()
# do somethings with the head node
# 将head的邻居都添加进来
for neighbor in head.neighbors:
if neighbor not in seen:
queue.append(neighbor)
seen.add(neighbor)
return xxx需要分层遍历
def bsf_graph(root):
if not root:
return
queue = [root]
seen = set([root])
while queue:
new_queue = []
for node in queue:
# do somethins with the node
for neighbor in node.neighbors:
if neighbor not in seen:
new_queue.append(neighbor)
seen.add(neighbor)
return xxxDFS
回溯法
树
递归
迭代
前/中/后序遍历
使用递归的三种树的遍历方法
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None先序遍历：根左右
def preorderTraversal(self, root: TreeNode) -> List[int]: def helper(node): if not node: return [] return [node.val]+helper(node.left)+helper(node.right) return helper(root)中序遍历：左根右
def inorderTraversal(self, root: TreeNode) -> List[int]: def helper(node): if not node: return [] return helper(node.left)+[node.val]+helper(node.right) return helper(root)后序遍历：左右根
def postorderTraversal(self, root: TreeNode) -> List[int]: def helper(node): if not node: return [] return helper(node.left)+helper(node.right)+[node.val] return helper(root)层序遍历: 宽度优先遍历. 在同一层结点中，以从左到右的顺序依次访问 (递归函数需要有一个参数level，该参数表示当前结点的层数。遍历的结果返回到一个二维列表sol=[[]]中，sol中的每一个子列表保存了对应index层的从左到右的所有结点value值)
def levelOrder(self, root: TreeNode) -> List[int]: def helper(node, level): if not node: return else: sol[level-1].append(node.val) if len(sol) == level: # 遍历到新层时，只有最左边的结点使得等式成立 sol.append([]) helper(node.left, level+1) helper(node.right, level+1) sol = [[]] helper(root, 1) return sol[:-1]
栈结构+DFS (非递归)
二叉树的遍历都可以借助栈结构使用DFS算法完成.
最简单的先序遍历，父>左>右
- 每次入栈前先将父节点加入结果列表，然后左节点入栈
当左子树遍历完后，再遍历右子树
def preorderTraversal(self, root: TreeNode) -> List[int]: res = [] #结果列表 stack = [] #辅助栈 cur = root #当前节点 while stack or cur: while cur: #一直遍历到最后一层 res.append(cur.val) stack.append(cur) cur = cur.left top = stack.pop() #此时该节点的左子树已经全部遍历完 cur = top.right #对右子树遍历 return res
后序遍历，左>右>父
- 将上面的顺序翻转过来得到，父>右>左
所以现在可以按照之前的方法遍历，最后把结果翻转一下
def postorderTraversal(self, root: TreeNode) -> List[int]: res = [] stack = [] cur = root while stack or cur: while cur: res.append(cur.val) stack.append(cur) cur = cur.right #先将右节点压栈 top = stack.pop() #此时该节点的右子树已经全部遍历完 cur = top.left #对左子树遍历 return res[::-1] #结果翻转
中序遍历， 左>父>右
与先序遍历不同的是，出栈时才将结果写入列表
def inorderTraversal(self, root: TreeNode) -> List[int]: res = [] stack = [] cur = root while stack or cur: while cur: stack.append(cur) cur = cur.left top = stack.pop() #此时左子树遍历完成 res.append(top.val) #将父节点加入列表 cur = top.right #遍历右子树 return res
层序遍历
- 层序遍历就是按照层次由左向右输出
算法思想 - 利用队列 (因为每一层都需要从左往右打印，而每打印一个结点都会在队列中依次添加其左右两个子结点，每一层的顺序都是一样的，故必须采用先进先出的数据结构)
def levelOrder(self, root: TreeNode) -> List[int]: if not root: return [] sol = [] curr = root queue = [curr] while queue: curr = queue.pop(0) sol.append(curr.val) if curr.left: queue.append(curr.left) if curr.right: queue.append(curr.right) return sol
Code in C# and explain
Input: [1,2,3,4,5,null,null,null,null,6]
simple diagram:
1
2 3
4 5
6
detail diagram:
1
2 3
4 5 n n
n n 6 n- inorder - output: 4 2 6 5 1 3 左>父>右
- node.left push into stack till bottom.
- node4.left eq null, so pop node4, then store node4.data,
- node4.right eq null, so pop node2(if not null, then push till null), store node2.data.
- push node5, push node6,
- node6.left eq null, so pop node6, store node6.data,
- node6.right eq null, so pop node5, store node5.data
- node5.right eq null, so pop node1, store node1.data
- node1.right(node3) push into stack
- …
- preorder - output: 1 2 4 5 6 3 (父>左>右)
- push node.left into stack till bottpm, and store node.data at the same time
- node4.left eq null, so pop node4
- node4.right eq null, so pop node2
- push node5, store node5.data; push node6, store node6.data
- node6.left eq null, so pop node6
- node6.right eq null, so pop node5
- node5.right eq null, so pop node1
- push node1.right(node3), store node3.data
- …
postorder - output: 4 6 5 2 3 1 (左>右>父)
- preorder是父>左>右, 可以按照preorder的方式遍历, 但是是遍历 父>右>左 先
- 最后把结果翻转一下, 就变回左>右>父
levelorder - output: 1 2 3 4 5 6
C# code
//// PREORDER
/**
* Definition for a binary tree node.
* public class TreeNode {
* public int val;
* public TreeNode left;
* public TreeNode right;
* public TreeNode(int x) { val = x; }
* }
*/
public class Solution {
IList<int> res = new List<int>();
public IList<int> PreorderTraversal(TreeNode root) {
//// 递归
// if (root != null){
// res.Add(root.val);
// PreorderTraversal(root.left);
// PreorderTraversal(root.right);
// }
// return res;
//// 遍历
Stack<TreeNode> st = new Stack<TreeNode>();
TreeNode cur = root;
while (cur != null || st.Count != 0){
while (cur != null){
res.Add(cur.val);
st.Push(cur);
cur = cur.left;
}
cur = st.Pop();
cur = cur.right;
}
return res;
}
}
//// POSTORDER
/**
* Definition for a binary tree node.
* public class TreeNode {
* public int val;
* public TreeNode left;
* public TreeNode right;
* public TreeNode(int x) { val = x; }
* }
*/
public class Solution {
IList<int> res = new List<int>();
public IList<int> PostorderTraversal(TreeNode root) {
//// 递归
// if (root != null){
// PostorderTraversal(root.left);
// PostorderTraversal(root.right);
// res.Add(root.val);
// }
// return res;
//// 遍历
Stack<TreeNode> st = new Stack<TreeNode>();
TreeNode cur = root;
while(cur != null || st.Count != 0){
while(cur != null){
res.Add(cur.val);
st.Push(cur);
cur = cur.right;
}
cur = st.Pop();
cur = cur.left;
}
int[] array = res.ToArray();
int temp;
int count = array.Length;
for (int i = 0; i < count/2; i++)
{
temp = array[count - 1 - i];
array[count - 1 - i] = array[i];
array[i] = temp;
}
return array;
}
}
//// INORDER
/**
* Definition for a binary tree node.
* public class TreeNode {
* public int val;
* public TreeNode left;
* public TreeNode right;
* public TreeNode(int x) { val = x; }
* }
*/
public class Solution {
IList<int> res = new List<int>();
public IList<int> InorderTraversal(TreeNode root) {
//// 递归
// Console.WriteLine("Root {0}",root);
// if (root != null){
// InorderTraversal(root.left);
// res.Add(root.val);
// InorderTraversal(root.right);
// }
// return res;
//// 遍历
Stack<TreeNode> st = new Stack<TreeNode>();
TreeNode cur = root;
while (st.Count != 0 || cur != null){
// 一直遍历左边先
while (cur != null){
st.Push(cur);
// res.Add(cur.val);
cur = cur.left;
}
// 左边节点遍历完成
cur = (TreeNode)st.Pop();
res.Add(cur.val);
cur = cur.right;
}
return res;
}
}
//// LEVELORDER
/**
* Definition for a binary tree node.
* public class TreeNode {
* public int val;
* public TreeNode left;
* public TreeNode right;
* public TreeNode(int x) { val = x; }
* }
*/
public class Solution {
List<IList<int>> res = new List<IList<int>>();
public IList<IList<int>> LevelOrder(TreeNode root) {
//// 递归
// if(root==null) return res;
// int lvl = 0;
// helper(lvl, root);
// return res;
// void helper(int level,TreeNode node){
// if (node != null){
// if (level == res.Count){
// res.Add(new List<int>());
// }
// res[level].Add(node.val);
// if (node.left != null) helper(level+1, node.left);
// if (node.right != null) helper(level+1, node.right);
// }
// return;
// }
//// 遍历
if (root ==null) return res;
Queue<TreeNode> queue = new Queue<TreeNode>();
queue.Enqueue(root); // 把root放入队列
while (queue.Count !=0){
int count = queue.Count; // 当前队列node的个数 (当前一行有多少个node)
List<int> temp = new List<int>(); // 新建临时列表
for(int i=0; i< count;i++){ // 循环当前队列所有node
var tmp = queue.Dequeue(); // 从队列弹出
temp.Add(tmp.val); // 添加到临时列表
if (tmp.left != null) queue.Enqueue(tmp.left); //判断是否有下一行, 有的话添加进队列
if (tmp.right != null) queue.Enqueue(tmp.right);
}
res.Add(temp);
}
return res;
}
}
构建完全二叉树
完全二叉树是每一层（除最后一层外）都是完全填充（即，节点数达到最大）的，并且所有的节点都尽可能地集中在左侧
设计一个用完全二叉树初始化的数据结构 CBTInserter，它支持以下几种操作：
- CBTInserter(TreeNode root) 使用头节点为 root 的给定树初始化该数据结构
- CBTInserter.insert(int v) 向树中插入一个新节点，节点类型为 TreeNode，值为 v . 使树保持完全二叉树的状态，并返回插入的新节点的父节点的值
- CBTInserter.get_root() 将返回树的头节点
示例 1：
输入：inputs = ["CBTInserter","insert","get_root"], inputs = [[[1]],[2],[]]
输出：[null,1,[1,2]]示例 2：
输入：inputs = ["CBTInserter","insert","insert","get_root"], inputs = [[[1,2,3,4,5,6]],[7],[8],[]]
输出：[null,3,4,[1,2,3,4,5,6,7,8]]
初始化:
1
2 3
4 5 4
插入7:
1
2 3
4 5 4 7 会return 3, 因为其父节点是3
插入:
1
2 3
4 5 4 7
8 会return 4, 因为其父节点是4完全二叉树是每一层都满的，因此找出要插入节点的父节点是很简单的. 如果用数组tree保存着所有节点的层次遍历，那么新节点的父节点就是tree[(N -1)/2]，N是未插入该节点前的树的元素个数
构建树的时候使用层次遍历，也就是BFS把所有的节点放入到tree里。插入的时候直接计算出新节点的父亲节点。获取root就是数组中的第0个节点
时间复杂度是O(N)，空间复杂度是O(N)
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class CBTInserter:
def __init__(self, root: TreeNode):
self.tree = list()
queue = collections.deque()
queue.append(root)
while queue:
node = queue.popleft()
self.tree.append(node)
if node.left:
queue.append(node.left)
if node.right:
queue.append(node.right)
def insert(self, v: int) -> int:
_len = len(self.tree)
idx_parent_node = (_len-1)//2
parent_node = self.tree[idx_parent_node]
node = TreeNode(v)
if not parent_node.left:
parent_node.left = node
else:
parent_node.right = node
self.tree.append(node)
return parent_node.val
def get_root(self) -> TreeNode:
return self.tree[0]
# Your CBTInserter object will be instantiated and called as such:
# obj = CBTInserter(root)
# param_1 = obj.insert(v)
# param_2 = obj.get_root()并查集 (Union find)
并查集（Union-Find / disjoint set union）是解决动态连通性问题的一类非常高效的数据结构.
例子, 有一组数 Arr = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}. 进行find和union的操作:
执行 Union(2,1):
执行: Union(4,3) Union(8,4) Union(9,3)
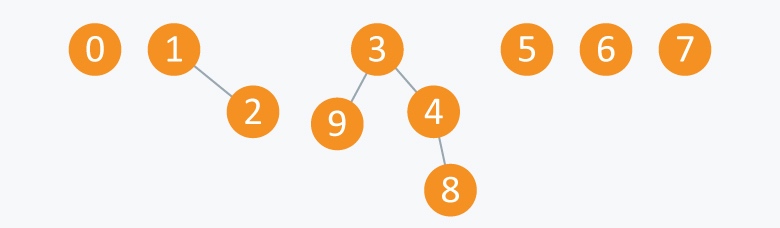
执行 Union(6,5)
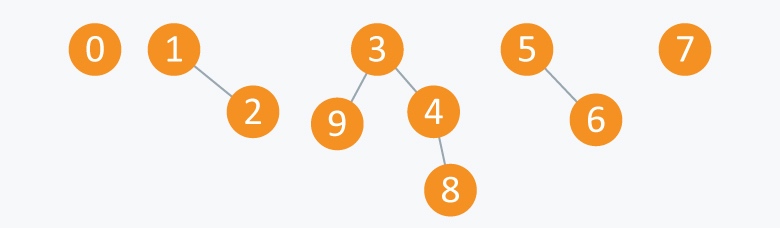
现在, 它有5个subset:
- {3,4,8,9}
- {1,2}
- {5,6}
- {0}
- {7}
如果要判断两个数是否连通,
- find(0,7) 会返回False
- find(8,9) 虽然他们不是直接连通, 但是他们在同一条路径上, 所以会返回True
通过数结构来提高效率, Arr={0,1,2,3,4,5}
执行Union(1,0), 将0设为根节点 root(0), 作为1的父节点.
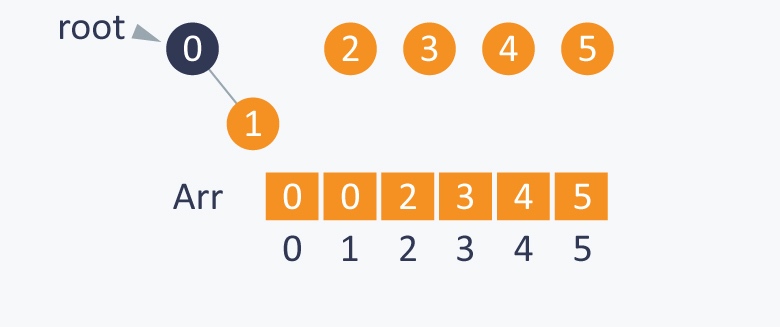
执行Union(0,2), 将2设为0的父节点, 2变成根节点 root(2)
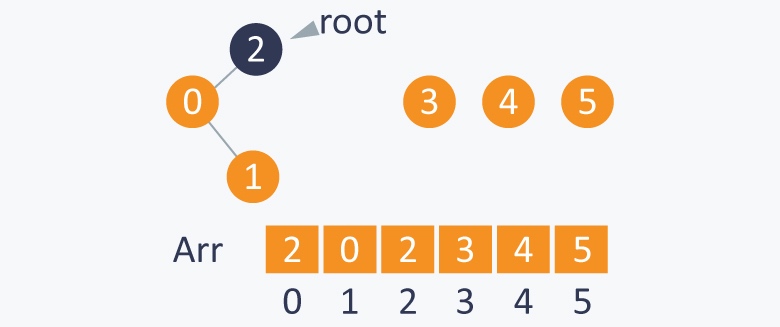
执行 Union (3, 4), 4变成3的的父节点, 4为根节点 root(4)
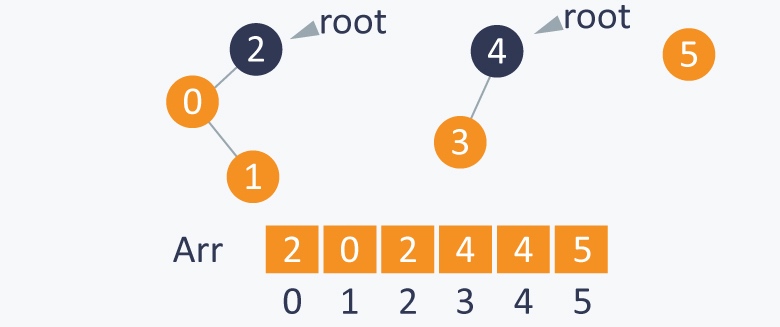
执行 Union(1,4), 将4变成跟节点 root(4), 由于1的跟节点为root(2), 所以4就变成了2的父节点
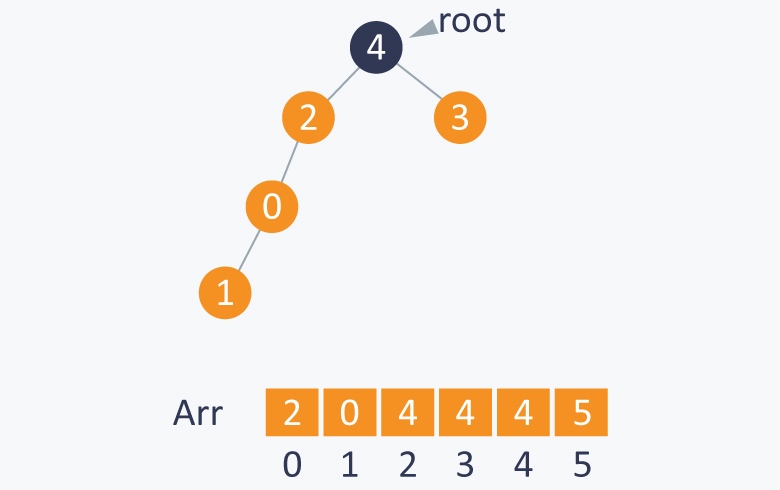
另一例子, 如果要union(1,5):
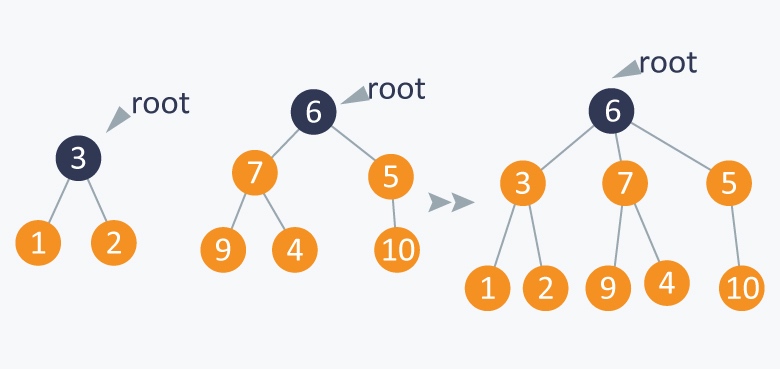
1的根节点为root(3), 5的根节点为root(6), 所以root(6)就变成了3的父节点.
总体上来说，这个数据结构就是在维护一个元素间有从属关系的数组，它有两个基本方法：
- find(x), 找到元素 x 的根节点，通常在 union find 维护的数组中，元素是作为索引的形式存在，索引对应的值是它父亲的索引；这个 find() 方法就是递归地寻找父亲，直到某个节点的父亲是自己，就返回这个节点
- union(x,y), 联合元素 x 和 元素 y，即把 x 和 y 所属的部分并起来，实现方法就是找到 x 和 y 各自的根节点，让其中一个根节点依附于另一个
code:
第一种方法, union(p,q)的时候只是单纯将数组的q位置上的数替换成p, 效率最低; 但是find(p)只需直接返回数组中p上的数, 效率高
class Quick_Find:
def __init__(self,N):
self.count = N
self.ids = [i for i in range(self.count)]
def connect(self,p,q):
return self.find(p) == self.find(q)
def find(self,p):
return self.ids[p]
def union(self,p,q):
pId = self.find(p)
qId = self.find(q)
if pId == qId:
return
for i in range(len(self.ids)):
if self.ids[i] == pId:
self.ids[i] = qId
self.count-=1
def getcount(self):
return self.count第二种方法, union(p,q)的时候直接将数组的q位置上的数替换成p, 效率最高; 但是find(p)需循环直到找到根节点, 效率低
class Quick_Union:
def __init__(self,N):
self.count = N
self.ids = [i for i in range(N)]
def connect(self,p,q):
return self.find(p) == self.find(q)
def find(self,p):
while self.ids[p] != p: # 循环，直到找到根节点
p = self.ids[p]
return p
def union(self,p,q):
pID = self.find(p)
qID = self.find(q)
if pID == qID:
return
self.ids[pID] = qID
self.count -= 1
def getcount(self):
return self.count第三种方法使用字典来储存:
f = {}
def find(x): # 为了找到联通的根节点
f.setdefault(x, x)
if f[x] != x:
f[x] = find(f[x])
return f[x]
def union(x, y):
f[find(y)] = find(x)
class Union_Find:
def __init__(self, N):
self.ids = [i for i in range(N)]
self.n = N
self.count = N
def find(self, x):
if x >= self.n:
return -1
if self.ids[x] != x:
return self.find(self.ids[x])
else:
return x
def union(self, x, y):
if x >= self.n or y >= self.n:
return False
root_x = self.find(x)
root_y = self.find(y)
if root_x != root_y:
self.ids[root_x] = root_y
self.count -= 1
return True
def connect(self,x,y):
return self.find(x) == self.find(y)
def getcount(self):
return self.countclass Weighted_Union_Find:
def __init__(self,N):
self.count = N
self.ids = [i for i in range(N)]
self.size = [1 for i in range(N)] # 加权
def connect(self,p,q):
return self.find(p) == self.find(q)
def find(self,p):
while self.ids[p] != p:
p = self.ids[p]
return p
def union(self,p,q):
pID = self.find(p)
qID = self.find(q)
if pID == qID:
return
if self.size[pID] < self.size[qID]: # 小的树并到大的树下
self.ids[pID] = qID
self.size[qID] += self.size[pID]
else:
self.ids[qID] = pID
self.size[pID] += self.size[qID]
self.count-=1
def getcount(self):
return self.count
'''
s = [0,1,2,3,4,5,6,7]
after union [2,3],[1,0],[0,4],[5,7],[6,2]:
4 -> 0 -> 1
3 -> 6 -> 2
7 -> 5
'''
if __name__ == '__main__':
# N,M = list(map(int,input().split())) # N为节点数目 M为输入关系系的数目
N = 8 # N为节点数目
s = [[2,3],[1,0],[0,4],[5,7],[6,2]]
# uf = Quick_Find(N)
# uf = Quick_Union(N)
uf = Weighted_Union_Find(N)
for p,q in s:
# p,q = list(map(int,input().split())) # p、q建立关系
if not uf.connect(p,q): # 若还未连接
uf.union(p,q)
print(uf.find(1)) # 4
print(uf.find(2)) # 3
print(uf.find(5)) # 7
print(uf.getcount()) # 3前缀树
前缀树 Trie, 又称 字典树.
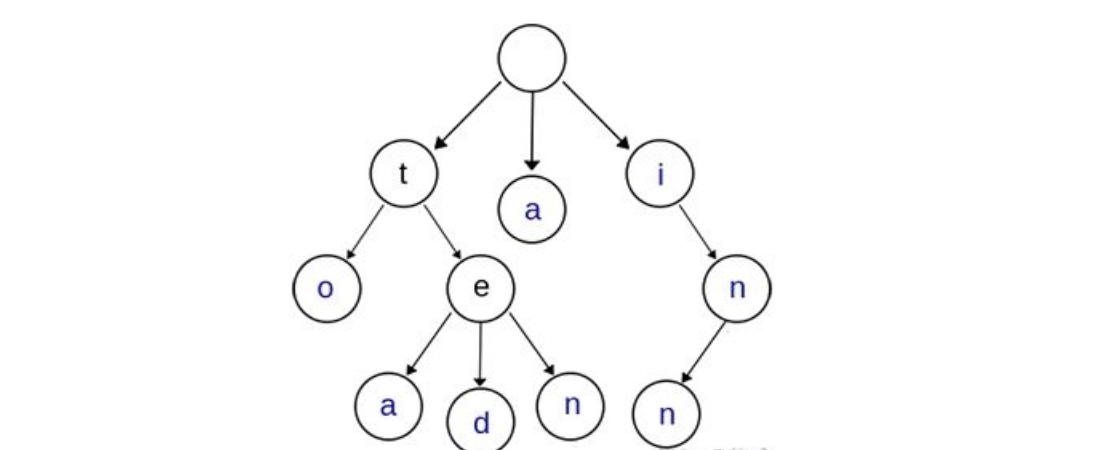从上图归纳出Trie树基本性质.
- 从根到某一个节点,拼接长字符串;
- 一个节点的子节点字符一定不相同
- Trie提高效率,用空间换时间
例子 - 实现一个 Trie (前缀树)，包含 insert, search, 和 startsWith 这三个操作:
Trie trie = new Trie();
trie.insert("apple");
trie.search("apple"); // 返回 true
trie.search("app"); // 返回 false
trie.startsWith("app"); // 返回 true
trie.insert("app");
trie.search("app"); // 返回 truecode:
要构建一个节点,节点递归下一个节点
from collections import defaultdict
class TrieNode:
def __init__(self):
self.children = defaultdict(TrieNode)
self.word = False
class Trie:
def __init__(self):
"""
Initialize your data structure here.
"""
self.root = TrieNode()
def insert(self, word):
"""
Inserts a word into the trie.
:type word: str
:rtype: void
"""
cur = self.root
for w in word:
cur = cur.children[w]
cur.word = True
def search(self, word):
"""
Returns if the word is in the trie.
:type word: str
:rtype: bool
"""
cur = self.root
for w in word:
if w not in cur.children:
return False
cur = cur.children[w]
if cur.word :
return True
return False
def startsWith(self, prefix):
"""
Returns if there is any word in the trie that starts with the given prefix.
:type prefix: str
:rtype: bool
"""
cur = self.root
for p in prefix:
if p not in cur.children:
return False
cur = cur.children[p]
return True
# Your Trie object will be instantiated and called as such:
# obj = Trie()
# obj.insert(word)
# param_2 = obj.search(word)
# param_3 = obj.startsWith(prefix)图遍历
图的表示方法
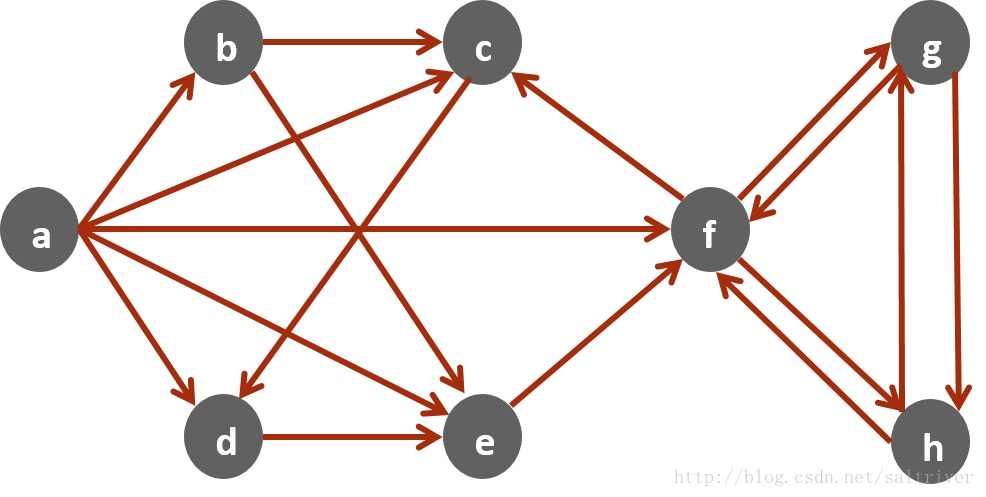
邻接表(adjacency list)
邻接表的核心思想就是针对每个顶点设置一个邻居表. 上图是一个有向图，分别有顶点a, b, c, d, e, f, g, h共8个顶点。使用邻接表就是针对这8个顶点分别构建邻居表，从而构成一个8个邻居表组成的结构，这个结构就是这个图的表示结构或者叫存储结构.
a, b, c, d, e, f, g, h = range(8)
N = [{b, c, d, e, f}, # a 的邻居表
{c, e}, # b 的邻居表
{d}, # c 的邻居表
{e}, # d 的邻居表
{f}, # e 的邻居表
{c, g, h}, # f 的邻居表
{f, h}, # g 的邻居表
{f, g}] # h 的邻居表这样，N构成了一个邻居节点集。可以通过N对图进行操作了
# 顶点f的邻居顶点
print(N[f]) # {2,6,7}
# 顶点g是否是a的邻居顶点
print(g in N[a]) # False
# 顶点a的邻居顶点个数
print(len(N[a])) # 5注意：每个顶点的邻居表都是一个集合(set) (因为不能重复存储邻居顶点). 在表示带权重值的图时，使用字典表示更合理.
N = [{b: 1, c: 2, d: 1, e: 2, f: 3}, # a 的邻居表
{c: 1, e: 2}, # b 的邻居表
{d: 3}, # c 的邻居表
{e: 1}, # d 的邻居表
{f: 2}, # e 的邻居表
{c: 1, g: 1, h: 1}, # f 的邻居表
{f: 1, h: 2}, # g 的邻居表
{f: 1, g: 2}] # h 的邻居表
# 边(a,f)的权重
if f in N[a]:
print(N[a][f]) # 3邻接矩阵(adjacency matrix)
邻接矩阵的核心思想是针对每个顶点设置一个表，这个表包含所有顶点，通过True/False来表示是否是邻居顶点。 还是针对上面的图，分别有顶点a, b, c, d, e, f, g, h共8个顶点。使用邻接矩阵就是针对这8个顶点构建一个8×8的矩阵组成的结构，这个结构就是我们这个图的表示结构或存储结构.
a, b, c, d, e, f, g, h = range(8)
N = [[0, 1, 1, 1, 1, 1, 0, 0], # a的邻接情况
[0, 0, 1, 0, 1, 0, 0, 0], # b 的邻居表
[0, 0, 0, 1, 0, 0, 0, 0], # c 的邻居表
[0, 0, 0, 0, 1, 0, 0, 0], # d 的邻居表
[0, 0, 0, 0, 0, 1, 0, 0], # e 的邻居表
[0, 0, 1, 0, 0, 0, 1, 1], # f 的邻居表
[0, 0, 0, 0, 0, 1, 0, 1], # g 的邻居表
[0, 0, 0, 0, 0, 1, 1, 0]] # h 的邻居表同样，可以对N进行图操作了，操作方式与邻接表方式有所不同
# 顶点g是否是a的邻居顶点
print(N[a][g]) # 0
# 顶点a的邻居顶点个数
print(sum(N[a])) # 5
# 顶点a的邻居顶点
neighbour = []
for i in range(len(N[f])):
if N[f][i]:
neighbour.append(i)
print(neighbour) # [2,6,7]在邻接矩阵表示法中，有一些非常实用的特性。
- 首先，可以看出，该矩阵是一个方阵，方阵的维度就是图中顶点的数量，同时还是一个对称矩阵，这样进行处理时非常方便。
- 其次，该矩阵对角线表示的是顶点与顶点自身的关系，一般图不允许出现自关联状态，即自己指向自己的边，那么对角线的元素全部为0；
- 最后，该表示方式可以不用改动即可表示带权值的图，直接将原来存储1的地方修改成相应的权值即可。当然， 0也是权值的一种，而邻接矩阵中0表示不存在这条边。出于实践中的考虑，可以对不存在的边的权值进行修改，将其设置为无穷大或非法的权值，如None，-99999/99999等
Dijkstra算法
Floyd-Warshall算法
Bellman-Ford算法
最小生成树
Kruskal算法
Prim算法
拓扑排序
在图论中，由一个有向无环图(Directed Acyclic Graph-DAG, 有向无环图一定存在拓扑排序)的顶点组成的序列，当且仅当满足下列条件时，称为该图的一个拓扑排序 (Topological sorting)
- 每个顶点出现且只出现一次
- 若A在序列中排在B的前面，则在图中不存在从B到A的路径
实际应用
- 检测编译时的循环依赖
- 制定有依赖关系的任务的执行顺序（例如课程表问题）
步骤：
- 选择一个入度为0的顶点并输出之；
- 从图中删除此顶点及其所有出边；
- 循环执行以上两步，直到不存在入度为0的顶点为止；如果剩下入度非0的顶点（输出的顶点数小于图中的顶点数），就说明有回路，不存在拓扑排序
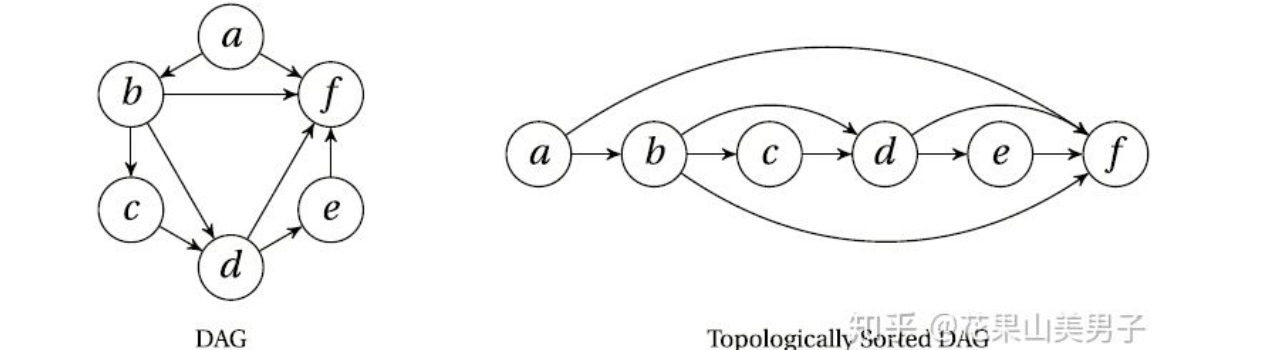
def topoSort(graph):
in_degrees = dict((u,0) for u in graph) #初始化所有顶点入度为0
vertex_num = len(in_degrees)
for u in graph:
for v in graph[u]:
in_degrees[v] += 1 #计算每个顶点的入度
print(in_degrees) # {'a': 0, 'b': 1, 'c': 1, 'd': 2, 'e': 1, 'f': 4}
Q = [u for u in in_degrees if in_degrees[u] == 0] # 筛选入度为0的顶点
print(Q) # ['a']
Seq = []
while Q:
u = Q.pop() #默认从最后一个删除
Seq.append(u)
for v in graph[u]:
in_degrees[v] -= 1 #移除其所有出边
if in_degrees[v] == 0:
Q.append(v) #再次筛选入度为0的顶点
print(in_degrees,'in while')
if len(Seq) == vertex_num: #输出的顶点数是否与图中的顶点数相等, 如果循环结束后存在非0入度的顶点说明图中有环，不存在拓扑排序
return Seq
else:
return None
G = {
'a':'bf',
'b':'cdf',
'c':'d',
'd':'ef',
'e':'f',
'f':''
}
print(topoSort(G))另一写法算法流程
- 统计所有点的入度，并初始化拓扑排序序列为空
- 将所有入度为0的点，放到如BFS初始的搜索队列中
- 将队列中的点一个一个释放出来，把访问其相邻的点，并把这些点的入度-1
- 如何发现某个点的入度为0时，则把这个点加入到队列中
- 当队列为空时，循环结束
入度(in-degree)是图论算法中重要的概念之一, 它通常指有向图中某点作为图中边的终点的次数之和.
def top_sort(graph):
node_to_indegree = self.get_indegree(graph)
# 初始化拓扑排序序列为空
order = []
start_nodes = [node for node in graph if node_to_indegree[node] == 0]
queue = collection.deque(start_nodes)
while queue:
head = queue.popleft()
order.append(node)
for neighbor in head.neighbors:
node_to_indegree[neighbor] -= 1
if node_to_indegree[neighbor] == 0:
queue.append(neighbor)
return order
def get_indegree(self, graph):
node_to_indegree = {x: 0 for x in graph}
for node in graph:
for neighbor in node.neighbors:
node_to_indegree[neighbor] += 1
return node_to_indegree查找子字符串，双指针模板
动态规划
https://charon.me/posts/leetcode/dp/
状态搜索
贪心
Buy & Sell stock
解题思路 受启发自精选题解 一个方法团灭 6 道股票问题 穷举，你有再多的状态，要做的就是一把梭全部列举出来。这个问题的「状态」有三个，第一个是天数，第二个是允许交易的最大次数，第三个是当前的持有状态（即之前说的 rest 的状态，我们不妨用 1 表示持有，0 表示没有持有）。然后我们用一个三维数组就可以装下这几种状态的全部组合：
dp[i][k][0 or 1]
0 <= i <= n-1, 1 <= k <= K
n 为天数，大 K 为最多交易数
dp[i][k][0] = max(dp[i-1][k][0], dp[i-1][k][1] + prices[i])
max( 选择 rest , 选择 sell )
解释：今天我没有持有股票，有两种可能：
要么是我昨天就没有持有，然后今天选择 rest，所以我今天还是没有持有；
要么是我昨天持有股票，但是今天我 sell 了，所以我今天没有持有股票了。
dp[i][k][1] = max(dp[i-1][k][1], dp[i-1][k-1][0] - prices[i])
max( 选择 rest , 选择 buy )
解释：今天我持有着股票，有两种可能：
要么我昨天就持有着股票，然后今天选择 rest，所以我今天还持有着股票；
要么我昨天本没有持有，但今天我选择 buy，所以今天我就持有股票了。dp[-1][k][0] = 0
解释：因为 i 是从 0 开始的，所以 i = -1 意味着还没有开始，这时候的利润当然是 0 。
dp[-1][k][1] = -infinity
解释：还没开始的时候，是不可能持有股票的，用负无穷表示这种不可能。
dp[i][0][0] = 0
解释：因为 k 是从 1 开始的，所以 k = 0 意味着根本不允许交易，这时候利润当然是 0 。
dp[i][0][1] = -infinity
解释：不允许交易的情况下，是不可能持有股票的，用负无穷表示这种不可能。把上面的状态转移方程总结一下：
base case：
dp[-1][k][0] = dp[i][0][0] = 0
dp[-1][k][1] = dp[i][0][1] = -infinity
状态转移方程：
dp[i][k][0] = max(dp[i-1][k][0], dp[i-1][k][1] + prices[i])
dp[i][k][1] = max(dp[i-1][k][1], dp[i-1][k-1][0] - prices[i])本题(309.含有冷冻期)因为不限制买卖次数, 所以k这个维度可以省去. 状态转移即变为
dp[i][0] = max(dp[i-1][0], dp[i-1][1]+prices[i-1])
dp[i][1] = max(dp[i-1][1], dp[i-2][0]-prices[i-1])代码L
class Solution:
def maxProfit(self, prices: List[int]) -> int:
if not prices: return 0
l = len(prices)
dp = [[0, 0] for _ in range(l+1)]
dp[0][1] = float('-inf')
dp[1][1] = -prices[0]
for i in range(2, l+1): # 因为下面有i-2所以从2开始, 自行去填0-1的base case
dp[i][0] = max(dp[i-1][0], dp[i-1][1]+prices[i-1])
dp[i][1] = max(dp[i-1][1], dp[i-2][0]-prices[i-1])
return dp[-1][0]