Dynamic Programming
Intro
动态规划就是将大问题拆分成小的子问题(最优子结构)
ref:
- MIT10题 https://people.cs.clemson.edu/~bcdean/dp_practice/
- 十大 https://zhuanlan.zhihu.com/p/107501014
- 刷题 https://leetcode-cn.com/tag/dynamic-programming/
- 40道 https://mp.weixin.qq.com/s/pg-IJ8rA1duIzt5hW1Cycw
- https://www.zhihu.com/question/39948290/answer/883302989
动态规划的三大步骤 动态规划,无非就是利用历史记录,来避免重复计算。而这些历史记录,需要一些变量来保存,一般是用一维数组或者二维数组来保存.
- 定义数组元素的含义. 会用一个数组,来保存历史数组,假设用一维数组 dp[], 重点是如何规定你这个数组元素的含义,例如 dp[i] 是代表什么意思?
- 找出数组元素之间的关系式(又叫状态转移的方程式). 当要计算 dp[n] 时,是可以利用 dp[n-1],dp[n-2]…..dp[1],来推出 dp[n] 的,也就是可以利用历史数据来推出新的元素值,所以要找出数组元素之间的关系式,例如 dp[n] = dp[n-1] + dp[n-2],这个就是他们的关系式了 (最难)
- 找出初始值. 例如 dp[n] = dp[n-1] + dp[n-2]一直推下去的话,会由 dp[3] = dp[2] + dp[1]. 而 dp[2] 和 dp[1] 是不能再分解的了,所以必须要能够直接获得 dp[2] 和 dp[1] 的值,而这就是所谓的初始值.
Example1 - 爬楼梯 (一维DP)
问题: > 一只青蛙一次可以跳上1级台阶,也可以跳上2级。求该青蛙跳上一个n级的台阶总共有多少种跳法
- 定义数组元素的含义
- 问题是要求青蛙跳上 n 级的台阶总共由多少种跳法,所以定义 dp[i] 的含义为:跳上一个 i 级的台阶总共有 dp[i] 种跳法. 这样, dp[n]就是要求的答案
- 找出数组元素间的关系式
- 要把一个规模比较大的问题分成几个规模比较小的问题,然后由小的问题推导出大的问题. 所以 dp[n] 的规模为 n,比它规模小的是 n-1, n-2, n-3…. 也就是说,dp[n] 一定会和 dp[n-1], dp[n-2]….存在某种关系的
- 对于这道题,由于情况可以选择跳一级,也可以选择跳两级,所以青蛙到达第 n 级的台阶有两种方式
- 一种是从第 n-1 级跳上来
- 一种是从第 n-2 级跳上来
- 由于要算所有可能的跳法的,所以有 dp[n] = dp[n-1] + dp[n-2]
- 找出初始条件
- 当 n = 1 时,dp[1] = dp[0] + dp[-1],而数组是不允许下标为负数的,所以对于 dp[1],必须要直接给出它的数值,相当于初始值 dp[1] = 1. 同样,dp[0] = 0.(因为 0 个台阶,那肯定是 0 种跳法了). 于是得出初始值:
- dp[0] = 0. dp[1] = 1. 即 n <= 1 时,dp[n] = n.
- 当 n = 2 时,dp[2] = dp[1] + dp[0] = 1 显然是错误的,应该是 dp[2] = 2
代码:
def stair(n):
if n < 2:
return n
dp = [0] * (n+1)
dp[0] = 0
dp[1] = 1
dp[2] = 2
for i in range(2,n+1):
dp[i] = dp[i-1] + dp[i-2]
print(dp)
return dp[-1]Example2 - 不同路径 (二维DP)
问题: > 一个机器人位于一个 m x n 网格的左上角 > 机器人每次只能向下或者向右移动一步. 机器人试图达到网格的右下角 > 问总共有多少条不同的路径?
- 定义数组元素的含义
- 由于目的是从左上角到右下角一共有多少种路径, 所以定义 dp[i][j]的含义为:当机器人从左上角走到(i, j) 这个位置时,一共有 dp[i][j] 种路径. 那么, dp[m-1] [n-1] 就是答案 (m,n分别是行数,列数)
- 找出关系数组元素间的关系式
- 由于机器人可以向下走或者向右走,所以有两种方式到达
- 一种是从 (i-1, j) 这个位置走一步到达
- 一种是从(i, j - 1) 这个位置走一步到达
- 因为是计算所有可能的步骤,所以是把所有可能走的路径都加起来,最终关系式是 dp[i][j] = dp[i-1][j] + dp[i][j-1]
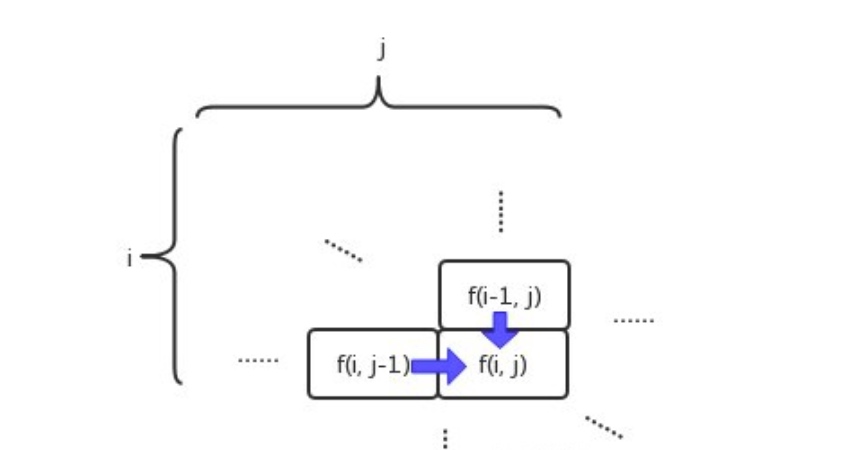
- 由于机器人可以向下走或者向右走,所以有两种方式到达
- 找出初始值
- 在 dp[i][j] 中, i 或者 j 不能为 0, 不然 i - 1 或者 j - 1 就变成负数了. 所以初始值是计算出所有的 dp[0][0…n-1] 和所有的 dp[0…m-1][0]. 相当于计算网格中的最上面一行和左边一列. 因此初始值如下:
- dp[0][0…n-1] = 1 ==> 相当于最上面一行,机器人只能一直往右走
- dp[0…m-1][0] = 1 ==> 相当于最左面一列,机器人只能一直往下走
- 在 dp[i][j] 中, i 或者 j 不能为 0, 不然 i - 1 或者 j - 1 就变成负数了. 所以初始值是计算出所有的 dp[0][0…n-1] 和所有的 dp[0…m-1][0]. 相当于计算网格中的最上面一行和左边一列. 因此初始值如下:
代码:
def countPath(m,n):
dp = [[1]*n]*m # 节省空间, 只有 O(n) 的空间复杂度
# dp = [[1 for _ in range(n)] for _ in range(m)] # O(nm) 的空间复杂度
for i in range(1,m):
for j in range(1,n):
dp[i][j] = dp[i-1][j] + dp[i][j-1]
return dp[m-1][n-1]
Example3 - 不同路径 (二维DP)
问题: > 给定一个包含非负整数的 m x n 网格,请找出一条从左上角到右下角的路径,使得路径上的数字总和为最小 (每次只能向下或者向右移动一步)
输入:
arr = [
[1,3,1],
[1,5,1],
[4,2,1]
]
输出: 7
解释: 因为路径 1→3→1→1→1 的总和最小- 定义数组元素的含义
- 和上题一样, 定义 dp[i][j]的含义为:当从左上角走到(i, j) 这个位置时,最小的路径和是 dp[i][j]
- 找出关系数组元素间的关系式
- 和上题类似
- 一种是从 (i-1, j) 这个位置走一步到达
- 一种是从(i, j - 1) 这个位置走一步到达
- 不过这次不是计算所有可能路径,而是计算哪一个路径和是最小的,那么要从这两种方式中选择一种,使得dp[i][j] 的值是最小的,所以:
- dp[i][j] = min(dp[i-1][j], dp[i][j-1]) + arr[i][j]
- arr[i][j] 表示当前网格的值
- dp[i][j] = min(dp[i-1][j], dp[i][j-1]) + arr[i][j]
- 和上题类似
- 找出初始值
- 初始值如下:
- dp[0][j] = arr[0][j] + dp[0][j-1] ==> 最上一行的值(从左到右)不断累加
- dp[i][0] = arr[i][0] + dp[i][0] ==> 最左一列的值(从上到下)不断累加
- 初始值如下:
代码
def uniquePath(arr):
m = len(arr)
n = len(arr[0])
for i in range(1,m):
arr[i][0] += arr[i-1][0]
for j in range(1,n):
arr[0][j] += arr[0][j-1]
for i in range(1,m):
for j in range(1,n):
arr[i][j] = min(arr[i-1][j], arr[i][j-1]) + arr[i][j]
return arr[m-1][n-1]Example3 - 编辑距离 (二维DP)
问题: > 给定两个单词 word1 和 word2,计算出将 word1 转换成 word2 所使用的最少操作数. 可以对一个单词进行如下三种操作:插入一个字符 删除一个字符 替换一个字符
示例:
输入: word1 = "horse", word2 = "ros"
输出: 3
解释:
horse -> rorse (将 'h' 替换为 'r')
rorse -> rose (删除 'r')
rose -> ros (删除 'e'):- 定义数组元素的含义
- 目的求将 word1 转换成 word2 所使用的最少操作数. 所以定义 dp[i][j]的含义为:当字符串 word1 的长度为 i,字符串 word2 的长度为 j 时,将 word1 转化为 word2 所使用的最少操作次数为 dp[i][j]
- 找出关系数组元素间的关系式
- 大部分情况下,dp[i][j], dp[i-1][j], dp[i][j-1] 和 dp[i-1][j-1] 肯定存在某种关系
- 可以对 word1 进行三种操作 - 插入一个字符 删除一个字符 替换一个字符. 由于是要让操作的次数最小,所以要寻找最佳操作. 那么有如下关系式:
- 如果 word1[i] 与 word2[j] 相等,这个时候不需要进行任何操作,显然有 dp[i][j] = dp[i-1]j-1
- 如果 word1[i] 与 word2[j] 不相等,这个时候就必须进行调整,而调整的操作有 3 种,要选择一种. 三种操作对应的关系试如下(注意字符串与字符的区别):
- 如果把字符 word1[i] 替换成与 word2[j] 相等,则有 dp[i][j] = dp[i-1][j-1] + 1
- 如果在字符串 word1末尾插入一个与 word2[j] 相等的字符,则有 dp[i][j] = dp[i][j-1] + 1
- 如果把字符 word1[i] 删除,则有 dp[i][j] = dp[i-1][j] + 1
- 应该选择一种操作,使得 dp[i][j] 的值最小, 所以:
- dp[i][j] = min(dp[i-1][j-1],dp[i][j-1],dp[i-1][j]) + 1
- 找出初始值
- 初始值是计算出所有的 dp[0][0…n] 和所有的 dp[0…m][0]. 因为当有一个字符串的长度为 0 时,转化为另外一个字符串,那就只能一直进行插入或者删除操作了
代码
def minDistance(word1, word2):
n1 = len(word1)
n2 = len(word2)
dp = [[1]*n1]*n2
for i in range(1,n1):
for j in range(1,n2):
if word1[i-1] == word2[j-1]:
dp[i][j] = dp[i-1][j-1]
else:
dp[i][j] = min(dp[i-1][j], dp[i][j-1], dp[i-1][j-1]) + 1
return dp[n1-1][n2-1]Example3 - 编辑距离 (二维DP)
问题: > 给定不同面额的硬币 coins 和一个总金额 amount。编写一个函数来计算可以凑成总金额所需的最少的硬币个数。如果没有任何一种硬币组合能组成总金额,返回 -1
输入: coins = [1, 2, 5], amount = 11
输出: 3
解释: 11 = 5 + 5 + 1- 定义数组元素的含义
- 目的求凑成amount所需coins的最少个数. 所以定义 dp[i]的含义为:amount i所需的最少coins的个数为 dp[i]
- 找出关系数组元素间的关系式
- 使得dp[i]的值是最小的关系: min(dp[i], dp[i-coin]+1)
- 找出初始值
- 初始一个amount 长度的数组, 所有值都为无限大.
代码
coins = [1,2,5]
amount = 11
def coinChange(coins: List[int], amount: int) -> int:
dp=[float("inf")]*(amount+1)
dp[0]=0
for i in range(1,amount+1):
for coin in coins:
if i>=coin:
dp[i]=min(dp[i],dp[i-coin]+1)
return dp[-1] if(dp[-1]!=float("inf")) else -11. Maximum Value Contiguous Subsequence
最大子序和
Given a sequence of n real numbers A(1) … A(n), determine a contiguous subsequence A(i) … A(j) for which the sum of elements in the subsequence is maximized.
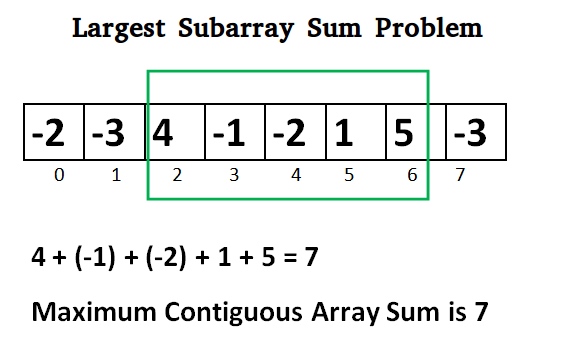
子问题: M(j): max sum over all windows ending at j
nums = [-2, -3, 4, -1, -2, 1, 5, -3]
res = [nums[0]]
for i in range(1,len(nums)):
res.append(max(res[i-1]+nums[i],nums[i]))
print(res) # [0, 1, 1, 2, 2, 1, 2, 2, 3, 3, 2]
print(max(res)) # 72. Making Change
零钱兑换
You are given n types of coin denominations(硬币面额) of values v(1) < v(2) < … < v(n) (all integers). Assume v(1) = 1, so you can always make change for any amount of money C. Give an algorithm which makes change for an amount of money C with as few coins as possible.
子问题: M(j): minimum # coins required to make change for amount of money j
changes = [1,2,5]
amount = 10
res = [10000] * (amount+1)
res[0] = 0
print(res)
for i in range(1,amount+1):
for j in changes:
if i-j > -1:
res[i] = (min(res[i],res[i-j]+1))
print(res[amount]) # 2
print(res) #[0, 1, 1, 2, 2, 1, 2, 2, 3, 3, 2]i - j means amount minus changes, ‘res[i-j]’ means residual money can be found in the previous ‘res’
3. Longest Increasing Subsequence
最长上升子序列
Given a sequence of n real numbers A(1) … A(n), determine a subsequence (not necessarily contiguous) of maximum length in which the values in the subsequence form a strictly increasing sequence.

子问题: L(j): longest strictly increasing subsequence ending at position j
L(i) = 1 + max( L(j) ) where 0 < j < i and arr[j] < arr[i]; or L(i) = 1, if no such j exists.
arr = [10, 22, 9, 33, 21, 50, 41, 60, 80]
lis = [1] * len(arr)
for i in range(1,len(arr)):
for j in range(i):
if arr[i] > arr[j]:
lis[i] = max(lis[i], lis[j] + 1)
print(lis) # [1, 2, 1, 3, 2, 4, 4, 5, 6]
print(max(lis)) # 64. Box Stacking
https://www.geeksforgeeks.org/box-stacking-problem-dp-22/
You are given a set of n types of rectangular 3-D boxes, where the i^th box has height h(i), width w(i) and depth d(i) (all real numbers). You want to create a stack of boxes which is as tall as possible, but you can only stack a box on top of another box if the dimensions of the 2-D base of the lower box are each strictly larger than those of the 2-D base of the higher box.(The stack should be such that any box should have its based dimensions strictly smaller than the box below. i.e. both length and breadth). Of course, you can rotate a box so that any side functions as its base. It is also allowable to use multiple instances of the same type of box.
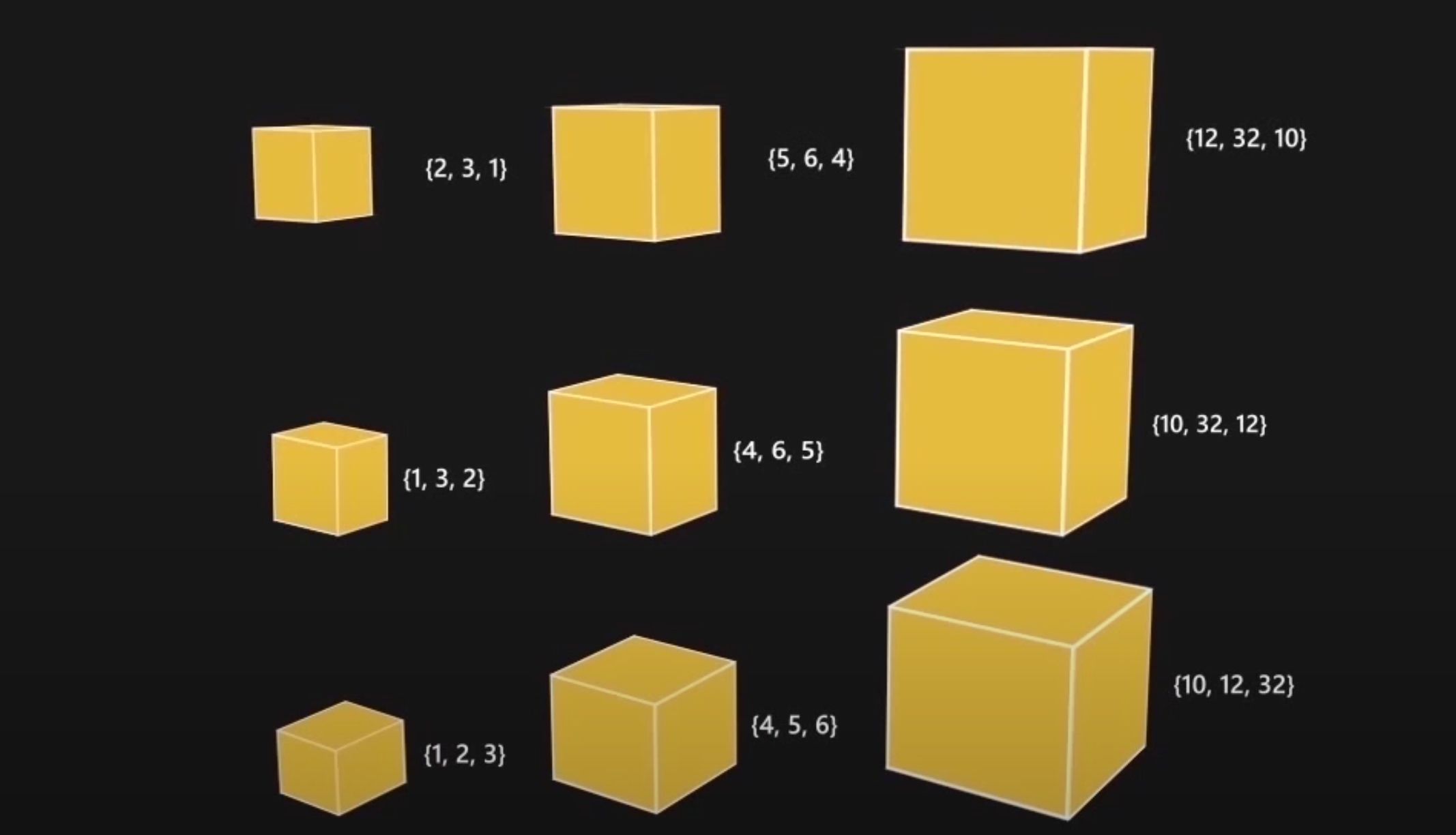
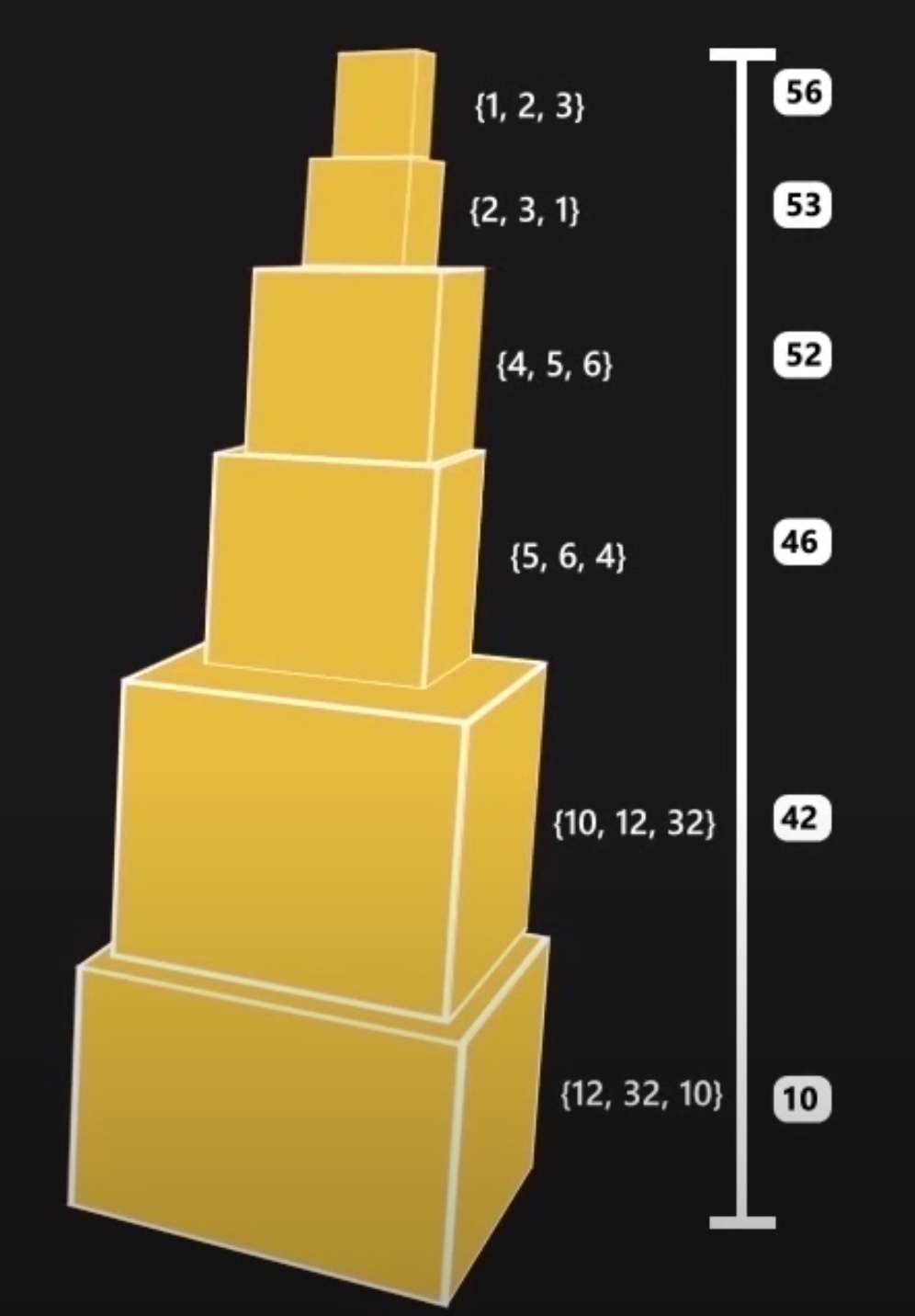
Note: A variation of Longest Increasing Subsequence problem
- n个类型的长方体(box),第i个长方体表示为:长为d[i],宽为w[i],高为h[i],(宽w[i] <= 长d[i])
- 一个box j可以放在box i上面,w[j]<w[i] && d[j] <d[i]
- box可以旋转,长、宽、高随着变化
- 每种类型的box使用次数不限
怎么摞这些box(按什么顺序从下往上放置这些box),使它的高度最高
class Box: # Representation of a box def __init__(self, h, w, d): self.h = h self.w = w self.d = d def __lt__(self, other): return self.d * self.w < other.d * other.w def maxStackHeight(arr, n): # Create an array of all rotations of given boxes. # For example, for a box {1, 2, 3}, consider three instances: # {{1, 2, 3}, {2, 1, 3}, {3, 1, 2}} rot = [Box(0, 0, 0) for _ in range(3 * n)] index = 0 for i in range(n): # Copy the original box rot[index].h = arr[i].h rot[index].d = max(arr[i].d, arr[i].w) rot[index].w = min(arr[i].d, arr[i].w) index += 1 # First rotation of the box rot[index].h = arr[i].w rot[index].d = max(arr[i].h, arr[i].d) rot[index].w = min(arr[i].h, arr[i].d) index += 1 # Second rotation of the box rot[index].h = arr[i].d rot[index].d = max(arr[i].h, arr[i].w) rot[index].w = min(arr[i].h, arr[i].w) index += 1 # Now the number of boxes is 3 * n n *= 3 # Sort the array 'rot[]' in non-increasing order of base area rot.sort(reverse = True) # for i in range(n): # print(rot[i].h, 'x', rot[i].w, 'x', rot[i].d) # printall rotations # Initialize msh values for all indexes # msh[i] --> is Maximum possible Stack Height with box i on top msh = [0] * n for i in range(n): msh[i] = rot[i].h # Compute optimized msh values in bottom up manner for i in range(1, n): for j in range(0, i): if (rot[i].w < rot[j].w and rot[i].d < rot[j].d): if msh[i] < msh[j] + rot[i].h: msh[i] = msh[j] + rot[i].h maxm = -1 for i in range(n): maxm = max(maxm, msh[i]) return maxm # Driver Code if __name__ == "__main__": arr = [Box(1, 2, 3), Box(4, 5, 6), Box(10, 12, 32)] # Box(4, 6, 7) n = len(arr) print("The maximum possible height of stack is", maxStackHeight(arr, n))
https://www.geeksforgeeks.org/box-stacking-problem-dp-22/?ref=lbp
5. Building Bridges
Consider a 2-D map with a horizontal river passing through its center. There are n cities on the southern bank with x-coordinates a(1) … a(n) and n cities on the northern bank with x-coordinates b(1) … b(n). You want to connect as many north-south pairs of cities as possible with bridges such that no two bridges cross. When connecting cities, you can only connect city i on the northern bank to city i on the southern bank.
8 1 4 3 5 2 6 7
<---- Cities on the other bank of river---->
--------------------------------------------
<--------------- River--------------->
--------------------------------------------
1 2 3 4 5 6 7 8
<------- Cities on one bank of river------->Example:
Input : 6 4 2 1
2 3 6 5
Output : Maximum number of bridges = 2
Explanation: Let the north-south x-coordinates
be written in increasing order.
1 2 3 4 5 6
\ \
\ \ For the north-south pairs
\ \ (2, 6) and (1, 5)
\ \ the bridges can be built.
\ \ We can consider other pairs also,
\ \ but then only one bridge can be built
\ \ because more than one bridge built will
\ \ then cross each other.
\ \
1 2 3 4 5 6
Input : 8 1 4 3 5 2 6 7
1 2 3 4 5 6 7 8
Output : Maximum number of bridges = 5def buildingBridges(coord):
sortNorth = sorted(coord)
# find longest increasing subsequence in south coord
memo = [1]*len(sortNorth)
#print(sortNorth)
for i in range(len(sortNorth)):
maxSub = 0
for j in range(i):
if sortNorth[i][1] > sortNorth[j][1]:
maxSub = max(maxSub, memo[j])
memo[i] = maxSub + 1
# print(max(memo))
return max(memo)
res = buildingBridges([[8,1],[1,2],[4,3],[3,4],[5,5],[2,6],[6,7],[7,8]])
#coord = [[north1, south1],[north2, south2],...]
print(res) # 10Time Complexity: O(n^2)
https://www.geeksforgeeks.org/dynamic-programming-building-bridges/
6. Integer Knapsack Problem
Given weights and values of n items, put these items in a knapsack of capacity W to get the maximum total value in the knapsack. In other words, given two integer arrays val[0..n-1] and wt[0..n-1] which represent values and weights associated with n items respectively. Also given an integer W which represents knapsack capacity, find out the maximum value subset of val[] such that sum of the weights of this subset is smaller than or equal to W. You cannot break an item, either pick the complete item, or don’t pick it (0-1 property).


Balanced Partition.
You have a set of n integers each in the range 0 … K. Partition these integers into two subsets such that you minimize |S1 - S2|, where S1 and S2 denote the sums of the elements in each of the two subsets.
Edit Distance.
Given two text strings A of length n and B of length m, you want to transform A into B with a minimum number of operations of the following types: delete a character from A, insert a character into A, or change some character in A into a new character. The minimal number of such operations required to transform A into B is called the edit distance between A and B.
Counting Boolean Parenthesizations.
You are given a boolean expression consisting of a string of the symbols ‘true’, ‘false’, ‘and’, ‘or’, and ‘xor’. Count the number of ways to parenthesize the expression such that it will evaluate to true. For example, there are 2 ways to parenthesize ‘true and false xor true’ such that it evaluates to true.
Optimal Strategy for a Game.
Consider a row of n coins of values v(1) … v(n), where n is even. We play a game against an opponent by alternating turns. In each turn, a player selects either the first or last coin from the row, removes it from the row permanently, and receives the value of the coin. Determine the maximum possible amount of money we can definitely win if we move first.
Leetcode
70. Climbing Stairs
Topic: Dynamic Programming
You are climbing a stair case. It takes n steps to reach to the top.
Each time you can either climb 1 or 2 steps. In how many distinct ways can you climb to the top?
Note: Given n will be a positive integer.
Example 1:
Input: 2
Output: 2
Explanation: There are two ways to climb to the top.
1. 1 step + 1 step
2. 2 stepsExample 2:
Input: 3
Output: 3
Explanation: There are three ways to climb to the top.
1. 1 step + 1 step + 1 step
2. 1 step + 2 steps
3. 2 steps + 1 stepn=1时, 有一种, n=2时, 有两种方法 n=3时, 有3种方法, 等于 n=1 和 n=2的方法数相加. 以此类推
Approach1
DP: As we can see this problem can be broken into subproblems, and it contains the optimal substructure property i.e. its optimal solution can be constructed efficiently from optimal solutions of its subproblems, we can use dynamic programming to solve this problem.
One can reach $i^{th}$step in one of the two ways:
- Taking a single step from
$(i-1)^{th}$step. - Taking a step of 2 from
$(i-2)^{th}$step.
So, the total number of ways to reach $i^{th}$ is equal to sum of ways of reaching $(i-1)^{th}$ step and ways of reaching $(i-2)^{th}$step.
Let $dp[i]$ denotes the number of ways to reach on $i^{th}$step:
$dp[i]=dp[i-1]+dp[i-2]$
def climbStairs(self, n: int) -> int:
temp = []
temp.append(1)
temp.append(2)
for i in range(2,n):
temp.append(temp[i-2] + temp[i-1])
return temp[n-1]Complexity Analysis
Time complexity : $O(n)$. Single loop upto n.
Space complexity : $O(n)$. dp array of size n is used.
Approach2
In the above approach we have used dp array where $dp[i]=dp[i-1]+dp[i-2]$. It can be easily analysed that $dp[i]$is nothing but $i^{th}$fibonacci number.
$Fib(n)=Fib(n-1)+Fib(n-2)$
Now we just have to find $n^{th}$number of the fibonacci series having 1 and 2 their first and second term respectively, i.e. $Fib(1)=1$ and $Fib(2)=2$
def climbStairs(self, n):
a, b = 1, 1
for i in range(n):
a, b = b, a + b
return aComplexity Analysis
Time complexity : $O(n)$. Single loop upto nn is required to calculate $n^{th}$fibonacci number.
Space complexity : $O(1)$. Constant space is used.
121. Best Time to Buy and Sell Stock
Topic: Array, Dynamic Programming
Say you have an array for which the ith element is the price of a given stock on day i.
If you were only permitted to complete at most one transaction (i.e., buy one and sell one share of the stock), design an algorithm to find the maximum profit.
Note that you cannot sell a stock before you buy one.
Example1:
Input: [7,1,5,3,6,4]
Output: 5
Explanation: Buy on day 2 (price = 1) and sell on day 5 (price = 6), profit = 6-1 = 5.
Not 7-1 = 6, as selling price needs to be larger than buying price.Example2:
Input: [7,6,4,3,1]
Output: 0
Explanation: In this case, no transaction is done, i.e. max profit = 0.Code:
def maxProfit(prices: List[int]) -> int:
n = len(prices)
if n == 0: return 0 # 边界条件
dp = [0] * n
minprice = prices[0]
for i in range(1, n):
minprice = min(minprice, prices[i])
dp[i] = max(dp[i - 1], prices[i] - minprice)
return dp[-1]时间复杂度:$\mathcal{O}(n)$
空间复杂度:$\mathcal{O}(n)$