LeetCode day8

5 minutes read
LeetCode
#LeetCode
views 962 words

189. Rotate Array

Topic: Array

Given an array, rotate the array to the right by k steps, where k is non-negative.

Follow up:

  • Try to come up as many solutions as you can, there are at least 3 different ways to solve this problem.
  • Could you do it in-place with O(1) extra space?  

Example 1:

Input: nums = [1,2,3,4,5,6,7], k = 3
Output: [5,6,7,1,2,3,4]
Explanation:
rotate 1 steps to the right: [7,1,2,3,4,5,6]
rotate 2 steps to the right: [6,7,1,2,3,4,5]
rotate 3 steps to the right: [5,6,7,1,2,3,4]

Example 2:

Input: nums = [-1,-100,3,99], k = 2
Output: [3,99,-1,-100]
Explanation: 
rotate 1 steps to the right: [99,-1,-100,3]
rotate 2 steps to the right: [3,99,-1,-100]

Constraints:

  • 1 <= nums.length <= 2 * 10^4
  • It’s guaranteed that nums[i] fits in a 32 bit-signed integer.
  • k >= 0

Approach1

my

def rotate(nums: List[int], k: int) -> None:
    """
    Do not return anything, modify nums in-place instead.
    """
    nums1 = nums[len(nums)-k:]
    nums2 = nums[:len(nums)-k]
    nums[:] = nums1+nums2
    
    # Below is same but faster
    # lenth = len(nums)
    # nums[:] = nums[lenth-k:]+nums[:lenth-k]

Approach2

当 k % len(nums) == 0 意味着数组的旋转结果还是常态，没有意义返回

否则交换数据要旋转的数据即可，eg： a, b = b, a 无需申请第三个变量

def rotate(nums: List[int], k: int) -> None:
    """
    Do not return anything, modify nums in-place instead.
    """
    k = k % len(nums)
    if k == 0:
        return
    nums[:-k], nums[-k:] = nums[-k:], nums[:-k]
    return

190. Reverse Bits

Topic: Bit manipulation

Reverse bits of a given 32 bits unsigned integer.

Example 1:

Input: 00000010100101000001111010011100
Output: 00111001011110000010100101000000
Explanation: The input binary string 00000010100101000001111010011100 represents the unsigned integer 43261596, so return 964176192 which its binary representation is 00111001011110000010100101000000.

Example 2:

Input: 11111111111111111111111111111101
Output: 10111111111111111111111111111111
Explanation: The input binary string 11111111111111111111111111111101 represents the unsigned integer 4294967293, so return 3221225471 which its binary representation is 10111111111111111111111111111111.

Note:

  • Note that in some languages such as Java, there is no unsigned integer type. In this case, both input and output will be given as signed integer type and should not affect your implementation, as the internal binary representation of the integer is the same whether it is signed or unsigned.
  • In Java, the compiler represents the signed integers using 2’s complement notation. Therefore, in Example 2 above the input represents the signed integer -3 and the output represents the signed integer -1073741825.  

Follow up:

  • If this function is called many times, how would you optimize it?

Approach1

每次填入一位数 (哈哈哈实在不懂bit manipulation)

def reverseBits( n: int) -> int:
    res = 0
    for i in range(32):
        res <<= 1
        res += n&1
        n >>= 1
    return res

Approach2

bin() 返回一个整数 int 或者长整数 long int 的二进制表示

zfill() 方法返回指定长度的字符串，原字符串右对齐，前面填充0

def reverseBits(self, n: int) -> int:
        # n: 00000010100101000001111010011100
        print(bin(n))
        print(bin(n)[2:])
        print(bin(n)[2:].zfill(32)[::-1])
        '''
        0b10100101000001111010011100
        10100101000001111010011100
        00111001011110000010100101000000
        '''
    return int(bin(n)[2:].zfill(32)[::-1], 2)

191. Number of 1 Bits

Topic: Bit manipulation

Write a function that takes an unsigned integer and return the number of ‘1’ bits it has (also known as the Hamming weight).

Example 1:

Input: 00000000000000000000000000001011
Output: 3
Explanation: The input binary string 00000000000000000000000000001011 has a total of three '1' bits.

Example 2:

Input: 00000000000000000000000010000000
Output: 1
Explanation: The input binary string 00000000000000000000000010000000 has a total of one '1' bit.

Example 3:

Input: 11111111111111111111111111111101
Output: 31
Explanation: The input binary string 11111111111111111111111111111101 has a total of thirty one '1' bits.

Note:

  • Note that in some languages such as Java, there is no unsigned integer type. In this case, the input will be given as signed integer type and should not affect your implementation, as the internal binary representation of the integer is the same whether it is signed or unsigned.
  • In Java, the compiler represents the signed integers using 2’s complement notation. Therefore, in Example 3 above the input represents the signed integer -3.  

Follow up:

  • If this function is called many times, how would you optimize it?

Approach1

my

def hammingWeight(n: int) -> int:
    tmp = bin(n)[2:]
    cnt = 0
    for i in tmp:
        # print(i,type(i))  # 1 <class 'str'>
        if i == '1':
            cnt+=1
    return cnt

Approach2

def hammingWeight(self, n: int) -> int:
        return bin(n).count('1')

198. House Robber

Topic: DP

You are a professional robber planning to rob houses along a street. Each house has a certain amount of money stashed, the only constraint stopping you from robbing each of them is that adjacent houses have security system connected and it will automatically contact the police if two adjacent houses were broken into on the same night.

Given a list of non-negative integers representing the amount of money of each house, determine the maximum amount of money you can rob tonight without alerting the police.

Example 1:

Input: [1,2,3,1]
Output: 4
Explanation: Rob house 1 (money = 1) and then rob house 3 (money = 3).
             Total amount you can rob = 1 + 3 = 4.

Example 2:

Input: [2,7,9,3,1]
Output: 12
Explanation: Rob house 1 (money = 2), rob house 3 (money = 9) and rob house 5 (money = 1).
             Total amount you can rob = 2 + 9 + 1 = 12.
  1. 定义子问题
  2. 写出子问题的递推关系 (key step)
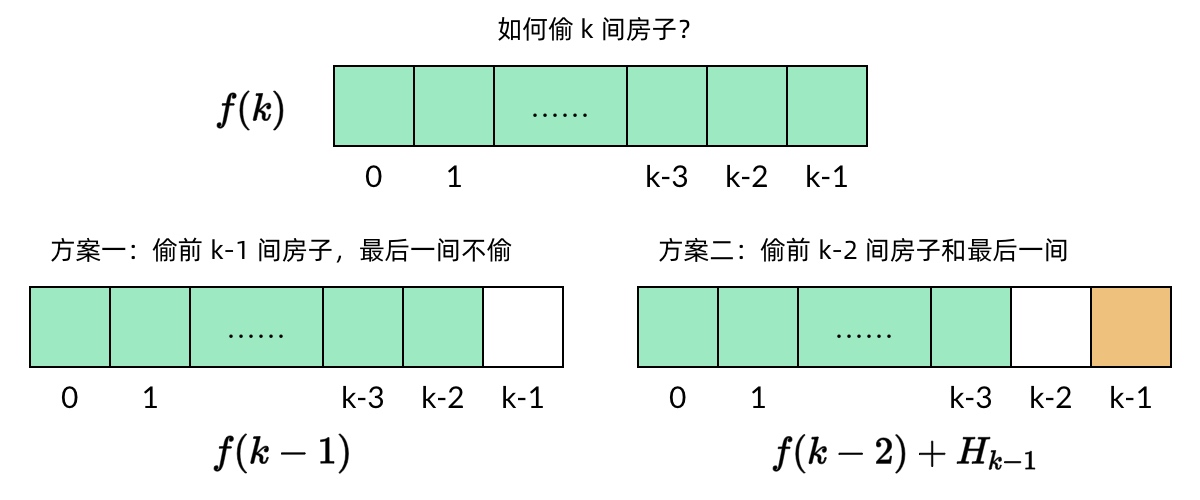
    • $f(k)=max\{f(k−1), H_{k−1} + f(k−2)\}$
      • 当 k=0 时，没有房子，所以 $f(0) = 0$
      • 当 k=1 时，只有一个房子，偷这个房子即可，所以 $f(1) = H_0$
  3. 确定 DP 数组的计算顺序 (自底向上的,使用 dp 数组的循环方法)
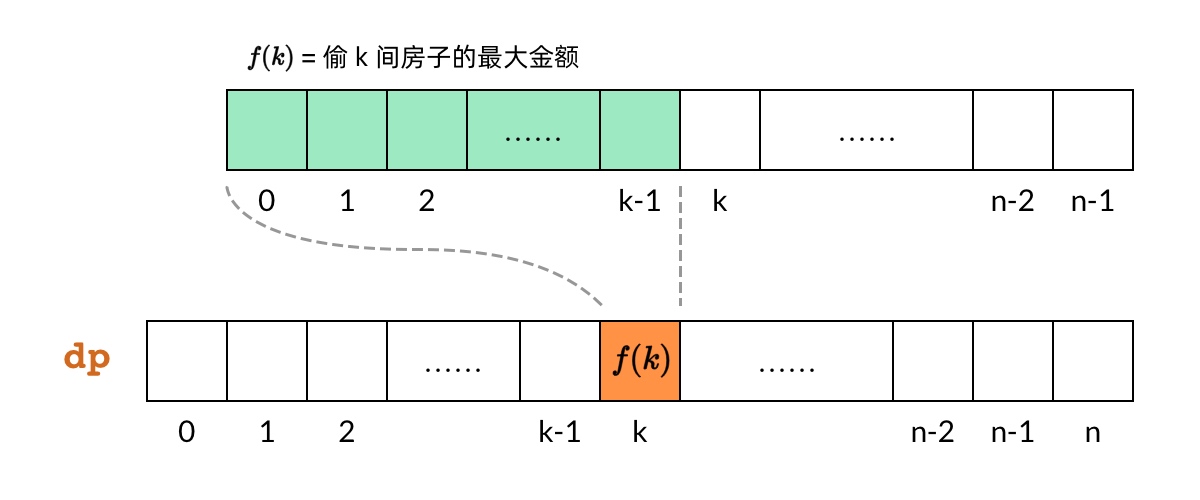    • dp[k] 对应子问题 f(k)，即偷前 k 间房子的最大金额
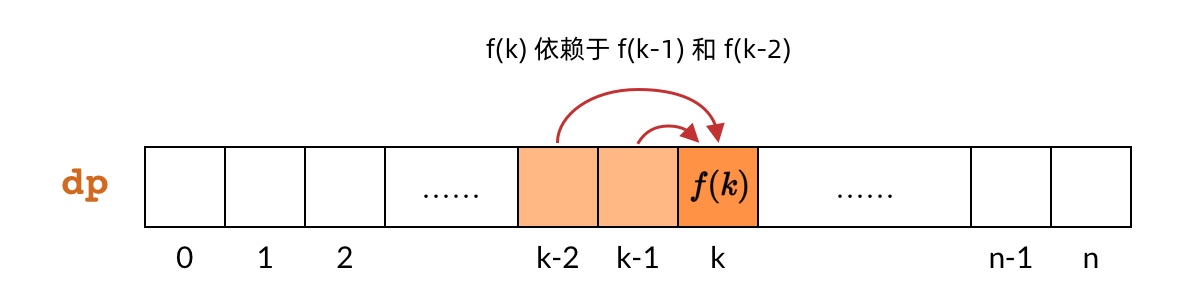    • dp[k] 依赖 dp[k-1] 和 dp[k-2]

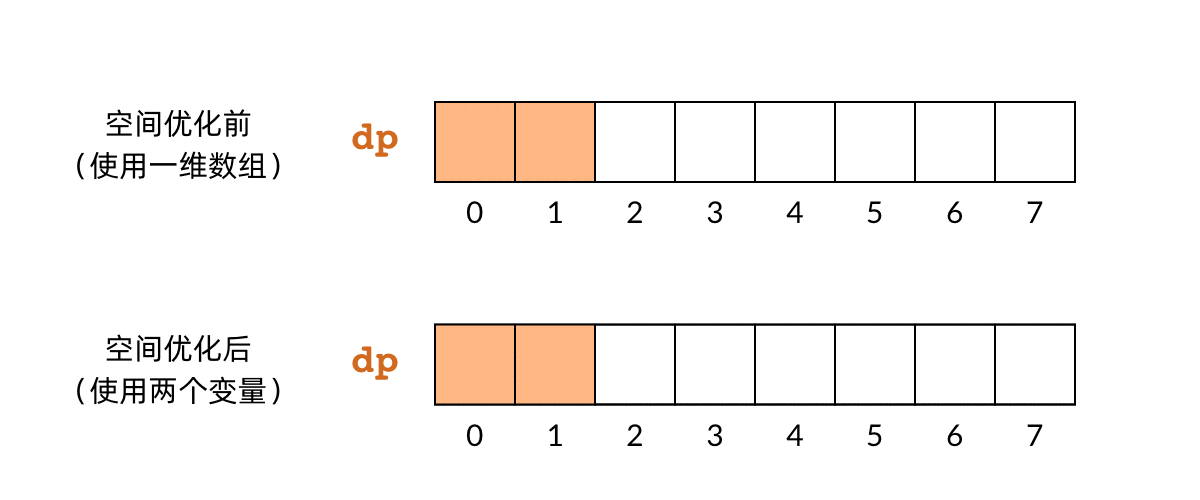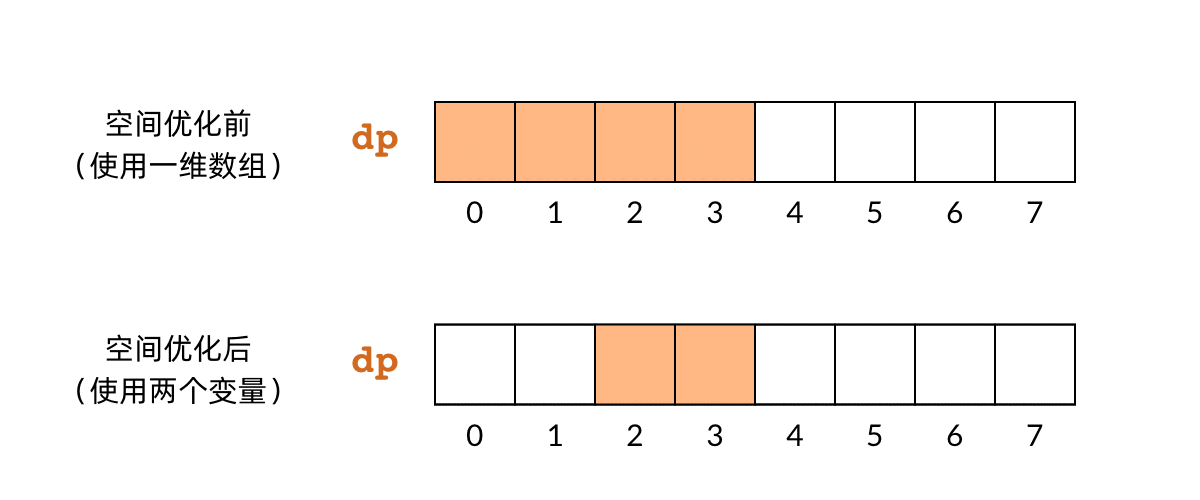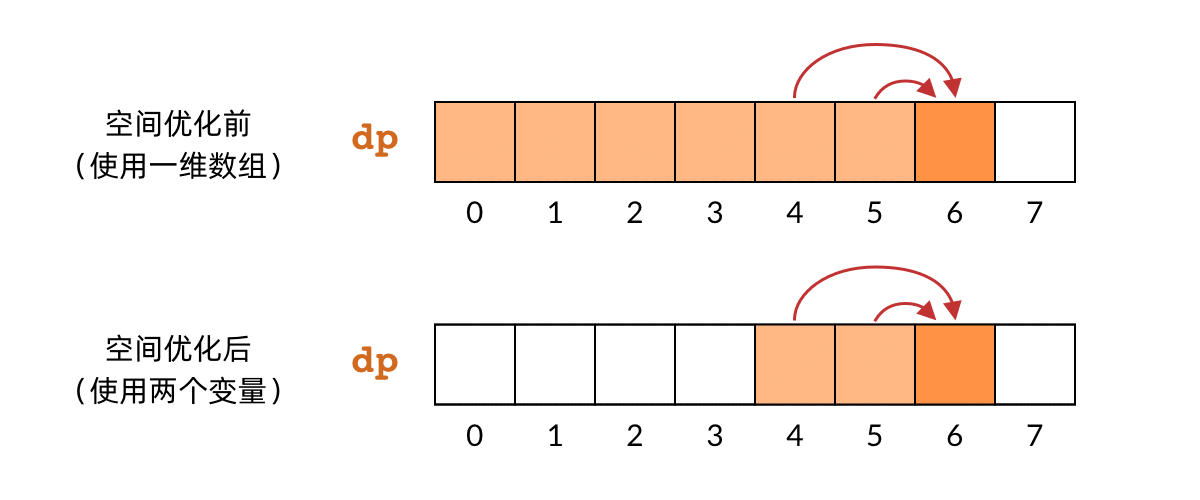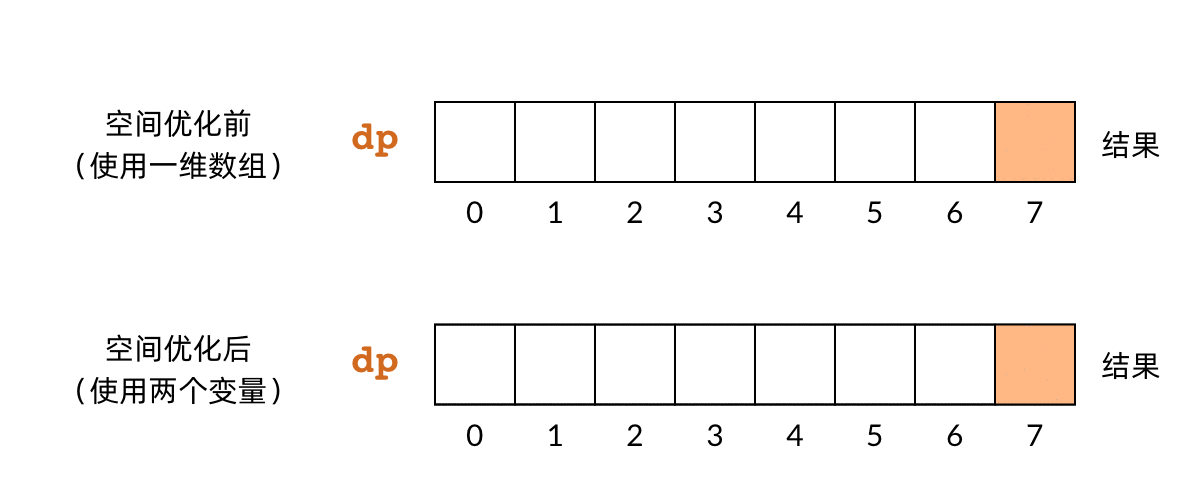
3dcbb1028ed9cdac95fdc8c8348ccc6f2e4c50b3fd8222e5690257d6b495090a

Approach1

[7,2,3,9,1] ==> max: 7+9

def rob(nums: List[int]) -> int:
    if len(nums) == 0:
        return 0

    # 子问题：
    # f(k) = 偷 [0..k) 房间中的最大金额

    # f(0) = 0
    # f(1) = nums[0]
    # f(k) = max{ rob(k-1), nums[k-1] + rob(k-2) }

    res = [0] * (len(nums)+1)
    res[0] = 0
    res[1] = nums[0]
    for k in range(2, len(nums)+1):
        res[k] = max(res[k-1], nums[k-1] + res[k-2])
    return res[len(nums)]

Approach2

def rob(self, nums: List[int]) -> int:
    cur, pre = 0, 0
    for num in nums:
        cur, pre = max(pre + num, cur), cur
    return cur

时间复杂度 O(N) ： 遍历 nums 需要线性时间 空间复杂度 O(1) ： cur和 pre 使用常数大小的额外空间