LeetCode day7

2020-05-01 4 minutes read

LeetCode

#LeetCode

views 778 words

160. Intersection of Two Linked Lists

Topic: Linked list

Write a program to find the node at which the intersection of two singly linked lists begins.

For example, the following two linked lists:

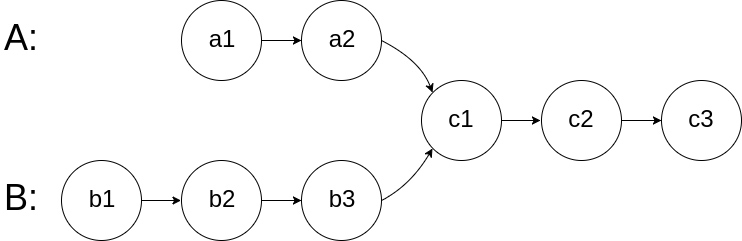begin to intersect at node c1.

Example 1:

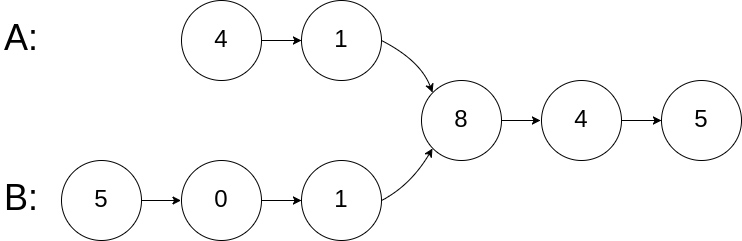
Input: intersectVal = 8, listA = [4,1,8,4,5], listB = [5,0,1,8,4,5], skipA = 2, skipB = 3
Output: Reference of the node with value = 8
Input Explanation: The intersected node's value is 8 (note that this must not be 0 if the two lists intersect). From the head of A, it reads as [4,1,8,4,5]. From the head of B, it reads as [5,0,1,8,4,5]. There are 2 nodes before the intersected node in A; There are 3 nodes before the intersected node in B.

Example 2:

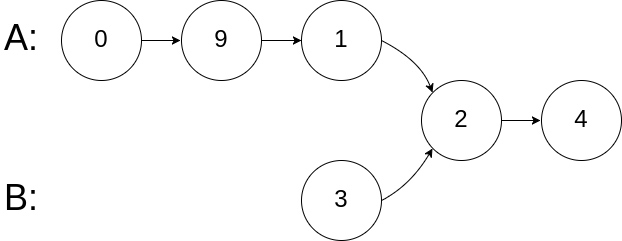
Input: intersectVal = 2, listA = [0,9,1,2,4], listB = [3,2,4], skipA = 3, skipB = 1
Output: Reference of the node with value = 2
Input Explanation: The intersected node's value is 2 (note that this must not be 0 if the two lists intersect). From the head of A, it reads as [0,9,1,2,4]. From the head of B, it reads as [3,2,4]. There are 3 nodes before the intersected node in A; There are 1 node before the intersected node in B.

Example 3:

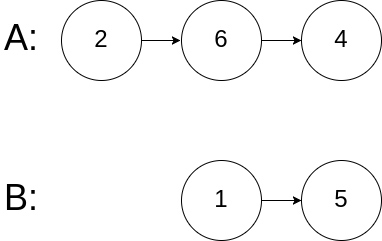
Input: intersectVal = 0, listA = [2,6,4], listB = [1,5], skipA = 3, skipB = 2
Output: null
Input Explanation: From the head of A, it reads as [2,6,4]. From the head of B, it reads as [1,5]. Since the two lists do not intersect, intersectVal must be 0, while skipA and skipB can be arbitrary values.
Explanation: The two lists do not intersect, so return null.

Notes:

If the two linked lists have no intersection at all, return null.
The linked lists must retain their original structure after the function returns.
You may assume there are no cycles anywhere in the entire linked structure.
Your code should preferably run in O(n) time and use only O(1) memory.

Approach1

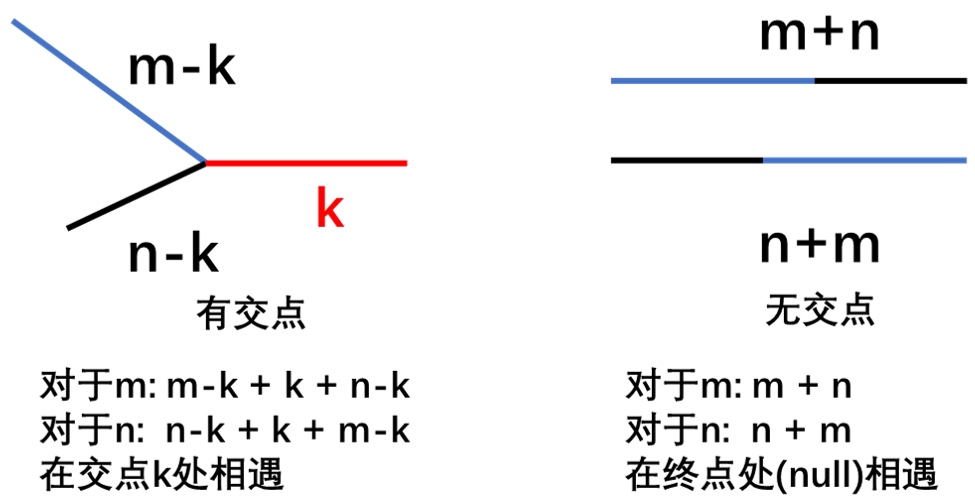
通常做这种题的思路是分别为链表A和链表B设置指针A和指针B，然后开始遍历链表，如果遍历完当前链表，则将指针指向另外一个链表的头部继续遍历，直至两个指针相遇.

值得注意的是，无论是相交还是不相交，对于无环的链表来说，都一定会相遇，因此不会死循环

def getIntersectionNode(headA, headB):
    ha, hb = headA, headB
    while ha != hb:
        ha = ha.next if ha else headB
        hb = hb.next if hb else headA
    return ha

169. Majority Element

Topic: Bit manipulation, Array, Divide and Conquer

Given an array of size n, find the majority element. The majority element is the element that appears more than ⌊ n/2 ⌋ times.

You may assume that the array is non-empty and the majority element always exist in the array.

Example 1:

Input: [3,2,3]
Output: 3

Example 2:

Input: [2,2,1,1,1,2,2]
Output: 2

Approach1

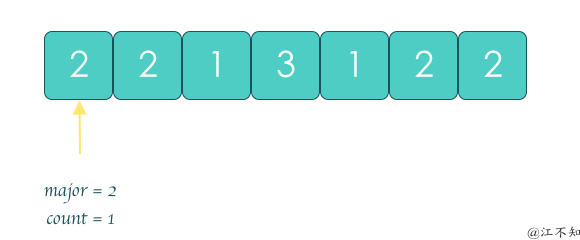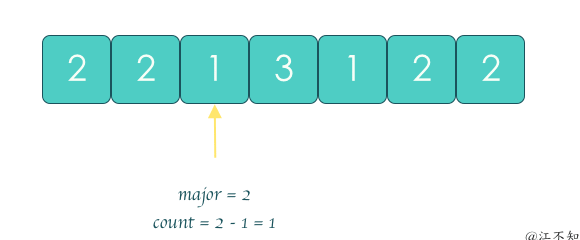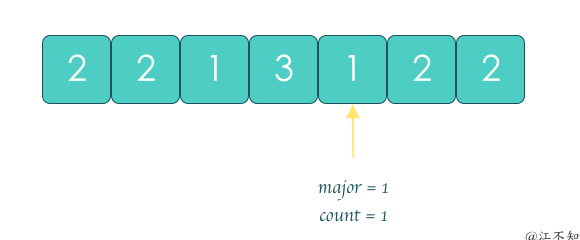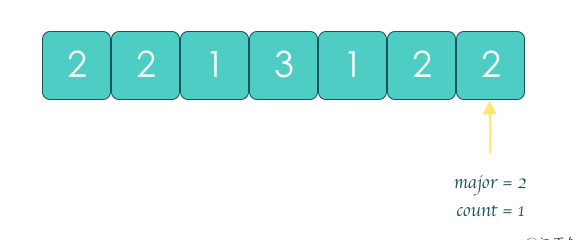
投票算法: 通过不断消除不同元素直到没有不同元素, 剩下的元素就是要找的元素.

Boyer–Moore-majority-vote-algorith

def majorityElement(nums: List[int]) -> int:  
    major = nums[0]
    count = 1
    for i in nums[1:]:
        if i == major:
            count+= 1
        elif count == 0:
            major = i
        else:
            count -= 1
    return major

时间复杂度：O(N)，其中N为数组长度空间复杂度：O(1)

Approach2

dic (这个方法严格要求major是 more than [n/2], 而上面的投票法只是求众数) E.g. [2,4,1,3,1,2,2] dic方法的输出是null, 而投票法的输出是2

def majorityElement(nums: List[int]) -> int:
    n = len(nums)
    dic = {}
    for i in range(n):
        dic[nums[i]] = dic.get(nums[i],0) + 1
        if dic[nums[i]] > n/2:
            return nums[i]

171. Excel Sheet Column Number

Topic: Math

Given a column title as appear in an Excel sheet, return its corresponding column number.

For example:

    A -> 1
    B -> 2
    C -> 3
    ...
    Z -> 26
    AA -> 27
    AB -> 28 
    ...

Example 1:

Input: "A"
Output: 1

Example 2:

Input: "AB"
Output: 28

Example 3:

Input: "ZY"
Output: 701

Approach1

26进制转十进制

ord() :返回对应的 ASCII 数值, ord(‘a’) –> 97, ord(‘A’) –> 65

def titleToNumber(s: str) -> int:
    res = 0
    bit = 1
    for a in s[::-1]:  # 从左到右
        res += (ord(a) - 64) * bit  # i.e. 'A'-> 65 - 64 = 1
        bit *= 26
    return res

Approach2

same but neat

def titleToNumber(s: str) -> int:
    return sum( (ord(a) - 64) * (26 ** i)  for i, a in enumerate(s[::-1]))

Approach3

same but with ord()

def titleToNumber(s: str) -> int:
    tmp ={'A':1,'B':2,'C':3,'D':4,'E':5,'F':6,'G':7,'H':8,'I':9,'J':10,'K':11,'L':12,'M':13,'N':14,'O':15,'P':16,'Q':17,'R':18,'S':19,'T':20,'U':21,'V':22,'W':23,'X':24,'Y':25,'Z':26}
    s=[i for i in s]
    res=0
    p=1
    while s:
        res+=tmp[s.pop()]*p
        p=p*26
    return res

172. Factorial Trailing Zeroes

Topic: Math

Given an integer n, return the number of trailing zeroes in n!.

Example 1:

Input: 3
Output: 0
Explanation: 3! = 6, no trailing zero.

Example 2:

Input: 5
Output: 1
Explanation: 5! = 120, one trailing zero.

Note: Your solution should be in logarithmic time complexity.

Approach1

要在末位产生0，则必然是5×2.

找到了n中是5倍数的所有数，例如25，即在25!中找到了5个是5的倍数的数分别为5,10,15,20,25

def trailingZeroes(n: int) -> int:
    p = 0
    while n >= 5:
        n = n // 5
        p += n
    return p

Approach2

my, but if n too big, then overtime.

def trailingZeroes(n: int) -> int:
    res = 1
    cnt = 0
    for i in range(1,n+1):
        res *= i
    for j in str(res)[::-1]:
        if j =='0':
            cnt += 1
        else:
            break
    return cnt