LeetCode day5

2020-04-29 4 minutes read

views 804 words

108. Convert Sorted Array to Binary Search Tree

Topic: Tree, Depth-first Search

Given an array where elements are sorted in ascending order, convert it to a height balanced BST.

For this problem, a height-balanced binary tree is defined as a binary tree in which the depth of the two subtrees of every node never differ by more than 1.

Example:

Given the sorted array: [-10,-3,0,5,9],

One possible answer is: [0,-3,9,-10,null,5], which represents the following height balanced BST:

      0
     / \
   -3   9
   /   /
 -10  5

Approach1

recursive:

def sortedArrayToBST(self, nums: List[int]) -> TreeNode:
    if not nums:
        return None
    
    mid = len(nums) // 2
    
    root = TreeNode(nums[mid])
    
    root.left = self.sortedArrayToBST(nums[:mid])            
    root.right = self.sortedArrayToBST(nums[mid+1:])
    
    return root

This might be nice and easy to code up, but the asymptotic complexity is bad. Slices take O(s) where ’s’ is the size of the slice. Therefore this algorithm has runtime O(n lg n), space O(n)

118. Pascal’s Triangle

Topic: Array

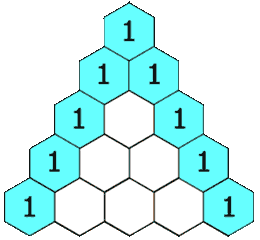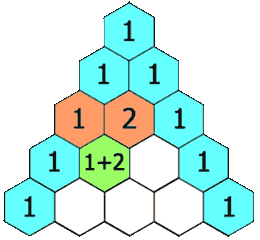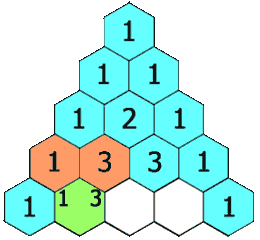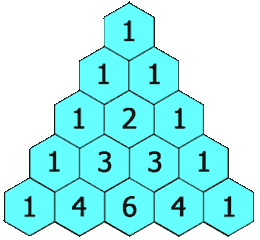
PascalTriangleAnimated2

Given a non-negative integer numRows, generate the first numRows of Pascal’s triangle.

In Pascal’s triangle, each number is the sum of the two numbers directly above it.

Example:

Input: 5
Output:
[
     [1],
    [1,1],
   [1,2,1],
  [1,3,3,1],
 [1,4,6,4,1]
]

Approach1

def generate(numRows: int) -> List[List[int]]:
    if numRows <= 0:
        return []
    pascal = [[1]*(i+1) for i in range(numRows)]
    for i in range(numRows):
        for j in range(1,i):
            pascal[i][j] = pascal[i-1][j-1] + pascal[i-1][j]
    return pascal

Approach2

Faster:

def generate(numRows: int) -> List[List[int]]:
    if not numRows: return []
    ret = [[1]]
    numRows -= 1
    while numRows:
        ret.append([1] + [a+b for a,b in zip(ret[-1][:-1], ret[-1][1:])] +[1])
        numRows-=1
    return ret

Approach3

def generate(numRows: int) -> List[List[int]]:
    if numRows == 0:
        return []
    elif numRows == 1:
        return [[1]]
    
    res = [[1],[1,1]]
    for i in range(1,numRows-1):
        tmp = [1]
        for j in range(len(res[i])-1):
            tmp.append(res[i][j]+res[i][j+1])
        tmp.append(1)
        res.append(tmp)
    return res

121. Best Time to Buy and Sell Stock

Topic: Array, Dynamic Programming

Say you have an array for which the ith element is the price of a given stock on day i.

If you were only permitted to complete at most one transaction (i.e., buy one and sell one share of the stock), design an algorithm to find the maximum profit.

Note that you cannot sell a stock before you buy one.

Example1:

Input: [7,1,5,3,6,4]
Output: 5
Explanation: Buy on day 2 (price = 1) and sell on day 5 (price = 6), profit = 6-1 = 5.
             Not 7-1 = 6, as selling price needs to be larger than buying price.

Example2:

Input: [7,6,4,3,1]
Output: 0
Explanation: In this case, no transaction is done, i.e. max profit = 0.

Approach1

def maxProfit(prices: List[int]) -> int:
    profit = [0]
    for i in range(1,len(prices)):
        if prices[i] > min(prices[:i]):
            profit.append(max(profit[i-1],prices[i] - min(prices[:i])))
        else:
            profit.append(-1)
    return max(profit)

Approach2

neat - iterative

def maxProfit(prices: List[int]) -> int:
    minprice = float('inf')
    maxprofit = 0
    for price in prices:
        minprice = min(minprice, price)
        maxprofit = max(maxprofit, price - minprice)
    return maxprofit

时间复杂度： $\mathcal{O}(n)$ ，遍历了一遍数组空间复杂度： $\mathcal{O}(1)$ ，使用了有限的变量

Approach3

def maxProfit(prices: List[int]) -> int:
    n = len(prices)
    if n == 0: return 0 # 边界条件
    dp = [0] * n
    minprice = prices[0] 

    for i in range(1, n):
        minprice = min(minprice, prices[i])
        dp[i] = max(dp[i - 1], prices[i] - minprice)

    return dp[-1]

时间复杂度： $\mathcal{O}(n)$ 空间复杂度： $\mathcal{O}(n)$

122. Best Time to Buy and Sell Stock II

Topic: Greedy, Array

Say you have an array prices for which the ith element is the price of a given stock on day i.

Design an algorithm to find the maximum profit. You may complete as many transactions as you like (i.e., buy one and sell one share of the stock multiple times).

Note: You may not engage in multiple transactions at the same time (i.e., you must sell the stock before you buy again).

Example 1:

Input: [7,1,5,3,6,4]
Output: 7
Explanation: Buy on day 2 (price = 1) and sell on day 3 (price = 5), profit = 5-1 = 4.
             Then buy on day 4 (price = 3) and sell on day 5 (price = 6), profit = 6-3 = 3.

Example 2:

Input: [1,2,3,4,5]
Output: 4
Explanation: Buy on day 1 (price = 1) and sell on day 5 (price = 5), profit = 5-1 = 4.
             Note that you cannot buy on day 1, buy on day 2 and sell them later, as you are
             engaging multiple transactions at the same time. You must sell before buying again.

连续上涨交易日 == 等价于每天都买卖

Example 3:

Input: [7,6,4,3,1]
Output: 0
Explanation: In this case, no transaction is done, i.e. max profit = 0.

Constraints:

1 <= prices.length <= 3 * 10 ^ 4
0 <= prices[i] <= 10 ^ 4

Approach1

def maxProfit( prices: List[int]) -> int:
    res = []
    for i in range(1,len(prices)):
        if prices[i] > prices[i-1]:
            res.append(prices[i] - prices[i-1])
    return sum(res)

Approach2

neat but same

def maxProfit(prices: List[int]) -> int:
    return sum(prices[i]-prices[i-1] for i in range(1,len(prices)) if prices[i]-prices[i-1]>0)