LeetCode day27
Diffculty: Medium
240. Search a 2D Matrix II
Topic: Binary, Divide and Conquer
Write an efficient algorithm that searches for a value in an m x n matrix. This matrix has the following properties:
- Integers in each row are sorted in ascending from left to right.
- Integers in each column are sorted in ascending from top to bottom.
Example:
Consider the following matrix:
[
[1, 4, 7, 11, 15],
[2, 5, 8, 12, 19],
[3, 6, 9, 16, 22],
[10, 13, 14, 17, 24],
[18, 21, 23, 26, 30]
]Given target = 5, return true.
Given target = 20, return false.
Approach1
def searchMatrix(matrix, target):
"""
:type matrix: List[List[int]]
:type target: int
:rtype: bool
"""
if not matrix:
return False
row = len(matrix) - 1
col = 0
while row >= 0 and col <= len(matrix[0]) - 1:
if matrix[row][col] > target:
row -= 1
elif matrix[row][col] < target:
col += 1
else:
return True
return False时间复杂度:O(n+m)。 时间复杂度分析的关键是注意到在每次迭代(不返回 true)时,行或列都会精确地递减/递增一次。由于行只能减少 m 次,而列只能增加 n 次,因此在导致 while 循环终止之前,循环不能运行超过 n+m 次。因为所有其他的工作都是常数,所以总的时间复杂度在矩阵维数之和中是线性的。
空间复杂度:O(1),因为这种方法只处理几个指针,所以它的内存占用是恒定的
Approach2
brute forch
def searchMatrix(matrix, target):
"""
:type matrix: List[List[int]]
:type target: int
:rtype: bool
"""
if not matrix:
return False
row = len(matrix)
col = len(matrix[0])
for i in range(row):
for j in range(col):
if target == matrix[i][j]:
return True
return False时间复杂度:O(mn)。因为我们在 n×m 矩阵上操作,总的时间复杂度为矩阵的大小 空间复杂度:O(1),暴力法分配的额外空间不超过少量指针,因此内存占用是恒定的
Approach2
brute forch
def searchMatrix(matrix, target):
"""
:type matrix: List[List[int]]
:type target: int
:rtype: bool
"""
251. Flatten 2D Vector
Topic: design
Design and implement an iterator to flatten a 2d vector. For example, Given 2d vector =
[
[1,2],
[3],
[4,5,6]
]By calling next repeatedly until hasNext returns false, the order of elements returned by next should be: [1,2,3,4,5,6].
Example:
Vector2D iterator = new Vector2D([[1,2],[3],[4]])
iterator.next(); // return 1
iterator.next(); // return 2
iterator.next(); // return 3
iterator.hasNext(); // return true
iterator.hasNext(); // return true
iterator.next(); // return 4
iterator.hasNext(); // return falseHint:
1. How many variables do you need to keep track?
2. Two variables is all you need. Try with x and y.
3. Beware of empty rows. It could be the first few rows.
4. To write correct code, think about the invariant to maintain. What is it?
5. The invariant is x and y must always point to a valid point in the 2d vector. Should you maintain your invariant ahead of time or right when you need it?
6. Not sure? Think about how you would implement hasNext(). Which is more complex?
7. Common logic in two different places should be refactored into a common method.Follow up: As an added challenge, try to code it using only iterators in C++ or iterators in Java.
Approach1
class Vector2D(object):
def __init__(self, vec2d):
"""
Initialize your data structure here.
:type vec2d: List[List[int]]
"""
self.vec2d = vec2d
self.i1 = 0 # outer level index
self.i2 = 0 # inner level index
self._moveToValid()
def _moveToValid(self):
"""
move i1 and i2 to a valid position, so that self.vec2d[self.i1][self.i2] is valid (i1,i2分别是row和col的index, col的长度不是固定的, 所以是len(self.vec2d[self.i1]), 当i2大于这个长度, 就跳到下一行(row+=1),i2指向第一个index(i2=0))
"""
while self.i1 < len(self.vec2d) and self.i2 >= len(self.vec2d[self.i1]):
self.i1 += 1
self.i2 = 0
def next(self):
"""
:rtype: int
"""
ret = self.vec2d[self.i1][self.i2]
self.i2 += 1
self._moveToValid()
return ret
def hasNext(self):
"""
:rtype: bool
"""
return self.i1 < len(self.vec2d)
# Your Vector2D object will be instantiated and called as such:
# obj = Vector2D(v)
# param_1 = obj.next()
# param_1 = obj.hasNext()253. Meeting Rooms II 会议室之二
Topic: heap
Given an array of meeting time intervals consisting of start and end times [[s1,e1],[s2,e2],…] (si < ei), find the minimum number of conference rooms required.
Example 1:
Input: [[0, 30],[5, 10],[15, 20]]
Output: 2Example 2:
Input: [[7,10],[2,4]]
Output: 1Approach1
from heapq import heappush, heappop
def minMeetingRooms(intervals):
"""
:type intervals: List[Interval]
:rtype: int
"""
SI = sorted(intervals, key=lambda it: (it.start, it.end)) # sorted intervals
ret = 0
heap = [] # contains end times
for it in SI:
start, end = it.start, it.end
while heap and heap[0] <= start:
heappop(heap)
heappush(heap, end)
ret = max(ret, len(heap))
return ret277. Find the Celebrity
Topic:
Suppose you are at a party with n people (labeled from 0 to n - 1) and among them, there may exist one celebrity. The definition of a celebrity is that all the other n - 1 people know him/her but he/she does not know any of them.
Now you want to find out who the celebrity is or verify that there is not one. The only thing you are allowed to do is to ask questions like: “Hi, A. Do you know B?” to get information of whether A knows B. You need to find out the celebrity (or verify there is not one) by asking as few questions as possible (in the asymptotic sense).
You are given a helper function bool knows(a, b)which tells you whether A knows B. Implement a function int findCelebrity(n). There will be exactly one celebrity if he/she is in the party. Return the celebrity’s label if there is a celebrity in the party. If there is no celebrity, return -1.
Example 1:
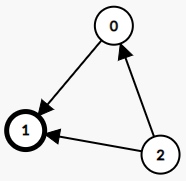
Input: graph = [
[1,1,0],
[0,1,0],
[1,1,1]
]
Output: 1
Explanation: There are three persons labeled with 0, 1 and 2. graph[i][j] = 1 means person i knows person j, otherwise graph[i][j] = 0 means person i does not know person j. The celebrity is the person labeled as 1 because both 0 and 2 know him but 1 does not know anybody.Example 2:
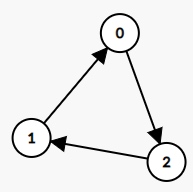
Input: graph = [
[1,0,1],
[1,1,0],
[0,1,1]
]
Output: -1
Explanation: There is no celebrity.Note:
- The directed graph is represented as an adjacency matrix, which is an n x n matrix where a[i][j] = 1 means person i knows person j while a[i][j] = 0 means the contrary.
- Remember that you won’t have direct access to the adjacency matrix.
Approach1
class Solution(object):
def knows(self, a, b, cache):
cacheKey = (a,b)
if cacheKey not in cache:
cache[cacheKey] = knows(a,b)
return cache[cacheKey]
def findCelebrity(self, n):
"""
:type n: int
:rtype: int
"""
candidate = 0
cache = dict()
for person in range(1,n):
if self.knows(candidate, person, cache):
candidate = person
if all( ( self.knows(person, candidate, cache) and not self.knows(candidate, person, cache) )
for person in range(0,n) if person != candidate ):
return candidate
else:
return -1