LeetCode day23

2020-05-17 7 minutes read

LeetCode

#LeetCode

views 1280 words

Diffculty: Medium

148. Sort List

Topic: Sort, Linked list

Sort a linked list in O(n log n) time using constant space complexity.

Example 1:

Input: 4->2->1->3
Output: 1->2->3->4

Example 2:

Input: -1->5->3->4->0
Output: -1->0->3->4->5

Approach1

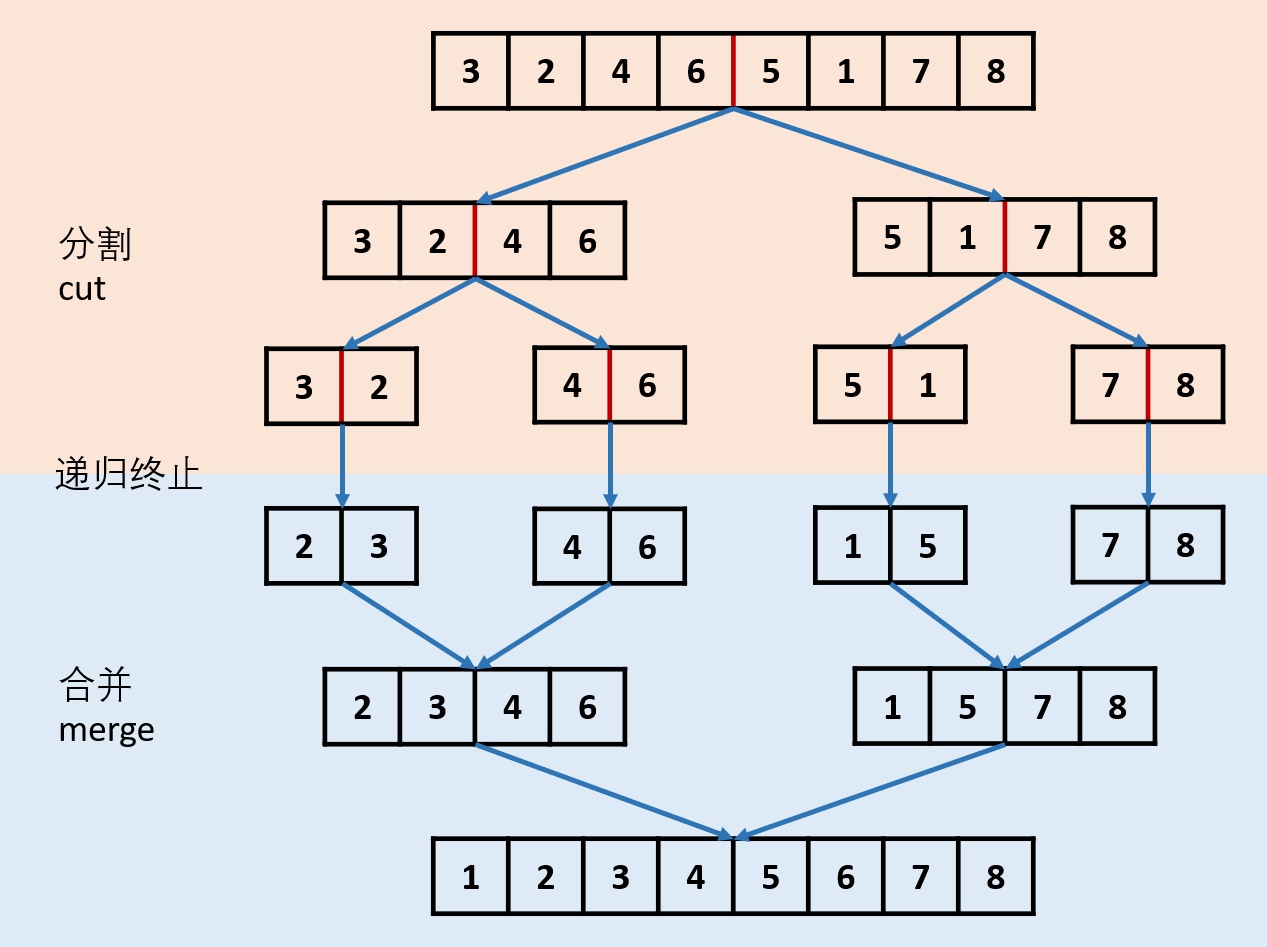
题目要求时间空间复杂度分别为O(nlogn)和O(1)，根据时间复杂度自然想到二分法，从而联想到归并排序
对数组做归并排序的空间复杂度为 O(n)O(n)，分别由新开辟数组O(n)O(n)和递归函数调用O(logn)O(logn)组成，而根据链表特性
- 数组额外空间：链表可以通过修改引用来更改节点顺序，无需像数组一样开辟额外空间；
- 递归额外空间：递归调用函数将带来O(logn)的空间复杂度，因此若希望达到O(1)空间复杂度，则不能使用递归。
通过递归实现链表归并排序，有以下两个环节：
- 分割 cut 环节：找到当前链表中点，并从中点将链表断开（以便在下次递归 cut 时，链表片段拥有正确边界）；
  - 我们使用 fast,slow 快慢双指针法，奇数个节点找到中点，偶数个节点找到中心左边的节点。
  - 找到中点 slow 后，执行 slow.next = None 将链表切断。
  - 递归分割时，输入当前链表左端点 head 和中心节点 slow 的下一个节点 tmp(因为链表是从 slow 切断的)。
  - cut 递归终止条件：当head.next == None时，说明只有一个节点了，直接返回此节点。
- 合并 merge 环节：将两个排序链表合并，转化为一个排序链表。
  - 双指针法合并，建立辅助ListNode h 作为头部。
  - 设置两指针 left, right 分别指向两链表头部，比较两指针处节点值大小，由小到大加入合并链表头部，指针交替前进，直至添加完两个链表。
  - 返回辅助ListNode h 作为头部的下个节点 h.next。
  - 时间复杂度 O(l + r)，l, r 分别代表两个链表长度。
- 当题目输入的 head == None 时，直接返回None。

def sortList(self, head: ListNode) -> ListNode:
    if not head or not head.next: return head # termination.
    # cut the LinkedList at the mid index.
    slow, fast = head, head.next
    while fast and fast.next:
        fast, slow = fast.next.next, slow.next
    mid, slow.next = slow.next, None # save and cut.
    # recursive for cutting.
    left, right = self.sortList(head), self.sortList(mid)
    # merge `left` and `right` linked list and return it.
    h = res = ListNode(0)
    while left and right:
        if left.val < right.val: h.next, left = left, left.next
        else: h.next, right = right, right.next
        h = h.next
    h.next = left if left else right
    return res.next

Approach2

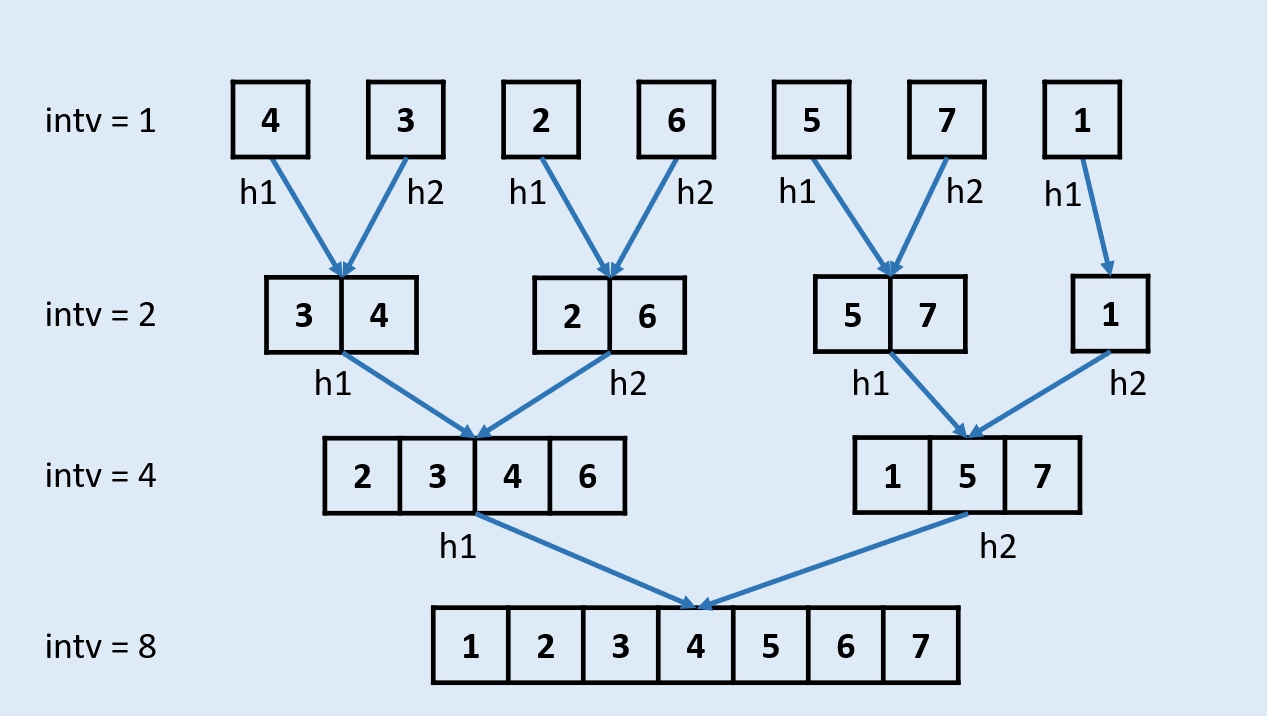
对于非递归的归并排序，需要使用迭代的方式替换cut环节：
- cut环节本质上是通过二分法得到链表最小节点单元，再通过多轮合并得到排序结果。
- 每一轮合并merge操作针对的单元都有固定长度intv，例如：
  - 第一轮合并时intv = 1，即将整个链表切分为多个长度为1的单元，并按顺序两两排序合并，合并完成的已排序单元长度为2。
  - 第二轮合并时intv = 2，即将整个链表切分为多个长度为2的单元，并按顺序两两排序合并，合并完成已排序单元长度为4。
  - 以此类推，直到单元长度intv >= 链表长度，代表已经排序完成。
- 根据以上推论，可以仅根据intv计算每个单元边界，并完成链表的每轮排序合并，例如:
  - 当intv = 1时，将链表第1和第2节点排序合并，第3和第4节点排序合并，……。
  - 当intv = 2时，将链表第1-2和第3-4节点排序合并，第5-6和第7-8节点排序合并，……。
  - 当intv = 4时，将链表第1-4和第5-8节点排序合并，第9-12和第13-16节点排序合并，……。
此方法时间复杂度O(nlogn)，空间复杂度O(1)

模拟上述的多轮排序合并：
- 统计链表长度length，用于通过判断intv < length判定是否完成排序；
- 额外声明一个节点res，作为头部后面接整个链表，用于：
  - intv *= 2即切换到下一轮合并时，可通过res.next找到链表头部h；
  - 执行排序合并时，需要一个辅助节点作为头部，而res则作为链表头部排序合并时的辅助头部pre；后面的合并排序可以将上次合并排序的尾部tail用做辅助节点。
- 在每轮intv下的合并流程：
  1. 根据intv找到合并单元1和单元2的头部h1, h2。由于链表长度可能不是2^n，需要考虑边界条件：
    - 在找h2过程中，如果链表剩余元素个数少于intv，则无需合并环节，直接break，执行下一轮合并；
    - 若h2存在，但以h2为头部的剩余元素个数少于intv，也执行合并环节，h2单元的长度为c2 = intv - i。
  2. 合并长度为c1, c2的h1, h2链表，其中：
    - 合并完后，需要修改新的合并单元的尾部pre指针指向下一个合并单元头部h。（在寻找h1, h2环节中，h指针已经被移动到下一个单元头部）
    - 合并单元尾部同时也作为下次合并的辅助头部pre。
  3. 当h == None，代表此轮intv合并完成，跳出。
- 每轮合并完成后将单元长度×2，切换到下轮合并：intv *= 2

code:

def sortList(self, head: ListNode) -> ListNode:
    h, length, intv = head, 0, 1
    while h: h, length = h.next, length + 1
    res = ListNode(0)
    res.next = head
    # merge the list in different intv.
    while intv < length:
        pre, h = res, res.next
        while h:
            # get the two merge head `h1`, `h2`
            h1, i = h, intv
            while i and h: h, i = h.next, i - 1
            if i: break # no need to merge because the `h2` is None.
            h2, i = h, intv
            while i and h: h, i = h.next, i - 1
            c1, c2 = intv, intv - i # the `c2`: length of `h2` can be small than the `intv`.
            # merge the `h1` and `h2`.
            while c1 and c2:
                if h1.val < h2.val: pre.next, h1, c1 = h1, h1.next, c1 - 1
                else: pre.next, h2, c2 = h2, h2.next, c2 - 1
                pre = pre.next
            pre.next = h1 if c1 else h2
            while c1 > 0 or c2 > 0: pre, c1, c2 = pre.next, c1 - 1, c2 - 1
            pre.next = h 
        intv *= 2
    return res.next

150. Evaluate Reverse Polish Notation

Topic: Stack

Evaluate the value of an arithmetic expression in Reverse Polish Notation.

Valid operators are +, -, *, /. Each operand may be an integer or another expression.

Note:

Division between two integers should truncate toward zero.
The given RPN expression is always valid. That means the expression would always evaluate to a result and there won’t be any divide by zero operation.

Example 1:

Input: ["2", "1", "+", "3", "*"]
Output: 9
Explanation: ((2 + 1) * 3) = 9

Example 2:

Input: ["4", "13", "5", "/", "+"]
Output: 6
Explanation: (4 + (13 / 5)) = 6

Example 3:

Input: ["10", "6", "9", "3", "+", "-11", "*", "/", "*", "17", "+", "5", "+"]
Output: 22
Explanation: 
  ((10 * (6 / ((9 + 3) * -11))) + 17) + 5
= ((10 * (6 / (12 * -11))) + 17) + 5
= ((10 * (6 / -132)) + 17) + 5
= ((10 * 0) + 17) + 5
= (0 + 17) + 5
= 17 + 5
= 22

RPN -w1262

Approach1

def evalRPN(tokens: List[str]) -> int:
    if len(tokens) == 0: return 0
    stack = []  # last in, first out
    oper = ['+','-','*','/']
    for i in tokens:
        if i not in oper:
            stack.append(int(i))
        else:
            # print(stack)
            tmp1 = str(stack.pop())
            tmp2 = str(stack.pop())
            res = int(eval(tmp2 + i + tmp1))
            stack.append(res)
    return stack[0]

Approach2

上面用了eval, 太慢

def evalRPN(tokens: List[str]) -> int:
    stack = []
    plus = lambda a, b : b + a
    sub = lambda a, b: b - a
    mul = lambda a, b: b * a
    div = lambda a, b: int(b / a)
    opt = {
        "+": plus,
        "-": sub,
        "*": mul,
        "/": div
    }
    for t in tokens:
        if t in opt:
            stack.append(opt[t](stack.pop(), stack.pop()))
        else:
            stack.append(int(t))
    return stack.pop()

152. Maximum Product Subarray

Topic: DP, Array

Given an integer array nums, find the contiguous subarray within an array (containing at least one number) which has the largest product.

Example 1:

Input: [2,3,-2,4]
Output: 6
Explanation: [2,3] has the largest product 6.

Example 2:

Input: [-2,0,-1]
Output: 0
Explanation: The result cannot be 2, because [-2,-1] is not a subarray.

Approach1

DP, 只要记录前i的最小值, 和最大值, 那么 dp[i] = max(nums[i] * pre_max, nums[i] * pre_min, nums[i]), 这里0 不需要单独考虑, 因为当相乘不管最大值和最小值,都会置0

def maxProduct(nums: List[int]) -> int:
    if not nums: return 
    res = nums[0]
    pre_max = nums[0]
    pre_min = nums[0]
    for num in nums[1:]:
        cur_max = max(pre_max * num, pre_min * num, num)
        cur_min = min(pre_max * num, pre_min * num, num)
        res = max(res, cur_max)
        pre_max = cur_max
        pre_min = cur_min
    return res

Approach2

根据符号的个数

当负数个数为偶数时候，全部相乘一定最大

当负数个数为奇数时候，它的左右两边的负数个数一定为偶数，只需求两边最大值

当有 0 情况，重置为1就可以了

nums = [2,3,-2,4]
def maxProduct(nums: List[int]) -> int:
    reverse_nums = nums[::-1]
    for i in range(1, len(nums)):
        nums[i] *= nums[i - 1] or 1  # 当nums[i - 1] 为0 时, 就*= 1
        reverse_nums[i] *= reverse_nums[i - 1] or 1
    print(nums, reverse_nums) # [2, 6, -12, -48] [4, -8, -24, -48]
    return max(nums + reverse_nums)

Approach3

类似滑动窗口的感觉

product(i, j) = product(0, j) / product(0, i) 从数组 i 到 j 的累乘等于从数组开头到 j 的累乘除以从数组开头到 i 的累乘(这里先忽略 0 的情况)，要考虑三种情况

累乘的乘积等于 0，就要重新开始

累乘的乘积小于 0，要找到前面最大的负数，这样才能保住从 i 到 j 最大

累乘的乘积大于 0，要找到前面最小的正数，同理

def maxProduct(self, nums: List[int]) -> int:
    if not nums: return
    # 目前的累乘
    cur_pro = 1
    # 前面最小的正数
    min_pos = 1
    # 前面最大的负数
    max_neg = float("-inf")
    # 结果
    res = float("-inf")
    for num in nums:
        cur_pro *= num
        # 考虑三种情况
        # 大于0
        if cur_pro > 0:
            res = max(res, cur_pro // min_pos)
            min_pos = min(min_pos, cur_pro)
        # 小于0
        elif cur_pro < 0:
            if max_neg != float("-inf"):
                res = max(res, cur_pro // max_neg)
            else:
                res = max(res, num)
            max_neg = max(max_neg, cur_pro)
        # 等于0 
        else:
            cur_pro = 1
            min_pos = 1
            max_neg = float("-inf")
            res = max(res, num)
    return res

162. Find Peak Element

Topic: Array, Binary Search

A peak element is an element that is greater than its neighbors(大于左右相邻的元素).

Given an input array nums, where nums[i] ≠ nums[i+1], find a peak element and return its index.

The array may contain multiple peaks, in that case return the index to any one of the peaks is fine.

You may imagine that nums[-1] = nums[n] = -∞.

Example 1:

Input: nums = [1,2,3,1]
Output: 2
Explanation: 3 is a peak element and your function should return the index number 2.

Example 2:

Input: nums = [1,2,1,3,5,6,4]
Output: 1 or 5 
Explanation: Your function can return either index number 1 where the peak element is 2, 
             or index number 5 where the peak element is 6.

Note:

Your solution should be in logarithmic complexity.

Approach1

若找到一个值，右侧的下个值更大，则在右侧一定存在峰值，反之，自身或者左侧一定存在峰值。看到O(log(n))，想到二分法

def findPeakElement(nums: List[int]) -> int:
    l=0
    r=len(nums)-1
    while(l<r):
        mid=(l+r)//2
        if(nums[mid]>nums[mid+1]): # 说明左侧的值更大, 则nums[mid]或者左侧一定存在峰值
            r=mid
        else:  # 否则，说明右侧的值更大, 右侧粗在峰值
            l=mid+1
    return l

时间复杂度：O(log(n)) 空间复杂度：O(1)

Approach2

O(n)的一次遍历算法

def findPeakElement(self, nums):
    for i in range(1, len(nums)):
        if nums[i - 1] > nums[i]:
            return i - 1
    return len(nums) - 1
    
    # =============================================
    nums = [float("-inf")] + nums + [float("-inf")]
    n = len(nums)
    for i in range(1, n - 1):
        if nums[i - 1] < nums[i] and nums[i] > nums[i + 1]:
            return i - 1