Diffculty: Medium

Input: 
gas  = [1,2,3,4,5]
cost = [3,4,5,1,2]

Output: 3

Explanation:
Start at station 3 (index 3) and fill up with 4 unit of gas. Your tank = 0 + 4 = 4
Travel to station 4. Your tank = 4 - 1 + 5 = 8
Travel to station 0. Your tank = 8 - 2 + 1 = 7
Travel to station 1. Your tank = 7 - 3 + 2 = 6
Travel to station 2. Your tank = 6 - 4 + 3 = 5
Travel to station 3. The cost is 5. Your gas is just enough to travel back to station 3.
Therefore, return 3 as the starting index.

Input: 
gas  = [2,3,4]
cost = [3,4,3]

Output: -1

Explanation:
You can't start at station 0 or 1, as there is not enough gas to travel to the next station.
Let's start at station 2 and fill up with 4 unit of gas. Your tank = 0 + 4 = 4
Travel to station 0. Your tank = 4 - 3 + 2 = 3
Travel to station 1. Your tank = 3 - 3 + 3 = 3
You cannot travel back to station 2, as it requires 4 unit of gas but you only have 3.
Therefore, you can't travel around the circuit once no matter where you start.

# print(2 % 5)  # 2
# print(-2 % 5)  # 3
# print(1%5)  # 1
# print(-1%5)  # 4

# s = 5
# s += 5-2
# print(s) # 8
def canCompleteCircuit(gas: List[int], cost: List[int]) -> int:
    # 环的长度
    mod = len(gas)

    # 起始点假设为 0，当前在 0 节点。
    start, cur = 0, 0

    # 把 0 节点的油都灌进去。
    oil = gas[0]

    # 当 cur + 1 == start 时说明到了终点，所以没有考虑终点到起点（两者相邻）所用的油。
    while (cur + 1) % mod != start:

        # 如果油不够开往下一节点。
        if oil < cost[cur]:
            # 说明以 start 为起始节点不行，将 start 前一位假设为起始节点。
            start = (start - 1) % mod
            # 新的起始点里面的油全都抱走，同时要计算从新的起始点
            # 到旧的的起始点（它的下一节点）所消耗的油。
            oil += gas[start] - cost[start]

        # 如果够。
        else:
            # 把消耗的油减掉。
            oil -= cost[cur]
            # 去下一个节点。
            cur = (cur + 1) % mod
            # 把新节点的油抱走。
            oil += gas[cur]
    
    # 返回时记得判断一下在终点时的油能否开到起点。
    return start if oil - cost[cur] >= 0 else -1

def canCompleteCircuit(gas: List[int], cost: List[int]) -> int:
    if sum(gas) < sum(cost):
        return -1
    n = len(gas)
    if n==1:
        return 0

    starts = [i for i in range(n) if gas[i] > cost[i]] # 所有可以出发的点
    start_idx = 0
    starts_len = len(starts)
    while True:
        start = starts[start_idx]
        gas_cur = gas[start]
        cost_cur = cost[start]
        tmp = (start+1) % n
        while tmp != start:
            if start_idx < starts_len and starts[start_idx] < tmp:
                start_idx += 1  #  # 更新下一个出发点
            
            gas_cur += gas[tmp]
            cost_cur += cost[tmp]
            if gas_cur < cost_cur:  # # 当前出发点失败，break, 重新出发（从更新过的i出发
                break
            tmp = (tmp +1) % n
        
        else:
            return start  # 当前出发点成功
        if start == starts[-1] and start_idx == n:  # 失败
            return -1

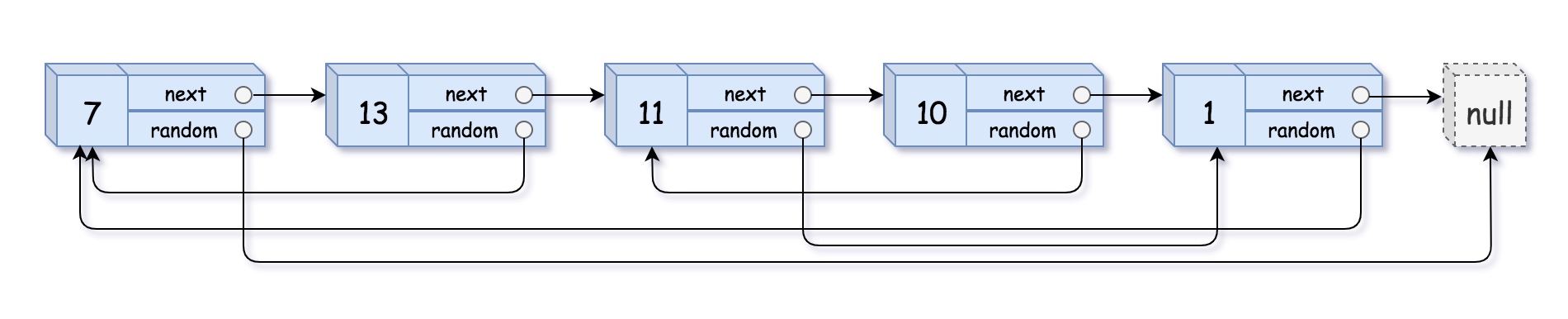
Input: head = [[7,null],[13,0],[11,4],[10,2],[1,0]]
Output: [[7,null],[13,0],[11,4],[10,2],[1,0]]

Input: head = [[1,1],[2,1]]
Output: [[1,1],[2,1]]

Input: head = [[3,null],[3,0],[3,null]]
Output: [[3,null],[3,0],[3,null]]

Input: head = []
Output: []
Explanation: Given linked list is empty (null pointer), so return null.

"""
# Definition for a Node.
class Node:
    def __init__(self, x: int, next: 'Node' = None, random: 'Node' = None):
        self.val = int(x)
        self.next = next
        self.random = random
"""

def copyRandomList(head: 'Node') -> 'Node':
    if not head:
        return None

    # 第一遍遍历，把每个新生成的结点放在对应的旧结点后面
    p = head
    while p:
        new_node = Node(p.val)
        new_node.next = p.next
        p.next = new_node

        p = new_node.next       # 下一个旧结点
    
    # 第二遍修改每个新结点的 next 和 random 
    p = head
    while p:
        next_origin = p.next.next        # 下一个旧结点备份一下
        p.next.next = next_origin.next if next_origin else None   # 修改新结点的 next
        p.next.random = p.random.next if p.random else None    # 修改新结点的 random

        p = next_origin         # 下一个旧结点
    
    return head.next

Input: s = "leetcode", wordDict = ["leet", "code"]
Output: true
Explanation: Return true because "leetcode" can be segmented as "leet code".

Input: s = "applepenapple", wordDict = ["apple", "pen"]
Output: true
Explanation: Return true because "applepenapple" can be segmented as "apple pen apple".
             Note that you are allowed to reuse a dictionary word.

Input: s = "catsandog", wordDict = ["cats", "dog", "sand", "and", "cat"]
Output: false

def wordBreak(s: str, wordDict: List[str]) -> bool:       
    n=len(s)
    dp=[False]*(n+1)
    dp[0]=True
    for i in range(n):
        for j in range(i+1,n+1):
            if(dp[i] and (s[i:j] in wordDict)):
                dp[j]=True
    return dp[-1]

def wordBreak(s: str, wordDict: List[str]) -> bool:
    import functools
    @functools.lru_cache(None)
    def back_track(s):
        if(not s):
            return True
        res=False
        for i in range(1,len(s)+1):
            if(s[:i] in wordDict):
                res=back_track(s[i:]) or res
        return res
    return back_track(s)

LRUCache cache = new LRUCache( 2 /* capacity */ );

cache.put(1, 1);
cache.put(2, 2);
cache.get(1);       // returns 1
cache.put(3, 3);    // evicts key 2
cache.get(2);       // returns -1 (not found)
cache.put(4, 4);    // evicts key 1
cache.get(1);       // returns -1 (not found)
cache.get(3);       // returns 3
cache.get(4);       // returns 4

from collections import OrderedDict
class LRUCache:
    def __init__(self, capacity: int):
        self.maxsize = capacity
        self.lrucache = OrderedDict()

    def get(self, key: int) -> int:
        # 说明在缓存中,重新移动字典的尾部
        if key in self.lrucache:
            self.lrucache.move_to_end(key)
        return self.lrucache.get(key, -1)  # get不到就返回-1
        
    def put(self, key: int, value: int) -> None:
        # 如果存在,删掉,重新赋值
        if key in self.lrucache:
            del self.lrucache[key]
        # 在字典尾部添加
        self.lrucache[key] = value
        if len(self.lrucache) > self.maxsize:
            # 弹出字典的头部(因为存储空间不够了)
            self.lrucache.popitem(last = False)  # FIFO order if false

# Your LRUCache object will be instantiated and called as such:
# obj = LRUCache(capacity)
# param_1 = obj.get(key)
# obj.put(key,value)

class Node:
    def __init__(self, key, val):
        self.key = key
        self.val = val
        self.prev = None
        self.next = None


class LRUCache:

    def __init__(self, capacity: int):
        # 构建首尾节点, 使之相连
        self.head = Node(0, 0)
        self.tail = Node(0, 0)
        self.head.next = self.tail
        self.tail.prev = self.head

        self.lookup = dict()
        self.max_len = capacity

    def get(self, key: int) -> int:
        if key in self.lookup:
            node = self.lookup[key]
            self.remove(node)
            self.add(node)
            return node.val
        else:
            return -1

    def put(self, key: int, value: int) -> None:
        if key in self.lookup:
            self.remove(self.lookup[key])
        if len(self.lookup) == self.max_len:
            # 把表头位置节点删除(说明最近的数据值)
            self.remove(self.head.next)
        self.add(Node(key, value))
    
    # 删除链表节点
    def remove(self, node):
        del self.lookup[node.key]
        node.prev.next = node.next
        node.next.prev = node.prev
    # 加在链表尾
    def add(self, node):
        self.lookup[node.key] = node
        pre_tail = self.tail.prev
        node.next = self.tail
        self.tail.prev = node
        pre_tail.next = node
        node.prev = pre_tail