LeetCode day19

4 minutes read
LeetCode
#LeetCode
views 822 words

Diffculty: Medium

78. Subsets

Topic: Array, Bit manipulation, Backtracking

Given a set of distinct integers, nums, return all possible subsets (the power set).

Note: The solution set must not contain duplicate subsets.

Example:

Input: nums = [1,2,3]
Output:
[
  [3],
  [1],
  [2],
  [1,2,3],
  [1,3],
  [2,3],
  [1,2],
  []
]

Approach1

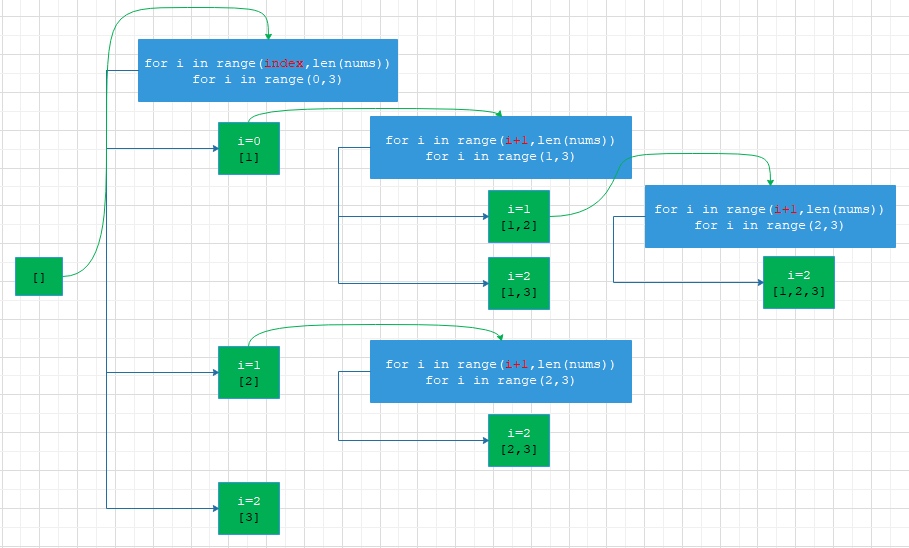
回溯三要素

  1. 有效结果
    • 没有条件，所有结果都是有效结果
    • res.append(path)
  2. 回溯范围及答案更新
    • 需要循环遍历，并且是部分遍历，只考虑当前元素之后的元素们，所以需要传入一个depth表示起点
    • ！！！depth仅用于表示起点，回溯的递归还是遍历的每个元素
    • 对于答案更新，依然是累加当前元素
    • for i in range(depth, len(nums)):
      • backtrack(path+[nums[i]], i+1) ## 一定要注意这里的递归传入是i+1，depth只是当前起点，不代表下一层范围

  3. 剪枝条件

    • 不需要剪枝

      def subsets(nums: List[int]) -> List[List[int]]:
    res = []
    
    def backtrack(depth,path):
        res.append(path)
        for i in range(depth,len(nums)):
            backtrack(i+1,path+[nums[i]])
                
    backtrack(0,[])
    # print(res)
    return res

Approach2

对于[1,2,3]，该如何枚举它的子集呢? 1选或不选，有两种情况，2选或不选，有两种情况，3选或不选，有两种情况，那么总共就是2*2*2=8种情况 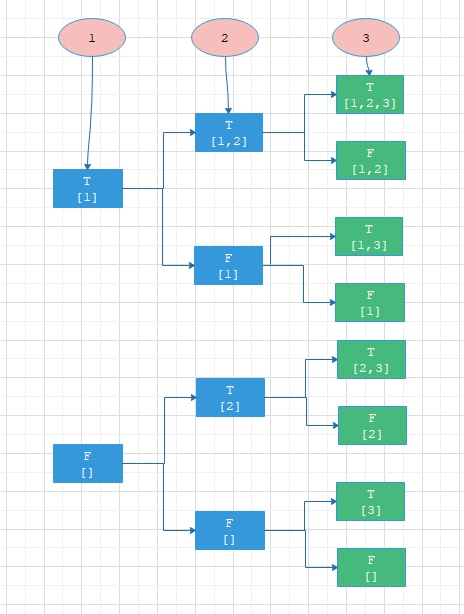绿色部分为答案

回溯三要素

  1. 有效结果
    • 当指向元素的depth==len(nums)的时候，就说明这一次的搜索结束了
  2. 回溯范围及答案更新
    • 不需要循环遍历，而只需要用一个index指向每一次的元素，下一层更新depth = depth+1
    • 对于答案更新，需要考虑选或不选当前答案，保存当前index指向的元素
      • backtrack(path+[nums[depth]], depth+1, nums)
      • backtrack(path, depth+1, nums)
  3. 剪枝条件
    • 不需要剪枝

不需要用遍历，但是又要对不同index进行判断，那么就传入一个depth变量进去，每次改变depth就可以了，用于指向每个元素

def subsets(self, nums: List[int]) -> List[List[int]]:
    self.res = []
    self.backtrack([], 0, nums)
    return self.res
    
def backtrack(self, sol, index, nums):
    if index == len(nums):
        self.res.append(sol)
        return
    
    self.backtrack(sol+[nums[index]], index+1, nums)
    self.backtrack(sol, index+1, nums)

Topic: Array, Backtracking

Given a 2D board and a word, find if the word exists in the grid.

The word can be constructed from letters of sequentially adjacent cell, where “adjacent” cells are those horizontally or vertically neighboring. The same letter cell may not be used more than once.

Example:

board =
[
  ['A','B','C','E'],
  ['S','F','C','S'],
  ['A','D','E','E']
]

Given word = "ABCCED", return true.
Given word = "SEE", return true.
Given word = "ABCB", return false.

Constraints:

  • board and word consists only of lowercase and uppercase English letters.
  • 1 <= board.length <= 200
  • 1 <= board[i].length <= 200
  • 1 <= word.length <= 10^3

Approach1

def exist(board: List[List[str]], word: str) -> bool:
    #         (x-1,y)
    # (x,y-1) (x,y) (x,y+1)
    #         (x+1,y)
    directions = [(0, -1), (-1, 0), (0, 1), (1, 0)]

    def backtrack(index,x,y,marked):
        # 递归终止条件
        if index == len(word) - 1:
            return board[x][y] == word[index]
            
        # 中间匹配了，再继续搜索
        if board[x][y] == word[index]:
            # 先占住这个位置，搜索不成功的话，要释放掉
            marked[x][y] = True
            for direction in directions:
                new_x = x + direction[0]
                new_y = y + direction[1]
                # 注意：如果这一次 search word 成功的话，就返回
                if 0 <= new_x < len(board) and 0 <= new_y < len(board[0]) and not marked[new_x][new_y] and backtrack(index+1,new_x,new_y,marked):
                    return True
            marked[x][y] = False
        return False


    marked = [[False for _ in range(len(board[0]))] for _ in range(len(board))]
    for i in range(len(board)):
        for j in range(len(board[0])):
            # 对每一个格子都从头开始搜索
            if backtrack(0,i,j,marked):
                return True
    return False

91. Decode Ways

Topic: String, DP

A message containing letters from A-Z is being encoded to numbers using the following mapping:

'A' -> 1
'B' -> 2
...
'Z' -> 26

Given a non-empty string containing only digits, determine the total number of ways to decode it.

Example 1:

Input: "12"
Output: 2
Explanation: It could be decoded as "AB" (1 2) or "L" (12).

Example 2:

Input: "226"
Output: 3
Explanation: It could be decoded as "BZ" (2 26), "VF" (22 6), or "BBF" (2 2 6).

Approach1

类似梯子题目 dp[i] = dp[i-1]+dp[i-2], 在这里是每次解码一个数字或者两个数字. 但是是有constraint的, 例如开头为’0’, 则不能解码, ‘0’之前大于’2’也不能解码, 例如’20’可以, ‘50’不行,

  • 输入 ‘12’ 的结果为 2，如果我们在 ‘12’ 后面增加一个数字 3，输入变成 ‘123’，结果是 ‘12’的结果 + ‘1’的结果 = 3

  • i 从索引 1 开始逐渐遍历 s，当前位置对应结果 = 上上次结果(如果 i 位置字符和 i-1 位置字符的组合满足条件) + 上次结果(如果 s[i] 不为 0)

    def numDecodings(s: str) -> int:
pp, p = 1, int(s[0] != '0')
for i in range(1, len(s)):
    pp, p = p, pp * (9 < int(s[i-1:i+1]) <= 26) + p * (int(s[i]) > 0)
return p

Approach2

动态转移公式可以写成：

  1. dp[i+1] = 0. if s[i] == ‘0’ and (s[i-1:i+1] < ‘10’ or s[i-1:i+1]>‘26’) 当前位置是0, 跟前一位合起来也不在 10-26 的范围内, 增加0次
  2. dp[i+1] = dp[i]. if s[i]!= ‘0’ and (s[i-1:i+1] < ‘10’ or s[i-1:i+1]>‘26’) 当前位置不是0, 跟前一位合起来也不在 10-26 的范围内, 增加0次
  3. dp[i+1] = dp[i-1]. if s[i] == ‘0’ and (s[i-1:i+1] >= ‘10’ and s[i-1:i+1]<=‘26’) 当前位置是0, 跟前一位合起来在 10-26 的范围内, 增加1次
  4. dp[i+1] = dp[i]+dp[i-1]. if s[i] != ‘0’ and (s[i-1:i+1] >= ‘10’ and s[i-1:i+1]<=‘26’) 当前位置不是0, 跟前一位合起来在 10-26 的范围内, 增加2次

code:

def numDecodings(s: str) -> int:
    n = len(s)
    if n==0: return 0
    dp = [1,0]
    dp[1] = 1 if s[0]!='0' else 0 
    for i in range(1,n):
        dp.append(0)
        if s[i]!='0':
            dp[i+1] += dp[i]
        if s[i-1:i+1]>='10' and s[i-1:i+1]<='26':
            dp[i+1] += dp[i-1]
    
    return dp[-1]

算法的时间代价为O(N),空间代价O(N)

优化: 可以保持dp数组的大小为2（因为再之前的数据是用不到的）

def numDecodings(s: str) -> int:
   n = len(s)
    if n==0: return 0
    dp = [1,0]
    dp[1] = 1 if s[0]!='0' else 0 
    for i in range(1,n):
        dp.append(0)
        if s[i]!='0':
            dp[-1] += dp[-2]
        if s[i-1:i+1]>='10' and s[i-1:i+1]<='26':
            dp[-1] += dp[-3]
        dp.pop(0)
    
    return dp[-1]

时间代价O(N),空间代价O(1)

94. Binary Tree Inorder Traversal

Topic: Stack, Tree, Hash Table

Given a binary tree, return the inorder traversal(中序遍历) of its nodes’ values.

Example:

Input: [1,null,2,3]
   1
    \
     2
    /
   3

Output: [1,3,2]

Follow up: Recursive solution is trivial, could you do it iteratively?

Approach1

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

def inorderTraversal(root: TreeNode) -> List[int]:
    def helper(node):
        if not node:
            return []
        return helper(node.left)+[node.val]+helper(node.right)
    
    res = helper(root)
    # print(res)
    return res

Approach2

def inorderTraversal(self, root: TreeNode) -> List[int]:
    res = []
    stack = []
    cur = root
    while stack or cur:
        while cur:
            stack.append(cur)
            cur = cur.left
        top = stack.pop() #此时左子树遍历完成
        res.append(top.val)  #将父节点加入列表
        cur = top.right #遍历右子树
    return res