LeetCode day16
Diffculty: Medium
36. Valid Sudoku
Topic: Hash Table
Determine if a 9x9 Sudoku board is valid. Only the filled cells need to be validated according to the following rules:
- Each row must contain the digits 1-9 without repetition.
- Each column must contain the digits 1-9 without repetition.
- Each of the 9 3x3 sub-boxes of the grid must contain the digits 1-9 without repetition.
 A partially filled sudoku which is valid.
A partially filled sudoku which is valid.
The Sudoku board could be partially filled, where empty cells are filled with the character ‘.’.
Example 1:
Input:
[
["5","3",".",".","7",".",".",".","."],
["6",".",".","1","9","5",".",".","."],
[".","9","8",".",".",".",".","6","."],
["8",".",".",".","6",".",".",".","3"],
["4",".",".","8",".","3",".",".","1"],
["7",".",".",".","2",".",".",".","6"],
[".","6",".",".",".",".","2","8","."],
[".",".",".","4","1","9",".",".","5"],
[".",".",".",".","8",".",".","7","9"]
]
Output: trueExample 2:
Input:
[
["8","3",".",".","7",".",".",".","."],
["6",".",".","1","9","5",".",".","."],
[".","9","8",".",".",".",".","6","."],
["8",".",".",".","6",".",".",".","3"],
["4",".",".","8",".","3",".",".","1"],
["7",".",".",".","2",".",".",".","6"],
[".","6",".",".",".",".","2","8","."],
[".",".",".","4","1","9",".",".","5"],
[".",".",".",".","8",".",".","7","9"]
]
Output: false
Explanation: Same as Example 1, except with the 5 in the top left corner being
modified to 8. Since there are two 8's in the top left 3x3 sub-box, it is invalid.Note:
- A Sudoku board (partially filled) could be valid but is not necessarily solvable.
- Only the filled cells need to be validated according to the mentioned rules.
- The given board contain only digits 1-9 and the character ‘.’.
- The given board size is always 9x9
Prequisite
t = [[1,2,3],[4,5,6],[7,8,9]]
print(t) # [[1, 2, 3], [4, 5, 6], [7, 8, 9]]
print(*t) # [1, 2, 3] [4, 5, 6] [7, 8, 9]
print([i for i in zip(t)]) # [([1, 2, 3],), ([4, 5, 6],), ([7, 8, 9],)]
print(list(zip(t))) # [([1, 2, 3],), ([4, 5, 6],), ([7, 8, 9],)]
print([i for i in zip(*t)]) # [(1, 4, 7), (2, 5, 8), (3, 6, 9)]
m = ["8","3",".",".","7",".",".",".","."]
print([i for i in filter(lambda x:x != '.', m)]) # ['8', '3', '7']
print(list(filter(lambda x:x != '.', m))) # ['8', '3', '7']
s = [["8","3",".",".","7",".",".",".","."],["6",".",".","1","9","5",".",".","."], [".","9","8",".",".",".",".","6","."],["8",".",".",".","6",".",".",".","3"], ["4",".",".","8",".","3",".",".","1"], ["7",".",".",".","2",".",".",".","6"], [".","6",".",".",".",".","2","8","."], [".",".",".","4","1","9",".",".","5"], [".",".",".",".","8",".",".","7","9"]
]
for i in range(3):
for j in range(3):
tmp = [s[r][c] for r in range(i*3,i*3+3) for c in range(j*3,j*3+3)]
print(tmp)
'''
['8', '3', '.', '6', '.', '.', '.', '9', '8']
['.', '7', '.', '1', '9', '5', '.', '.', '.']
['.', '.', '.', '.', '.', '.', '.', '6', '.']
['8', '.', '.', '4', '.', '.', '7', '.', '.']
['.', '6', '.', '8', '.', '3', '.', '2', '.']
['.', '.', '3', '.', '.', '1', '.', '.', '6']
['.', '6', '.', '.', '.', '.', '.', '.', '.']
['.', '.', '.', '4', '1', '9', '.', '8', '.']
['2', '8', '.', '.', '.', '5', '.', '7', '9']
'''Approach1
def isValidSudoku(self, board: List[List[str]]) -> bool:
row = [[x for x in y if x != '.'] for y in board]
col = [[x for x in y if x != '.'] for y in zip(*board)]
pal = [[board[i+m][j+n] for m in range(3) for n in range(3) if board[i+m][j+n] != '.'] for i in (0, 3, 6) for j in (0, 3, 6)]
return all(len(set(x)) == len(x) for x in (*row, *col, *pal))Approach2
def isValidSudoku(board: List[List[str]]) -> bool:
def isvaild9(lyst):
nums = list(filter(lambda x:x != '.', lyst))
return len(set(nums)) == len(nums)
for row in board:#9行
if not isvaild9(row):
return False
for column in zip(*board):#9列
if not isvaild9(column):
return False
for row in range(3):#9块
for column in range(3):
tmp = [board[i][j] for i in range(row*3, row*3+3) for j in range(column*3, column*3+3)]
if not isvaild9(tmp):
return False
return TrueApproach3
my
def isValidSudoku(board: List[List[str]]) -> bool:
hang_dic=[[]for i in range(9)]
lie_dic=[[]for j in range(9)]#也可以构建一个9*9的列表
kuai_dic=[[]for e in range(9)]
for i in range (9):
for j in range(9):
num=board[i][j]
kuai=i//3*3+j//3
if num!='.':
num=int(num)
if num not in hang_dic[i]:
hang_dic[i].append(num)
else:
return False
if num not in lie_dic[j]:
lie_dic[j].append(num)
else:
return False
if num not in kuai_dic[kuai]:
kuai_dic[kuai].append(num)
else:
return False
return True46. Permutations
Topic: Backtracking
Given a collection of distinct integers, return all possible permutations.
Example:
Input: [1,2,3]
Output:
[
[1,2,3],
[1,3,2],
[2,1,3],
[2,3,1],
[3,1,2],
[3,2,1]
]
Approach1
my
def permute(nums: List[int]) -> List[List[int]]:
res = itertools.permutations(nums,len(nums))
return [i for i in res]Approach2
“回溯”算法也叫“回溯搜索”算法,主要用于在一个庞大的空间里搜索我们所需要的问题的解. “全排列”就是一个非常经典的“回溯”算法的应用.
执行一次深度优先遍历,从树的根结点到叶子结点形成的路径就是一个全排列:
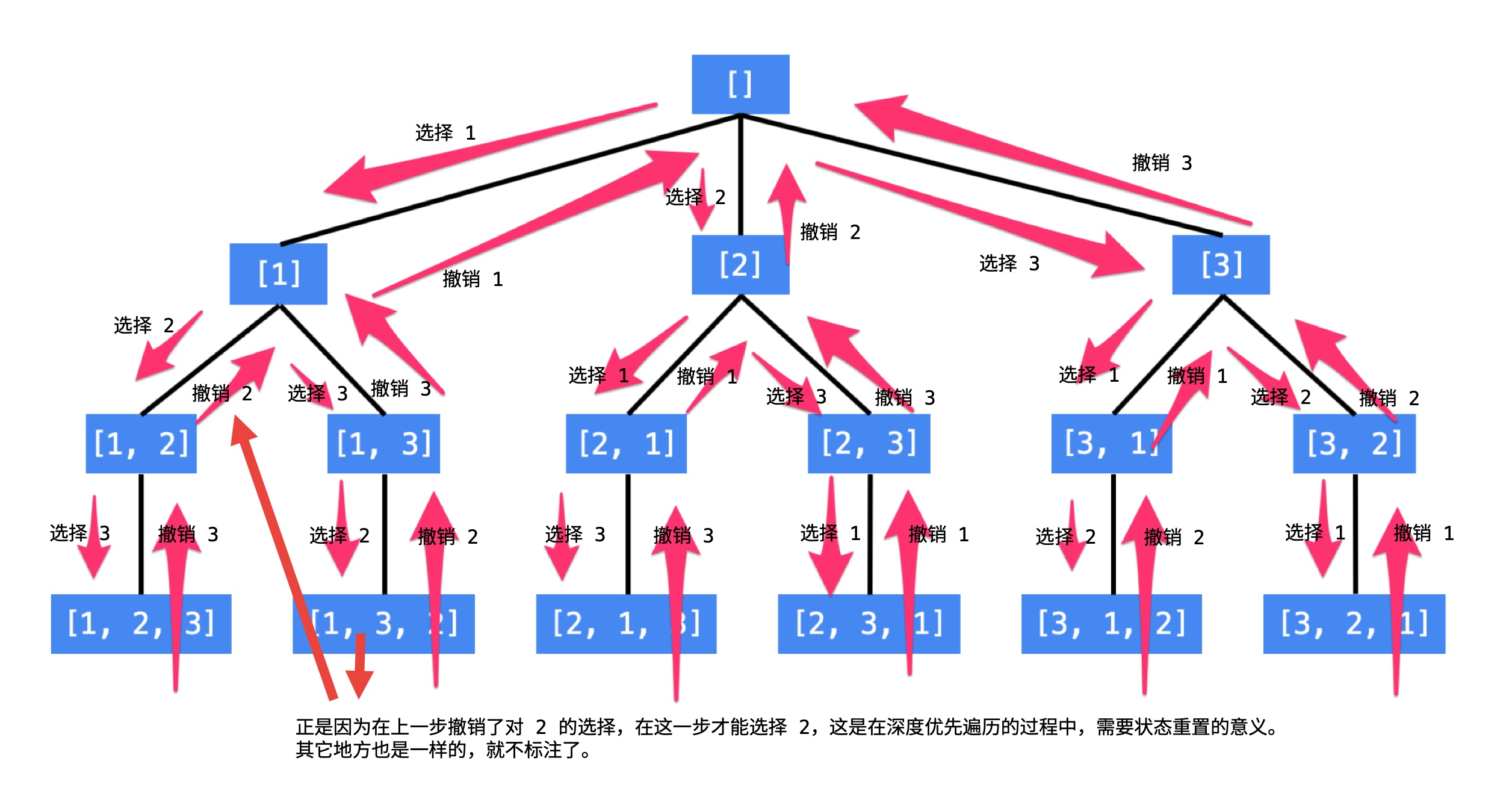
- 每一个结点表示了“全排列”问题求解的不同阶段,这些阶段通过变量的“不同的值”体现;
- 这些变量的不同的值,也称之为“状态”;
- 使用深度优先遍历有“回头”的过程,在“回头”以后,状态变量需要设置成为和先前一样;
- 因此在回到上一层结点的过程中,需要撤销上一次选择,这个操作也称之为“状态重置”;
- 深度优先遍历,可以直接借助系统栈空间,为我们保存所需要的状态变量,在编码中只需要注意遍历到相应的结点的时候,状态变量的值是正确的,具体的做法是:往下走一层的时候,path 变量在尾部追加,而往回走的时候,需要撤销上一次的选择,也是在尾部操作,因此 path 变量是一个栈。
- 深度优先遍历通过“回溯”操作,实现了全局使用一份状态变量的效果
编码:
- 首先这棵树除了根结点和叶子结点以外,每一个结点做的事情其实是一样的,即在已经选了一些数的前提,需要在剩下还没有选择的数中按照顺序依次选择一个数,这显然是一个递归结构;
- 递归的终止条件是,数已经选够了,因此需要一个变量来表示当前递归到第几层,把这个变量叫做 depth;
- 这些结点实际上表示了搜索(查找)全排列问题的不同阶段,为了区分这些不同阶段,就需要一些变量来记录为了得到一个全排列,程序进行到哪一步了,在这里需要两个变量:
- 已经选了哪些数,到叶子结点时候,这些已经选择的数就构成了一个全排列;
- 一个布尔数组 used,初始化的时候都为 false 表示这些数还没有被选择,当选定一个数的时候,就将这个数组的相应位置设置为 true ,这样在考虑下一个位置的时候,就能够以 O(1) 的时间复杂度判断这个数是否被选择过,这是一种“以空间换时间”的思想
- 把这两个变量称之为“状态变量”,它们表示了在求解一个问题的时候所处的阶段
- 在非叶子结点处,产生不同的分支,这一操作的语义是:在还未选择的数中依次选择一个元素作为下一个位置的元素,这显然得通过一个循环实现。
- 另外,因为是执行深度优先遍历,从较深层的结点返回到较浅层结点的时候,需要做“状态重置”,即“回到过去”、“恢复现场”. 例子:
- 从 [1, 2, 3] 到 [1, 3, 2] ,深度优先遍历是这样做的,从 [1, 2, 3] 回到 [1, 2] 的时候,需要撤销刚刚已经选择的数 3,因为在这一层只有一个数 3 已经尝试过了,因此程序回到上一层,需要撤销对 2 的选择,好让后面的程序知道,选择 3 了以后还能够选择 2
这种在遍历的过程中,从深层结点回到浅层结点的过程中所做的操作就叫“回溯”.
def permute(nums: List[int]) -> List[List[int]]:
if len(nums) == 0:
return []
res = []
def dfs(used, depth, path):
if depth == len(nums):
res.append(path[:])
return
else:
for i in range(len(nums)):
if not used[i]:
used[i] = True
path.append(nums[i]) # path添加一个数
dfs(used, depth + 1, path) # 再进一层
used[i] = False # 出来了, 该层的数set false
path.pop() # 出来了, path 最后添加的数pop掉
dfs([False] * len(nums), 0, [])
return res时间复杂度:O(N×N!)
空间复杂度:O(N×N!),(1)递归树深度 logN;(2)全排列个数 N!,每个全排列占空间 N. 取较大者
Approach3
上面写法会创建很多中间变量,这些中间变量很多时候是不需要的,会有一定空间和时间上的消耗.
def permute(nums: List[int]) -> List[List[int]]:
if len(nums) == 0:
return []
res = []
def dfs(state, depth, path):
if depth == len(nums):
res.append(path[:])
return
else:
for i in range(len(nums)):
if ((state >> i) & 1) == 0:
dfs(state ^ (1 << i),depth+1,path + [nums[i]])
dfs(0, 0, [])
return resApproach4
def permute(nums: List[int]) -> List[List[int]]:
if len(nums) == 0:
return []
res = []
def dfs(hash_set, depth, path):
if depth == len(nums):
res.append(path[:])
return
else:
for i in range(len(nums)):
if not nums[i] in hash_set:
hash_set.add(nums[i])
path.append(nums[i])
dfs(hash_set, depth + 1, path)
path.pop()
hash_set.remove(nums[i])
dfs(set(), 0, [])
return resdef permute(nums: List[int]) -> List[List[int]]:
if len(nums) == 0:
return []
res = []
def dfs(used, depth, path):
if depth == len(nums):
res.append(path[:])
return
else:
for i in range(len(nums)):
if ((used >> i) & 1) == 0:
used ^= (1 << i)
path.append(nums[i])
dfs(used, depth + 1, path)
used ^= (1 << i)
path.pop()
dfs(0, 0, [])
return res48. Rotate Image
Topic: Array
You are given an n x n 2D matrix representing an image.
Rotate the image by 90 degrees (clockwise).
Note:
You have to rotate the image in-place, which means you have to modify the input 2D matrix directly. DO NOT allocate another 2D matrix and do the rotation.
Example 1:
Given input matrix =
[
[1,2,3],
[4,5,6],
[7,8,9]
],
rotate the input matrix in-place such that it becomes:
[
[7,4,1],
[8,5,2],
[9,6,3]
]Example 2:
Given input matrix =
[
[ 5, 1, 9,11],
[ 2, 4, 8,10],
[13, 3, 6, 7],
[15,14,12,16]
],
rotate the input matrix in-place such that it becomes:
[
[15,13, 2, 5],
[14, 3, 4, 1],
[12, 6, 8, 9],
[16, 7,10,11]
]Approach1
def rotate(matrix: List[List[int]]) -> None:
"""
Do not return anything, modify matrix in-place instead.
先做矩阵转置(即沿着对角线翻转),然后每个列表翻转;
"""
n = len(matrix)
for i in range(n):
for j in range(i, n):
# print(matrix[i][j], matrix[j][i])
'''
1 1
2 4
3 7
5 5
6 8
9 9
'''
matrix[i][j], matrix[j][i] = matrix[j][i], matrix[i][j]
for m in matrix:
m.reverse()
def rotate2(matrix: List[List[int]]) -> None:
"""
Do not return anything, modify matrix in-place instead.
通过内置函数zip,可以简单实现矩阵转置,下面的代码等于先整体翻转,后转置;
不过这种写法的空间复杂度其实是O(n);
"""
matrix[:] = map(list, zip(*matrix[::-1]))时间复杂度:O(N^2) 空间复杂度:O(1)
49. Group Anagrams
Topic: String, Hash Table
Given an array of strings, group anagrams(颠倒字母而成的字) together.
Example:
Input: ["eat", "tea", "tan", "ate", "nat", "bat"],
Output:
[
["ate","eat","tea"],
["nat","tan"],
["bat"]
]Note:
- All inputs will be in lowercase.
The order of your output does not matter.
t = 'hat' print(sorted(t)) # ['a', 'h', 't'] print(''.join(sorted(t))) #
Approach1
def groupAnagrams(strs: List[str]) -> List[List[str]]:
res = dict()
for word in strs:
key = "".join(sorted(word))
if key in res:
res[key].append(word)
else:
res[key] = [word]
print(res) # {'aet': ['eat', 'tea', 'ate'], 'ant': ['tan', 'nat'], 'abt': ['bat']} !!
return list(res.values())
# 2. 暴力法 - 超出时间限制
# res = []
# for word in strs[:]:
# lst = []
# key = sorted(word)
# for item in strs[:]:
# if key == sorted(item):
# lst.append(item)
# strs.remove(item)
# if lst:
# res.append(lst)
# return res