LeetCode day15
Diffculty: Medium
22. Generate Parentheses
Topic: Strng, Backtracking Given n pairs of parentheses, write a function to generate all combinations of well-formed parentheses.
For example, given n = 3, a solution set is:
[
"((()))",
"(()())",
"(())()",
"()(())",
"()()()"
]
Approach1
判断回溯很简单,拿到一个问题,你感觉如果不穷举一下就没法知道答案,那就可以开始回溯了。
一般回溯的问题有三种:
- Find a path to success 有没有解
- Find all paths to success 求所有解
- 求所有解的个数
- 求所有解的具体信息
- Find the best path to success 求最优解
回溯法是一个剪枝了的二叉树。我们要得到的结果是可以 good leaf,如果不满足 good leaf 就继续向下搜索,搜索的时候需要满足一定的条件.
回溯法的代码套路是使用两个变量: res 和 path,res 表示最终的结果,path 保存已经走过的路径。如果搜到一个状态满足题目要求,就把 path 放到 res 中
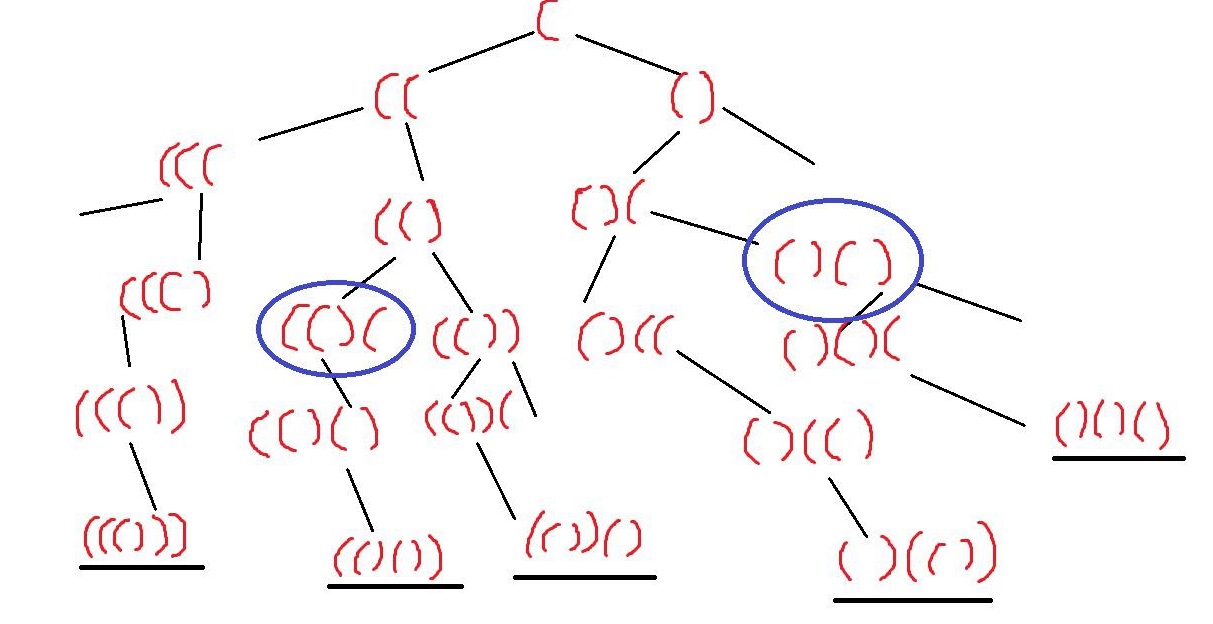
回溯, 向下搜索要满足两个条件:
- 插入数量不超过n
- 可以插入 ) 的前提是 ( 的数量大于 )
最后五条画黑线的就是最终的结果, 其中左分支都是添加左括号,右分支都是添加右括号.
def generateParenthesis(n: int) -> List[str]:
res= []
if n == 0:
return []
if n == 1:
return ['()']
def dfs(left, right, path):
if left == 0 and right == 0:
res.append(path)
return
if left > 0:
dfs(left - 1, right, path + '(')
if left < right:
dfs(left, right - 1, path + ')')
dfs(n, n, '')
return resApproach2
DP,
第 1 步:定义状态 dp[i]:使用 i 对括号能够生成的组合。(注意:每一个状态都是列表的形式)
第 2 步:状态转移方程:
- i 对括号的一个组合,在 i - 1 对括号的基础上得到,这是思考 “状态转移方程” 的基础;
- i 对括号的一个组合,一定以左括号 “(” 开始,不一定以 “)” 结尾。为此,我们可以枚举新的右括号 “)” 可能所处的位置,得到所有的组合;
- 枚举的方式就是枚举左括号 “(” 和右括号 “)” 中间可能的合法的括号对数,而剩下的合法的括号对数在与第一个左括号 “(” 配对的右括号 “)” 的后面,这就用到了以前的状态
状态转移方程是:
dp[i] = "(" + dp[可能的括号对数] + ")" + dp[剩下的括号对数]- “可能的括号对数” 与 “剩下的括号对数” 之和得为 i - 1,故 “可能的括号对数” j 可以从 0 开始,最多不能超过 i, 即 i - 1;
- “剩下的括号对数” + j = i - 1,故 “剩下的括号对数” = i - j - 1
整理得:
dp[i] = "(" + dp[j] + ")" + dp[i- j - 1] , j = 0, 1, ..., i - 1第 3 步: 思考初始状态和输出:
- 初始状态:因为我们需要 0 对括号这种状态,因此状态数组 dp 从 0 开始,0 个括号当然就是 [“”]
- 输出:dp[n]
这个方法有下面两个特点:
- 自底向上:从小规模问题开始,逐渐得到大规模问题的解集;
无后效性:后面的结果的得到,不会影响到前面的结果
def generateParenthesis(n: int) -> List[str]: if n == 0: return [] dp = [None for _ in range(n + 1)] dp[0] = [""] for i in range(1, n + 1): cur = [] for j in range(i): left = dp[j] right = dp[i - j - 1] for s1 in left: for s2 in right: cur.append("(" + s1 + ")" + s2) dp[i] = cur return dp[n]
29. Divide Two Integers
Topic: Math, Binary Search
Given two integers dividend and divisor, divide two integers without using multiplication, division and mod operator.
Return the quotient after dividing dividend by divisor.
The integer division should truncate toward zero, which means losing its fractional part. For example, truncate(8.345) = 8 and truncate(-2.7335) = -2.
Example 1:
Input: dividend = 10, divisor = 3
Output: 3
Explanation: 10/3 = truncate(3.33333..) = 3.Example 2:
Input: dividend = 7, divisor = -3
Output: -2
Explanation: 7/-3 = truncate(-2.33333..) = -2.Note:
- Both dividend and divisor will be 32-bit signed integers.
- The divisor will never be 0.
- Assume we are dealing with an environment which could only store integers within the 32-bit signed integer range: [
$−2^{31}$,$2^{31} − 1$]. For the purpose of this problem, assume that your function returns$2^{31} − 1$when the division result overflows.
Approach1
- 让被除数不断减去除数,直到不够减。每次减完后除数翻倍,并记录当前为初始除数的几倍(用 t 表示倍数 time),若发现不够减且 t 不为 1 则让除数变为原来的一半, t 也减半
- a 为被除数绝对值,b 为除数绝对值,r 表示 result,t 表示当前除数对于原始除数的倍数
- a << b 相当于 a * 2**b,a >> b 相当于 a // 2**b
异或操作 ^ 可以判断俩数字是否异号
def divide(dividend: int, divisor: int) -> int: a, b, r, t = abs(dividend), abs(divisor), 0, 1 while a >= b or t > 1: if a >= b: r += t; a -= b; t += t; b += b else: t >>= 1; b >>= 1 return min((-r, r)[dividend ^ divisor >= 0], (1 << 31) - 1)
Approach2
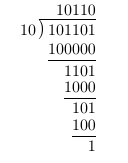
def divide(dividend: int, divisor: int) -> int:
sign = (dividend > 0) ^ (divisor > 0)
dividend = abs(dividend)
divisor = abs(divisor)
count = 0
#把除数不断左移,直到它大于被除数
while dividend >= divisor:
count += 1
divisor <<= 1
result = 0
while count > 0:
count -= 1
divisor >>= 1
if divisor <= dividend:
result += 1 << count #这里的移位运算是把二进制(第count+1位上的1)转换为十进制
dividend -= divisor
if sign: result = -result
return result if -(1<<31) <= result <= (1<<31)-1 else (1<<31)-1 33. Search in Rotated Sorted Array
Topic: Array, Binary Search
Suppose an array sorted in ascending order is rotated at some pivot unknown to you beforehand.
(i.e., [0,1,2,4,5,6,7] might become [4,5,6,7,0,1,2]).
You are given a target value to search. If found in the array return its index, otherwise return -1.
You may assume no duplicate exists in the array.
Your algorithm’s runtime complexity must be in the order of O(log n).
Example 1:
Input: nums = [4,5,6,7,0,1,2], target = 0
Output: 4Example 2:
Input: nums = [4,5,6,7,0,1,2], target = 3
Output: -1Approach1
brute force, 不是 O(log n)
def search(self, nums: List[int], target: int) -> int:
for i in range(len(nums)):
if nums[i] == target:
return i
return -1时间复杂度:O(N),这里 N 是数组的长度 空间复杂度:O(1),使用到的临时变量的个数是常数
Approach2
def search(nums: List[int], target: int) -> int:
if nums==[]:
return -1
l=0
r=len(nums)-1
while l<r:
mid=l+(r-l)//2
if nums[mid]<nums[r]:
if nums[mid]<target<=nums[r]:
l=mid+1
else:
r=mid
else:
if nums[l]<=target<=nums[mid]:
r=mid
else:
l=mid+1
if nums[l]==target:
return l
else:
return -134. Find First and Last Position of Element in Sorted Array
Topic: Array, Binary Search
Given an array of integers nums sorted in ascending order, find the starting and ending position of a given target value.
Your algorithm’s runtime complexity must be in the order of O(log n).
If the target is not found in the array, return [-1, -1].
Example 1:
Input: nums = [5,7,7,8,8,10], target = 8
Output: [3,4]Example 2:
Input: nums = [5,7,7,8,8,10], target = 6
Output: [-1,-1]Approach1
def searchRange(nums: List[int], target: int) -> List[int]:
if not nums:
return [-1, -1]
l, r = 0, len(nums)-1
# 先找起始点
while l < r:
mid = (l + r) // 2
if nums[mid] > target or nums[mid] == target:
r = mid
else:
l = mid+1
start = l
if start >= len(nums) or nums[start] != target:
return [-1, -1]
l += 1
r = len(nums)-1
# 再找终止点
while l < r:
mid = (l + r) // 2+1
if nums[mid] < target or nums[mid] == target:
l = mid
else:
r = mid-1
end = r
if nums[end] != target:
end -= 1
return [start, end]时间复杂度O(logn),空间复杂度O(1)
Approach2
def searchRange(nums: List[int], target: int) -> List[int]:
try:
start = nums.index(target)
end = len(nums) - nums[::-1].index(target) - 1
return [start,end]
except:
return [-1,-1]