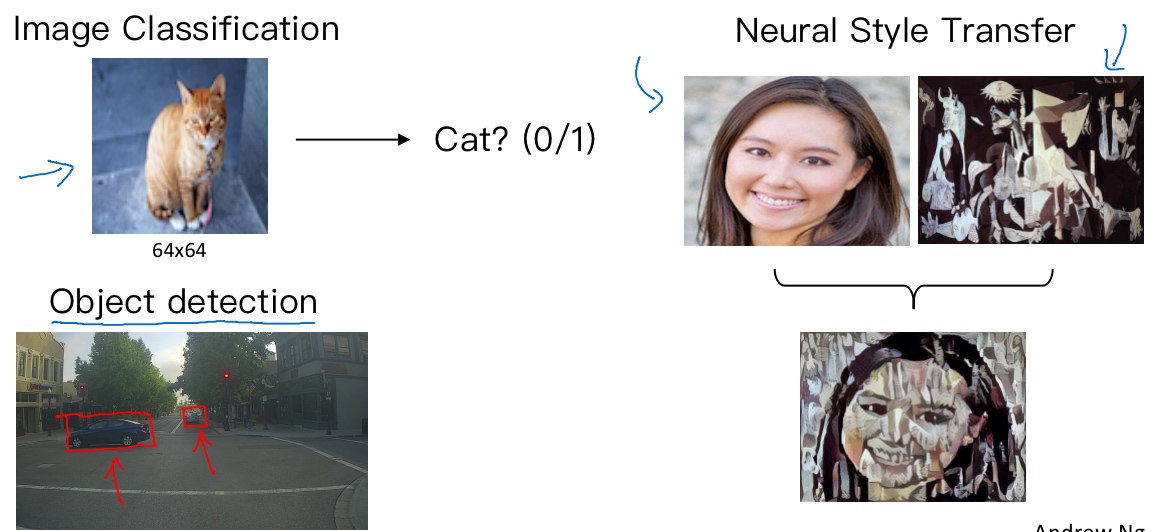
计算机视觉（Computer vision）

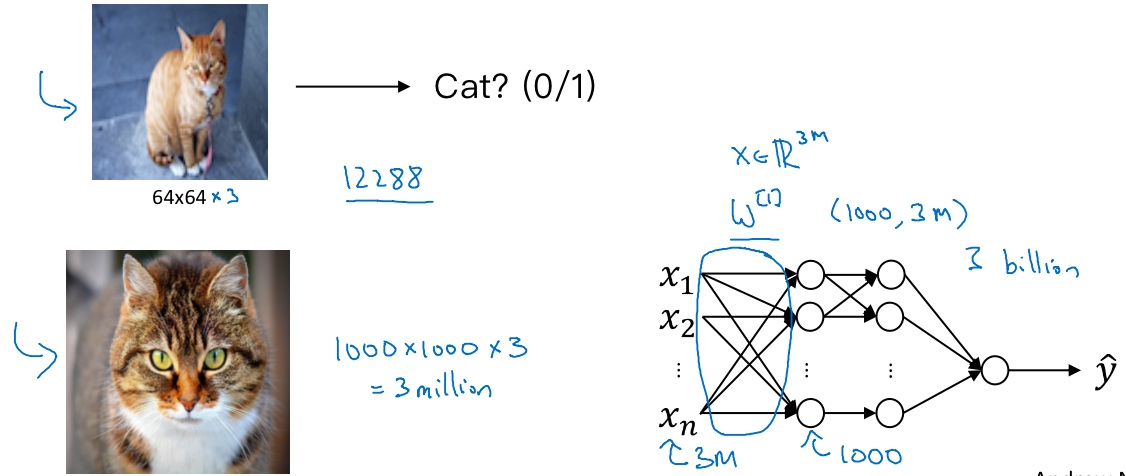
一张1000×1000的图片, 特征向量的维度达到了1000×1000×3(300万). 如果要输入300万的数据量, 在第一隐藏层中, 也许会有1000个隐藏单元，而所有的权值组成了矩阵$W^{[1]}$. 如果使用了标准的全连接网络,这个矩阵的大小将会是1000×300万, 这意味着矩阵会有30亿个参数, 这是个非常巨大的数字. 在参数如此大量的情况下, 难以获得足够的数据来防止神经网络发生过拟合和竞争需求, 要处理包含30亿参数的神经网络, 巨大的内存需求让人不太能接受.

边缘检测示例（Edge detection example）

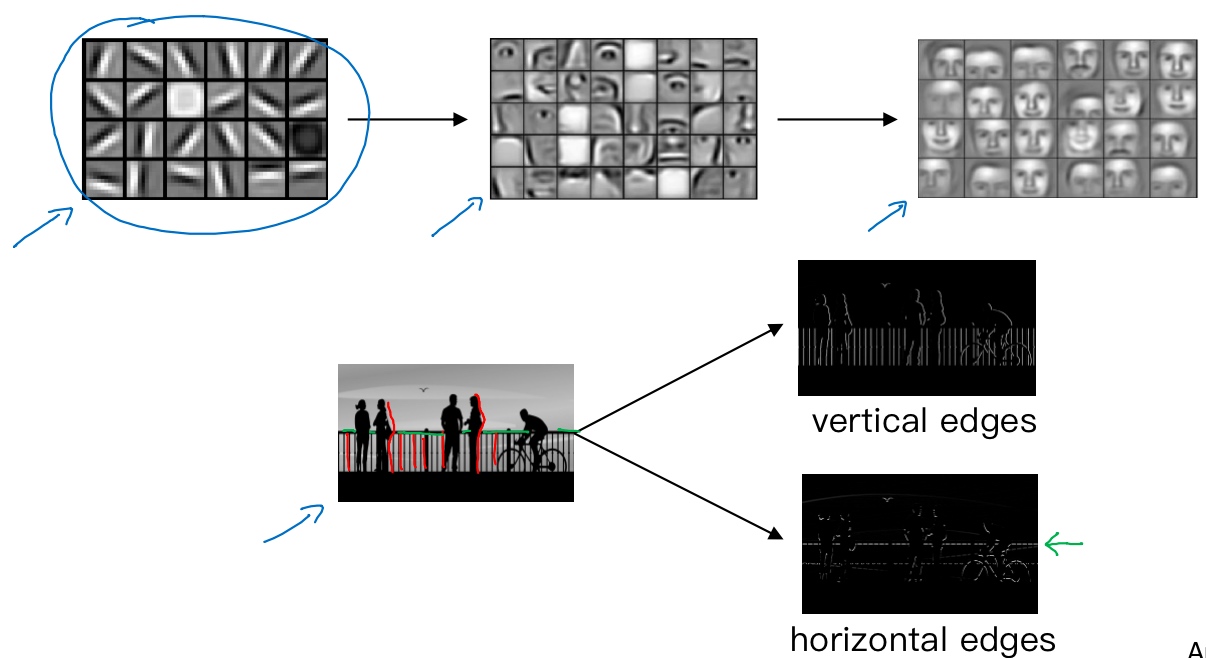
让电脑去搞清楚这张照片里有什么物体，可能做的第一件事是检测图片中的垂直边缘。比如说，在这张图片中的栏杆就对应垂直线，与此同时，这些行人的轮廓线某种程度上也是垂线。同样，你可能也想检测水平边缘，比如说这些栏杆就是很明显的水平线，它们也能被检测到

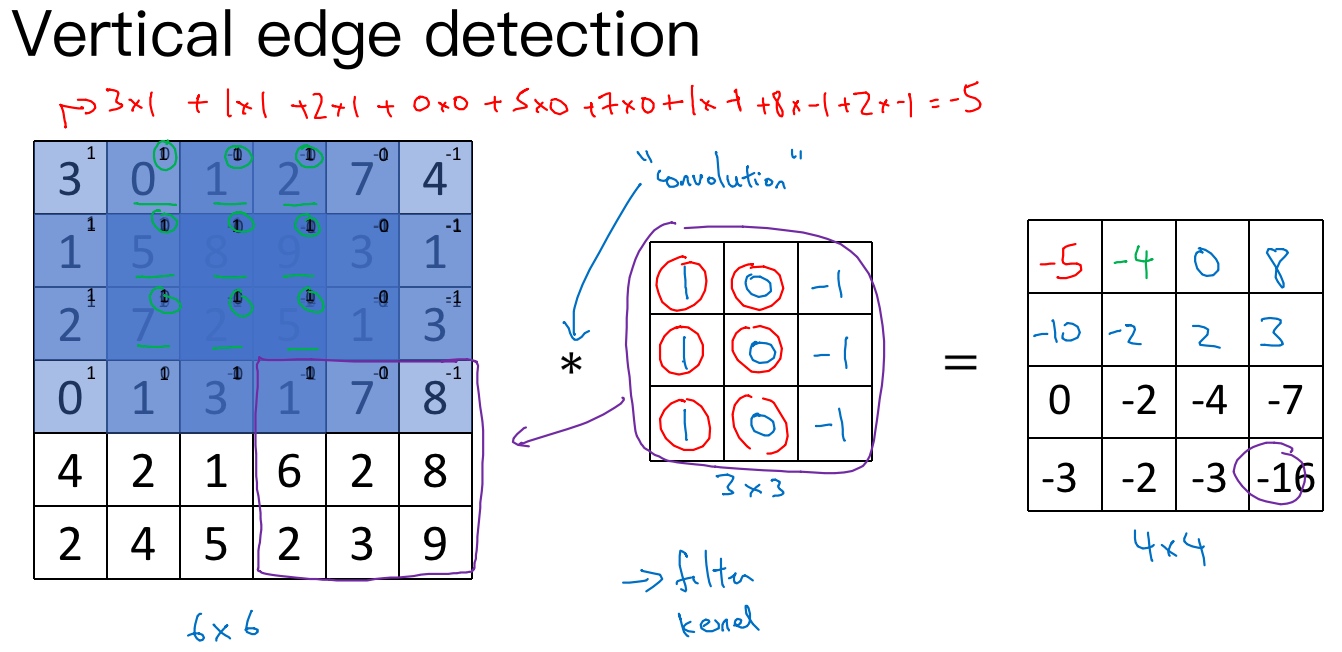
6×6的灰度图像, 6×6×1的矩阵.

‘*‘代表卷积的标准标志.

3×3的过滤器(卷积核).

然后进行元素乘法（element-wise products）运算

最后得到4×4的输出矩阵.

在tensorflow下，这个函数叫tf.conv2d;

在Keras框架下用Conv2D实现卷积运算.

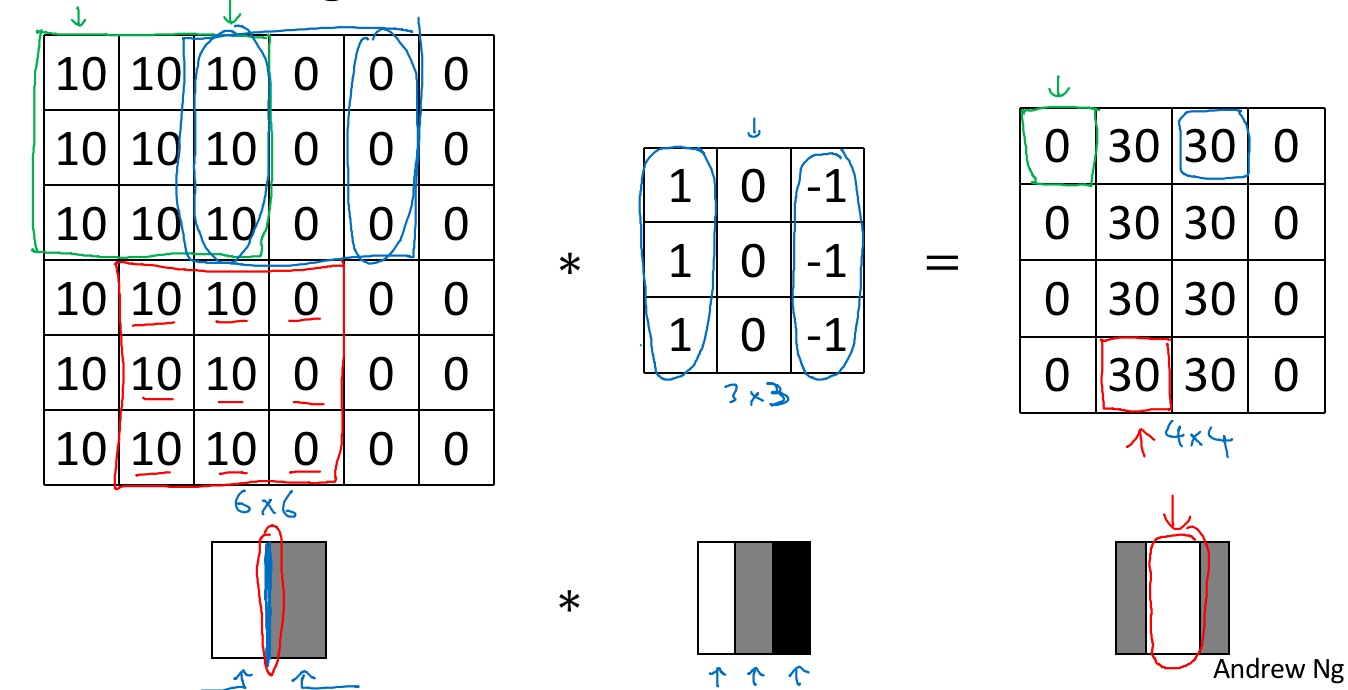
在这个例子中，在输出图像中间的亮处，表示在图像中间有一个特别明显的垂直边缘。从垂直边缘检测中可以得到的启发是，因为我们使用3×3的矩阵（过滤器），所以垂直边缘是一个3×3的区域，左边是明亮的像素，中间的并不需要考虑，右边是深色像素。在这个6×6图像的中间部分，明亮的像素在左边，深色的像素在右边，就被视为一个垂直边缘，卷积运算提供了一个方便的方法来发现图像中的垂直边缘。

更多边缘检测内容（More edge detection）

Vertical edge detection examples:

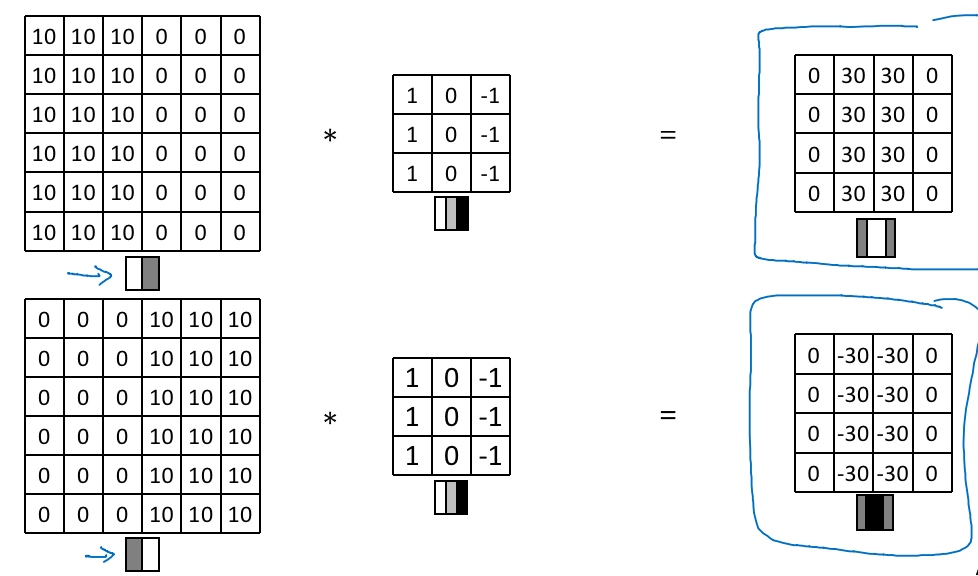
Vertical and Horizontal Edge Detection

Learning to detect edges by back propagation

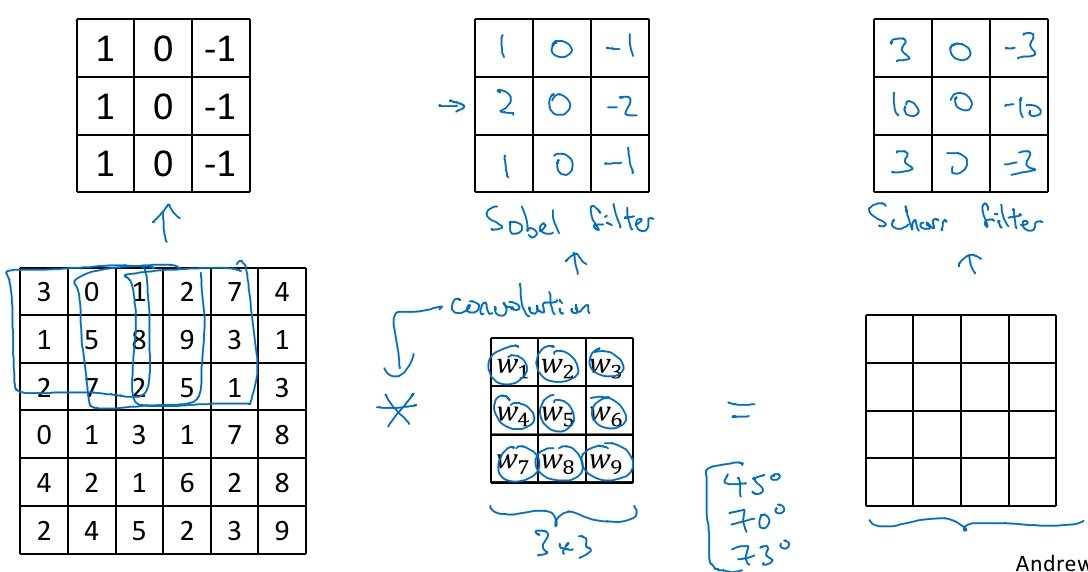
Sobel过滤器，它的优点在于增加了中间一行元素的权重，这使得结果的鲁棒性会更高一些.

Scharr过滤器，它有着和之前完全不同的特性，实际上也是一种垂直边缘检测，如果将其翻转90度，就能得到对应水平边缘检测.

将矩阵的所有数字都设置为参数，通过数据反馈，让神经网络自动去学习它们，会发现神经网络可以学习一些低级的特征，例如这些边缘的特征。不过构成这些计算的基础依然是卷积运算，使得反向传播算法能够让神经网络学习任何它所需要的3×3的过滤器，并在整幅图片上去应用它。所以这种将这9个数字当成参数的思想，已经成为计算机视觉中最为有效的思想之一.

Padding

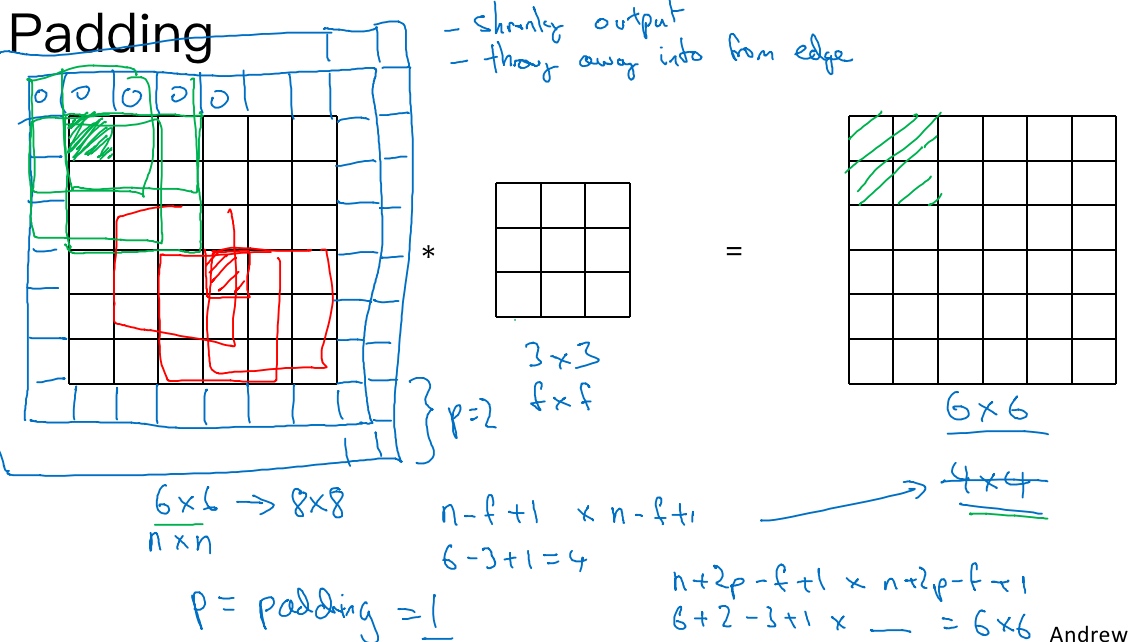
用一个3×3的过滤器卷积一个6×6的图像, 最后会得到一个4×4的输出.

所以n x n的图像, 用f x f的过滤器做卷积, 输出维度就是(n-f+1) x (n-f+1)

Drawback/Downside:

1. Every time apply a convolutional operator, the image shrinks
2. pixels on the corners/edges are used much less in the output (means throw away a lot of information neat the edge of the image)

To fix above downside – pad the image(沿着图像边缘再填充一层像素)

p = 1, 6×6的图像就被填充成了一个8×8的图像

output matrix: (n+2p-f+1) x (n+2p-f+1) which preserves the original size of the input

Valid and Same convolution

how much to pad:

‘Valid convolution’: no padding (p=0)

(n-f+1) x (n-f+1)

‘Same convolution’: 填充后, 输出大小和输入大小是一样的

(n+2p-f+1) x (n+2p-f+1)

要使得输出和输入大小相等, n+2p-f+1 = n 可以得到 p = (f-1)/2

By convention, f is usually odd(过滤器的维数通常是奇数), 原因:

1. 如果是一个偶数，那么只能使用一些不对称填充

2. 当有一个奇数维过滤器，比如3×3或者5×5的，它就有一个中心点, 便于指出过滤器的位置

卷积步长（Strided convolutions）

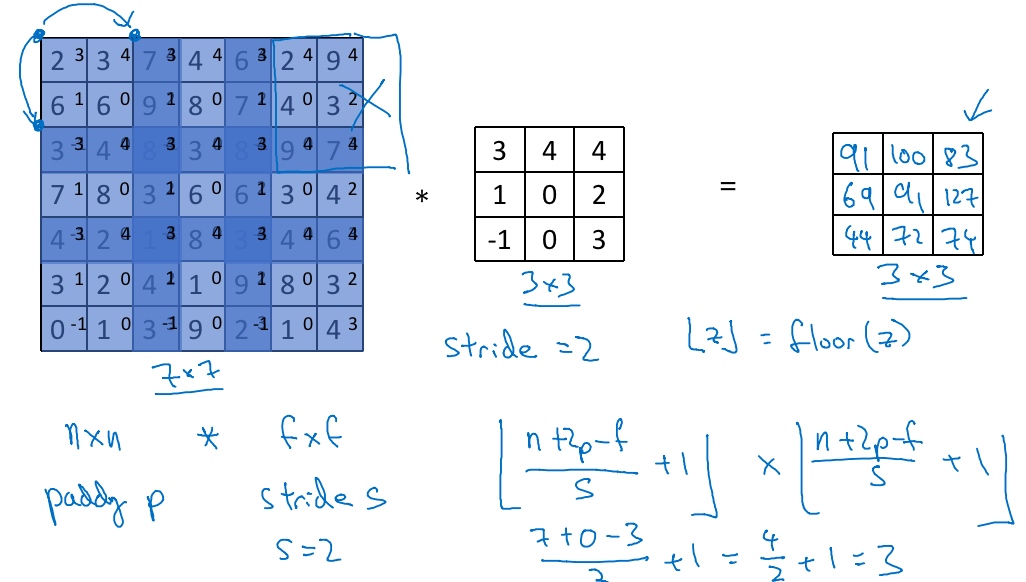
用一个f x f的过滤器卷积一个n x n的图像，padding为p，步幅stride为s, 输出:

$\lfloor \frac{n+2p-f}{s}+1 \rfloor * \lfloor \frac{n+2p-f}{s}+1 \rfloor$, $\lfloor\rfloor$是向下取整的意思

Technical note on cross-correlation(互相关) vs. convolution:

• Convolution in math textbook 卷积在数学中, 过滤器要先做一个垂直和水平的翻转, 才开始做卷积操作
• 前面使用的操作，有时被称为互相关（cross-correlation）而不是卷积（convolution）。但在深度学习文献中，按照惯例，将这（不进行翻转操作）叫做卷积操作。

三维卷积（Convolutions over volumes）

Convolutions on RGB images:

彩色图像的维度是6×6×3, 第一个6代表图像高度，第二个6代表宽度，这个3代表通道的数目.

跟一个三维的过滤器，它的维度是3×3×3，这样这个过滤器也有三层，对应红绿、蓝三个通道.

图像的通道数必须和过滤器的通道数匹配

输出会是一个4×4的图像(注意是4×4×1)

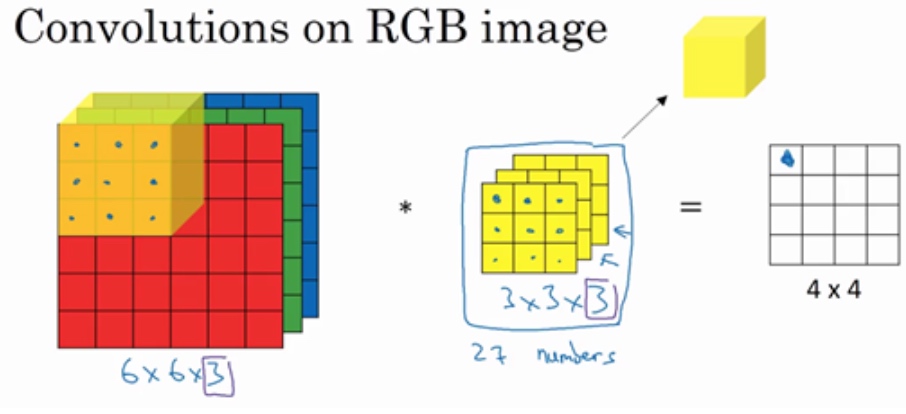
3×3×3的过滤器有27个数, 依次取这27个数，然后乘以相应的红绿蓝通道中的数字, 然后把这些数都加起来，就得到了输出的第一个数字.

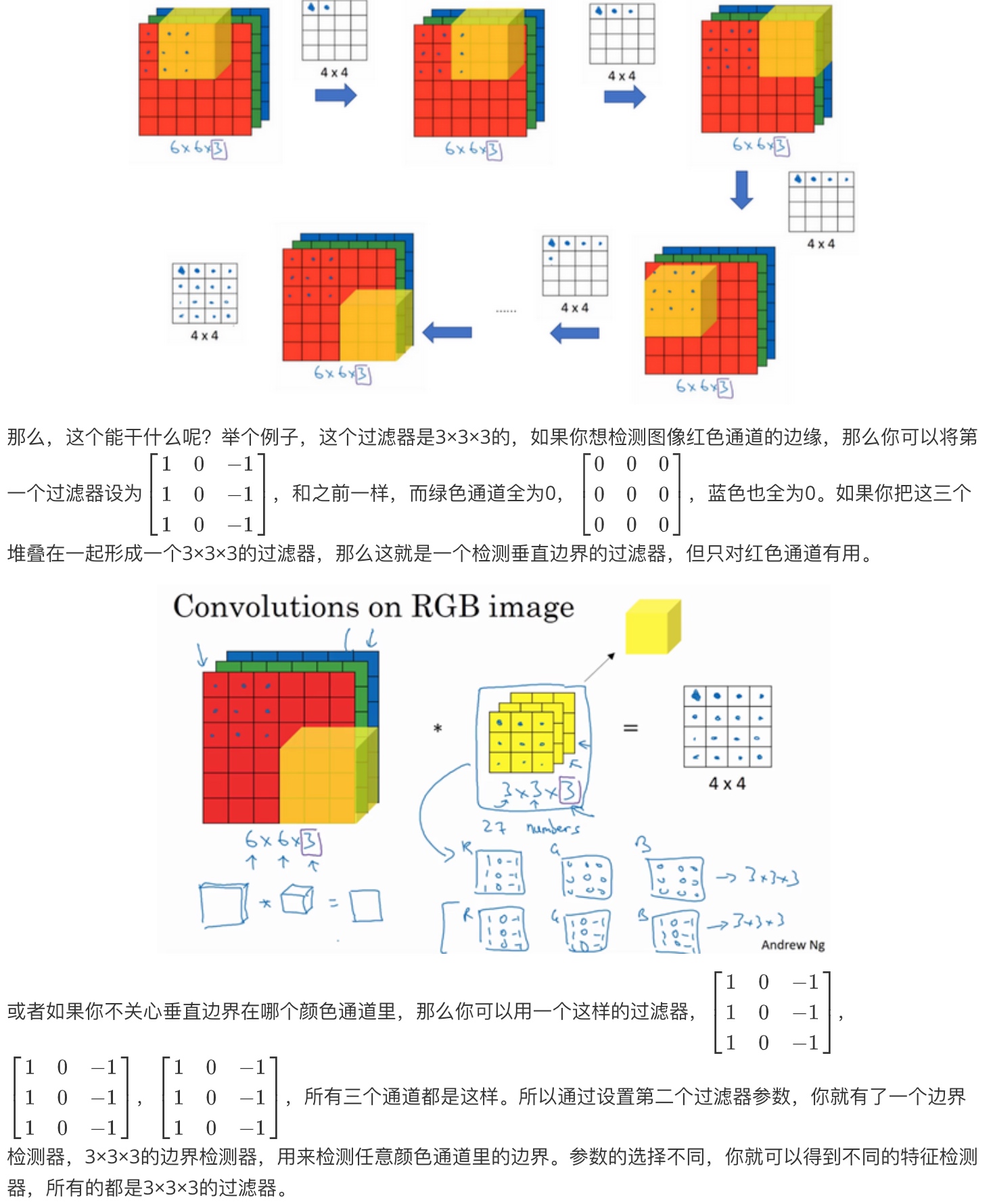
Multiple filters(同时用多个过滤器):

6×6×3的图像和这个3×3×3的过滤器卷积，得到4×4的输出. 假设第一个过滤器(黄色)是一个垂直边界检测器, 第二个过滤器(橘色)是一个水平边缘检测器.

所以和第一个过滤器卷积，可以得到第一个4×4的输出，然后卷积第二个过滤器，得到一个不同的4×4的输出. 做完卷积后, 把这两个输出堆叠在一起，这样就得到了一个4×4×2的输出立方体, 所以这就是一个4×4×2的输出立方体, 这里的2来源于用了两个不同的过滤器.

Summary:

有n x n x n_c(通道数)的输入图像, 卷积上一个f x f x n_c, 得到(n-f+1) x (n-f+1) x n_c^ , n_c^ 就是下一层的通道数(用的过滤器的个数)

对立方体做卷积的概念, 使得可以在三个通道的RGB图像上进行操作, 可以检测2个特征，比如垂直和水平边缘或者10个或者128个或者几百个不同的特征，并且输出的通道数会等于要检测的特征数.

单层卷积网络（One layer of a convolutional network）

构建卷积神经网络的卷积层:

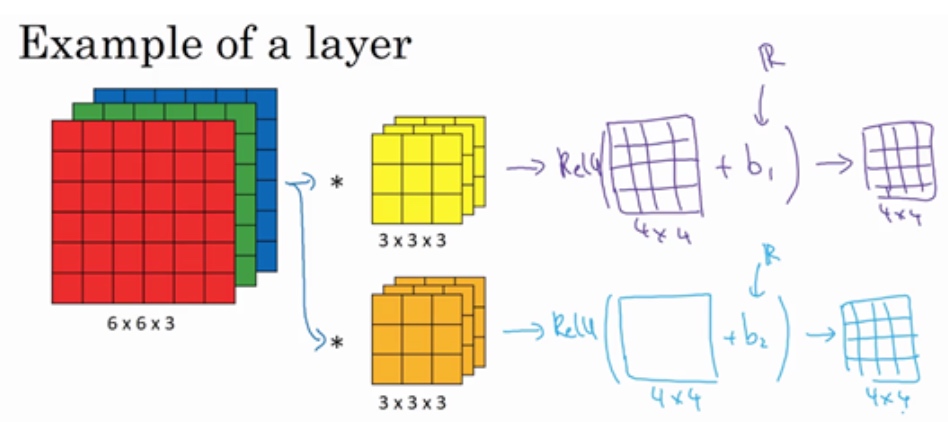
假设使用第一个过滤器进行卷积，得到第一个4×4矩阵. 然后增加偏差(实数), 应用非线性函数(E.g.ReLU), 输出结果是一个4x4矩阵. 第二个过滤器同理, 最终两个矩阵叠加, 得到一个4x4x2的矩阵.

前向传播的操作:

1. $z^{[1]}=W^{[1]}a^{[0]}+b^{[1]}$
2. $a^{[1]} = g(z^{[1]})$

其中, $a^{[0]}=x$相当于6x6x3的输入, $W^{[1]}$相当于两个3x3x3过滤器

运用线性函数$W^{[1]}a^{[0]}$再加上偏差$b^{[1]}$，然后应用激活函数ReLU. 这样就通过神经网络的一层把一个6×6×3的维度$a^{[0]}$演化为一个4×4×2维度的$a^{[1]}$，这就是卷积神经网络的一层.

Number of parameters in one layer

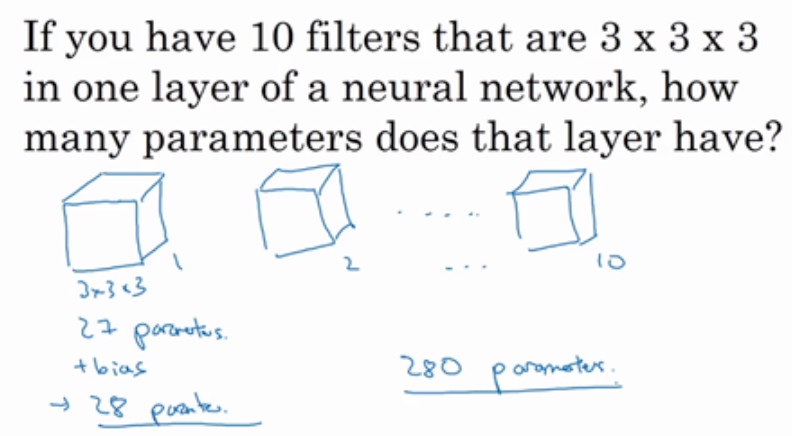
每个过滤器有27个参数, 也就是27个数. 然后加上一个偏差b, 总的参数一个28个. 所以10个过滤器就是28x10, 也就是280个参数

不论输入图片有多大, 参数始终都是280个. 用这10个过滤器来提取特征，如垂直边缘，水平边缘和其它特征. 即使这些图片很大，参数却很少，这就是卷积神经网络的一个特征，叫作“避免过拟合”.

卷积层中,

$f^{[l]}$表示过滤器的大小 $f \times f$

$p^{[l]}$表示padding的数量

$s^{[l]}$表示stride

$n^{[l]}_c$表示过滤器数量

输入: $n^{[l-1]}_H \times n^{[l-1]}_W \times n_c^{[l-1]}$, 其中$n_c^{[l-1]}$表示上一层的颜色通道数

输出: $n^{[l]}_H \times n^{[l]}_W \times n_c^{[l]}$, 其中$n_c^{[l]}$表示过滤器的数量, l层输出图像的高度为$n^{[l]}_H = \lfloor \frac{n^{[l-1]}_H+2p^{[l]}-f^{[l]}}{s^{[l]}} +1 \rfloor$, 同理, 宽度为$n^{[l]}_W = \lfloor \frac{n^{[l-1]}_W+2p^{[l]}-f^{[l]}}{s^{[l]}} +1 \rfloor$

• 每个过滤器的维度: $f^{[l]} \times f^{[l]} \times n^{[l-1]}_c$ (过滤器中通道的数量必须与输入中通道的数量一致)

• 激活值$a^{[l]}$的维度: $n^{[l]}_H \times n^{[l]}_W \times n_c^{[l]}$, 当执行批量梯度下降时，如果有m个例子，就是有m个激活值的集合，那么输出$A^{[l]}: m \times n^{[l]}_H \times n^{[l]}_W \times n_c^{[l]}$

• 权重参数(参数W)的维度: $f^{[l]} \times f^{[l]} \times n_c^{[l-1]} \times n_c^{[l]}$. 权重就是所有过滤器的集合(一个过滤器的维度$f^{[l]} \times f^{[l]} \times n_c^{[l-1]}$)再乘以过滤器的总数量($n_c^{[l]}$)

• 偏差参数的维度: 每个过滤器都有一个偏差参数，它是一个实数, $1 \times 1 \times 1 \times n_c^{[l]}$

简单卷积网络示例（A simple convolution network example）

图片大小是39×39×3, 0层的通道数为3 ($n_c^{[0]}=3$).

假设第一层用一个3×3的过滤器来提取特征，那么$f^{[1]}=3$. $s^{[1]}=1, p^{[1]}=0$, 如果有10个过滤器, 神经网络下一层的激活值的维度为37x37x10 ($\frac{39+0-3}{1}+1=37$)

其他几层同理, 最终为图片提取了7×7×40个特征, 计算出来就是1960个特征, 将其平滑或展开成1960个单元. 平滑处理后可以输出一个向量，其填充内容是logistic回归单元还是softmax回归单元, 用$\tilde{y}$表示最终神经网络的预测输出

随着神经网络计算深度不断加深，通常开始时的图像也要更大一些，初始值为39×39，高度和宽度会在一段时间内保持一致，然后随着网络深度的加深而逐渐减小，从39到37，再到17，最后到7. 而通道数量在增加，从3到10，再到20，最后到40. 许多其它卷积神经网络中，也可以看到这种趋势.

Types of layer in a convolutional network:

• Convolution (CONV) 卷积层
• Pooling (POOL) 池化层
• Fully connected (FC) 全连接层

池化层（Pooling layers）

卷积网络也经常使用池化层来缩减模型的大小，提高计算速度，同时提高所提取特征的鲁棒性

Max Pooling:

左上区域的最大值是9，右上区域的最大元素值是2，左下区域的最大值是6，右下区域的最大值是3. 为了计算出右侧这4个元素值，需要对输入矩阵的2×2区域做最大值运算.

Hyperparameter:

f = 2

s = 2

可以把这个4×4区域看作是某些特征的集合，也就是神经网络中某一层的非激活值集合, 数字大意味着可能探测到了某些特定的特征.

最大化运算的实际作用就是，如果在过滤器中提取到某个特征，那么保留其最大值. 如果没有提取到这个特征，可能在象限(quadrants)中不存在这个特征，那么其中的最大值也还是很小.

其中一个有意思的特点就是，它有一组超参数，但并没有参数需要学习。实际上，梯度下降没有什么可学的，一旦确定了f和s，它就是一个固定运算，梯度下降无需改变任何值.

另一个示例:

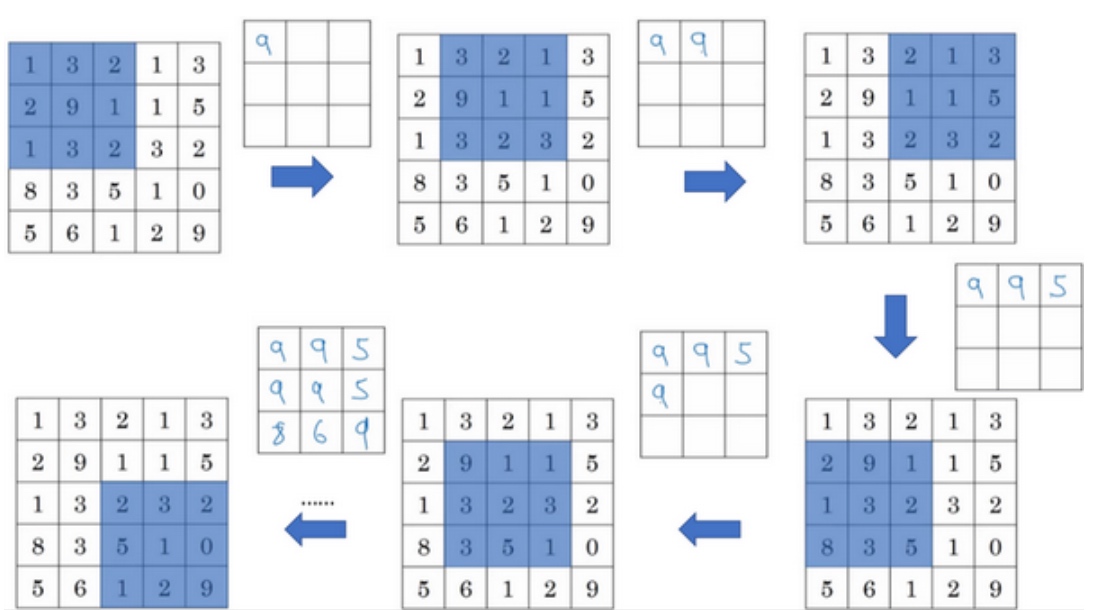
输入是一个5×5的矩阵, 采用最大池化法, 它的过滤器参数为3×3 (即f=3), s=1. 如果输入是三维的，那么输出也是三维的。例如，输入是5×5×2，那么输出是3×3×2.

Average Pooling:

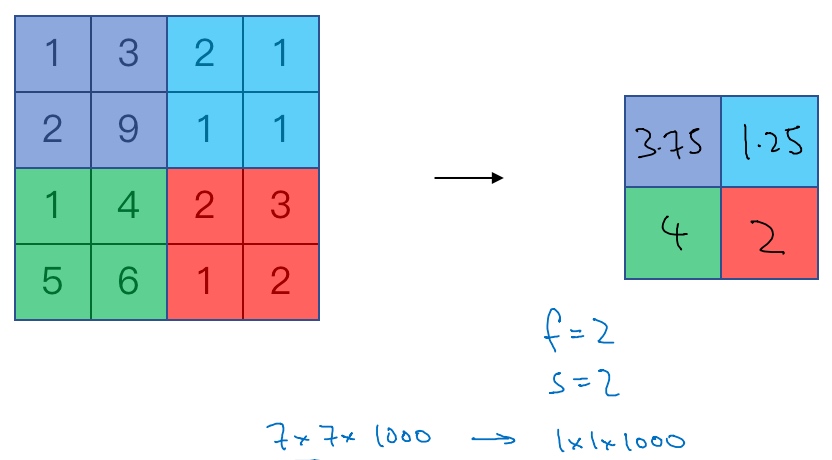
目前来说，最大池化比平均池化更常用. 但也有例外，就是深度很深的神经网络，可以用平均池化来分解规模为7×7×1000的网络的表示层，在整个空间内求平均值，得到1×1×1000.

Summary:

池化的超级参数包括过滤器大小f和步幅s，常用的参数值为f=2,s=2, 应用频率非常高, 其效果相当于高度和宽度缩减一半. 最大池化很少用padding.

最大池化的输入就是$n_H \times n_w \times n_c$. 假设没有padding，则输出为$\lfloor \frac{n_H-f}{s}+1 \rfloor \times \frac{n_W-f}{s}+1 \rfloor \times n_c$. 输入通道与输出通道个数相同，因为对每个通道都做了池化.

注意: 池化过程中没有需要学习的参数。执行反向传播时，反向传播没有参数适用于最大池化。只有这些设置过的超参数，可能是手动设置的，也可能是通过交叉验证设置的

卷积神经网络示例（Convolutional neural network example）

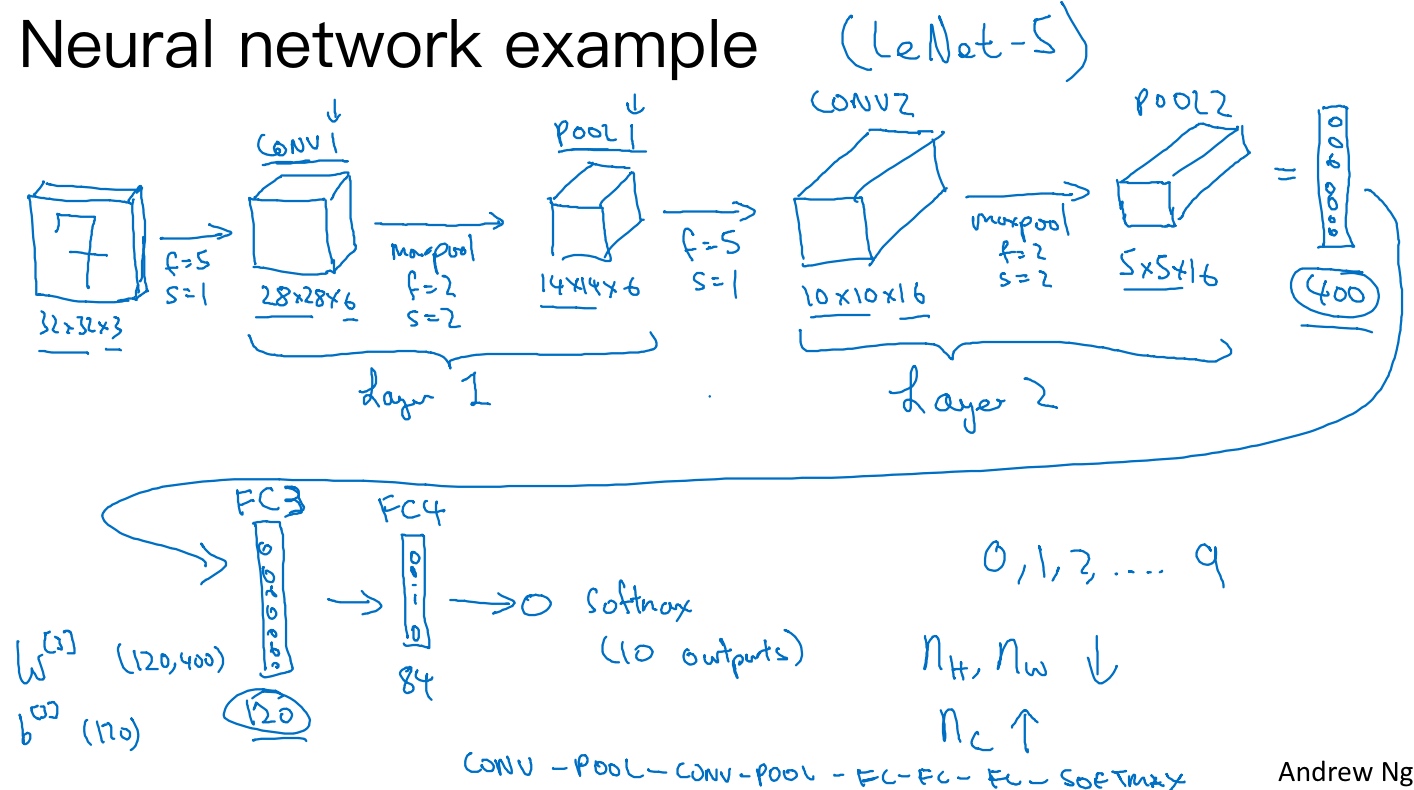
假设有一张大小为32×32×3的输入图片(RGB模式的图片), 想做手写体数字识别. 这个网络模型和经典网络LeNet-5非常相似.

1. 输入是32×32×3的矩阵，假设第一层使用过滤器大小为5×5，步幅是1，padding是0，过滤器个数为6，那么输出为(32-5+1)28×28×6。将这层标记为CONV1，它用了6个过滤器，增加了偏差，应用了非线性函数，可能是ReLU非线性函数，最后输出CONV1的结果。
2. 然后构建一个池化层，这里我选择用最大池化，参数f=2，s=2，padding=0. 最大池化使用的过滤器为2×2，步幅为2，表示层的高度和宽度会减少一半。因此，28×28变成了14×14，通道数量保持不变，所以最终输出为14×14×6，将该输出标记为POOL1。
3. 再为它构建一个卷积层，过滤器大小为5×5，步幅为1，这次我们用16个过滤器，最后输出一个(14-5+1)10×10×16的矩阵，标记为CONV2.
4. 做最大池化，超参数f=2，s=2, 高度和宽度会减半，最后输出为5×5×16，标记为POOL2，这就是神经网络的第二个卷积层，即Layer2
5. 5×5×16矩阵包含400个元素，现在将POOL2平整化为一个大小为400的一维向量, 然后利用这400个单元构建下一层
6. 下一层含有120个单元，这就是第一个全连接层，标记为FC3, 它的权重矩阵为$W^{[3]}$，维度为120×400.(所谓的“全连接”，就是这400个单元与这120个单元的每一项连接), 还有一个偏差参数b, 维度为120x1.
7. 对这个120个单元再添加一个全连接层，这层更小，假设它含有84个单元，标记为FC4
8. 最后，用这84个单元填充一个softmax单元。要通过手写数字识别来识别手写0-9这10个数字，这个softmax就会有10个输出

在卷积神经网络文献中, 会把CONV1和POOL1共同作为一个卷积，并标记为Layer1. (人们在计算神经网络有多少层时，通常只统计具有权重和参数的层 (池化层没有权重和参数，只有一些超参数)).

随着神经网络深度的加深，高度和宽度通常都会减少，前面我就提到过，从32×32到28×28，到14×14，到10×10，再到5×5。所以随着层数增加，高度和宽度都会减小，而通道数量会增加，从3到6到16不断增加，然后得到一个全连接层.

在神经网络中，另一种常见模式就是一个或多个卷积后面跟随一个池化层，然后一个或多个卷积层后面再跟一个池化层，然后是几个全连接层，最后是一个softmax。这是神经网络的另一种常见模式.

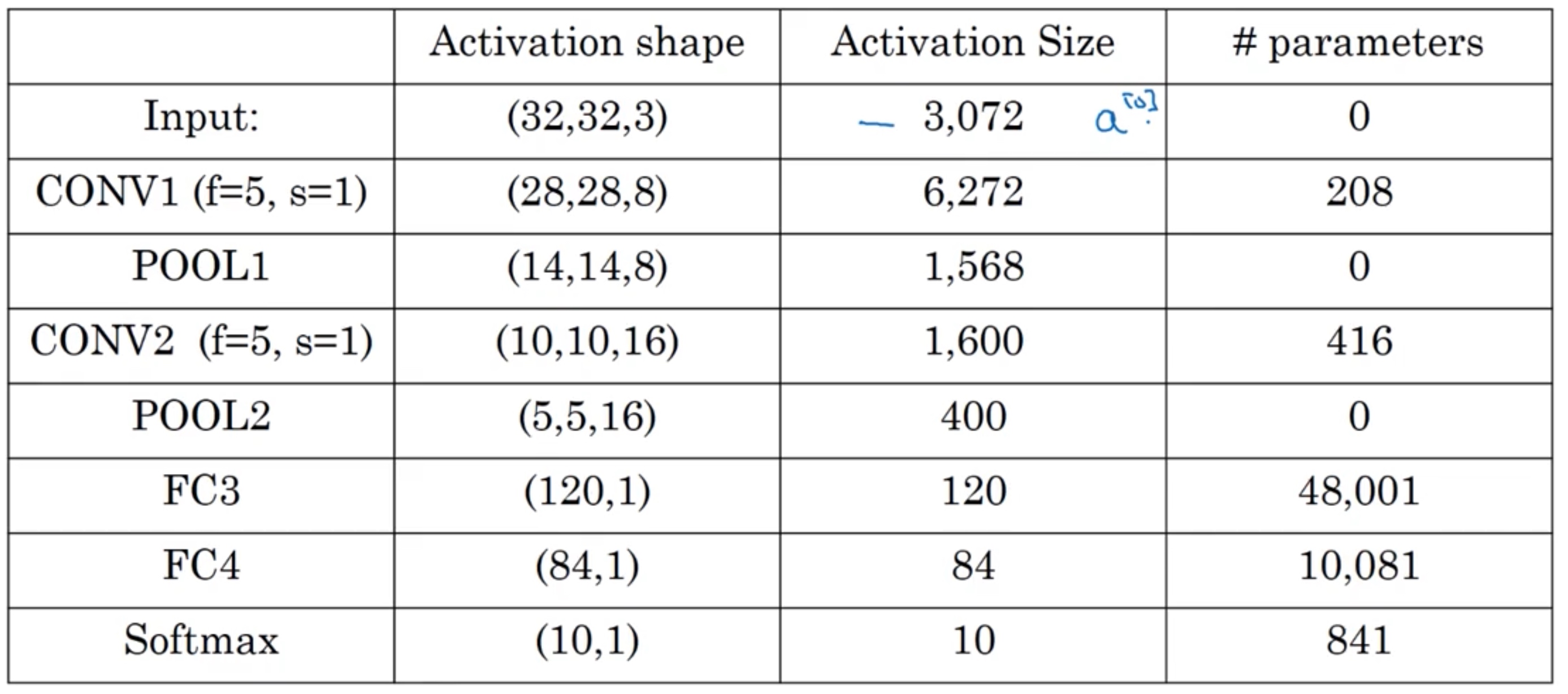
有几点要注意，第一，池化层和最大池化层没有参数；第二卷积层的参数相对较少，其实许多参数都存在于神经网络的全连接层。观察可发现，随着神经网络的加深，激活值尺寸会逐渐变小，如果激活值尺寸下降太快，也会影响神经网络性能。示例中，激活值尺寸在第一层为6000，然后减少到1600，慢慢减少到84，最后输出softmax结果

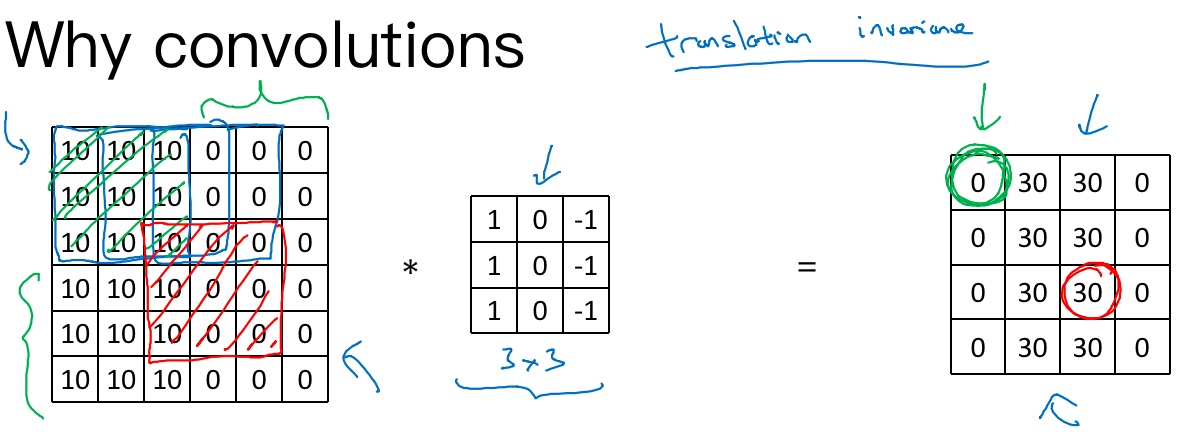
为什么使用卷积？（Why convolutions?）

假设有一张32×32×3维度的图片, 用了6个大小为5×5的过滤器，输出维度为28×28×6. 32×32×3=3072，28×28×6=4704, 构建一个神经网络，其中一层含有3072个单元，下一层含有4074个单元，两层中的每个神经元彼此相连，然后计算权重矩阵，它等于4074×3072≈1400万，所以要训练的参数很多。虽然以现在的技术，可以用1400多万个参数来训练网络，因为这张32×32×3的图片非常小，训练这么多参数没有问题。如果这是一张1000×1000的图片，权重矩阵会变得非常大。

而这个卷积层的参数数量，每个过滤器都是5×5，一个过滤器有25个参数，再加上偏差参数，那么每个过滤器就有26个参数，一共有6个过滤器，所以参数共计156个，参数数量还是很少.

The reason that a ConvNet has small parameters(卷积网络映射这么少参数有两个原因):

1. Parameter sharing
   • feature detector (such as a vertical edge detector) that’s useful in one part of the image is probably useful in another part of the image
2. Sparsity of connections
   • In each layer, each output value depends only on a small number of inputs. (任意一个输出单元(例如绿色圈住的0)仅与36个输入特征中9个相连接(绿色线划掉部分), 而且其它像素值都不会对输出产生任影响，这就是稀疏连接的概念)

神经网络可以通过这两种机制减少参数，以便我们用更小的训练集来训练它，从而预防过度拟合

Putting it together

最后，我们把这些层整合起来，看看如何训练这些网络。比如我们要构建一个猫咪检测器，有个标记训练集，x表示一张图片，$\tilde{y}$是二进制标记或某个重要标记。我们选定了一个卷积神经网络，输入图片，增加卷积层和池化层，然后添加全连接层，最后输出一个softmax，即$\tilde{y}$。卷积层和全连接层有不同的参数w和偏差b，我们可以用任何参数集合来定义代价函数，并随机初始化其参数w和b，代价函数J等于神经网络对整个训练集的预测的损失总和再除以m（即$Cost J = \frac{1}{m}\sum_{i=1}^m L(\tilde{y}^{(i)},y^{(i)})$）.所以训练神经网络，你要做的就是使用梯度下降法，或其它算法，例如Momentum梯度下降法，含RMSProp或其它因子的梯度下降来优化神经网络中所有参数，以减少代价函数J的值。通过上述操作你可以构建一个高效的猫咪检测器或其它检测器.