6. Hyperparameter tuning
调试处理(Tuning process)
系统地组织超参调试过程
目前所学的超参数(按重要性排序):
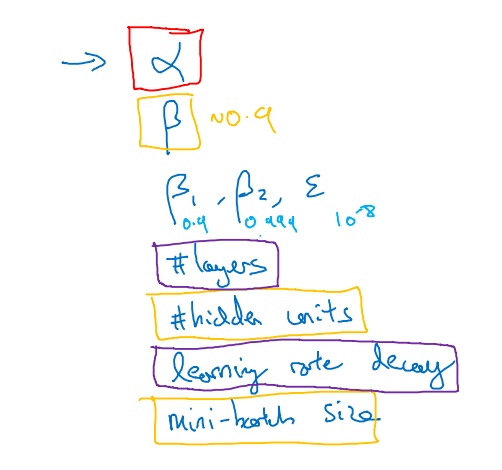
$\alpha$$\beta$- # hidden units
- mini-batch size
- # layers
- learning rate decay
$\beta_1,\beta_2, \epsilon$(use default value, 0.9, 0.999, 10^(-8))
选择调式值:
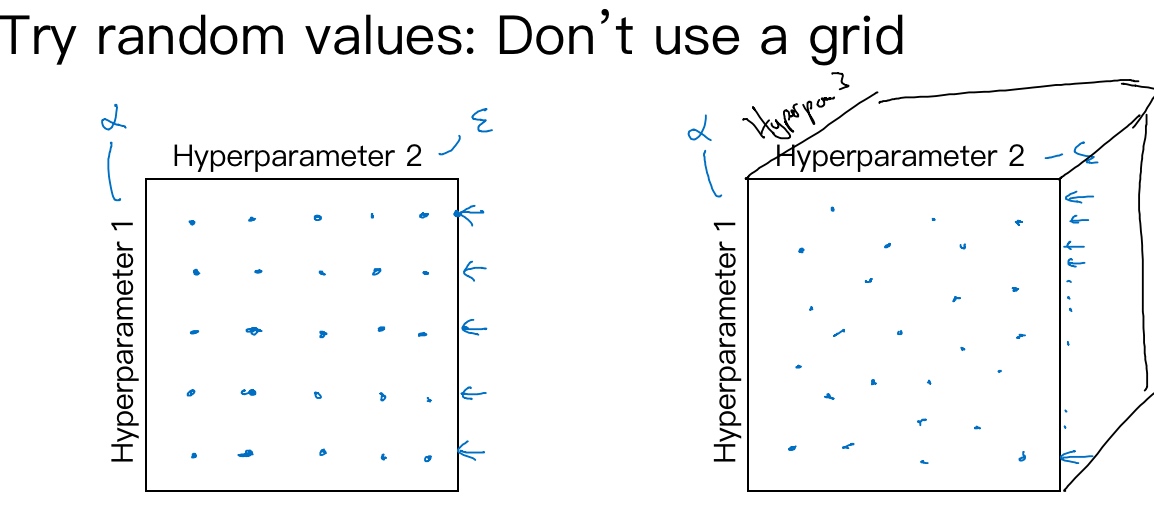
不要尝试在网格中取点, 而是随机选择点. 在左图上, 一共25个模型, 但进行试验的hyperparameter1 只有5个. 相对于随机取值(右图), 会试验25个独立的heperparameter1.
采用由粗糙到精细的策略:

比如在上图网格中随机取值, 发现效果最好的某个点, 并且该点周围的点效果也好, 那么接下来要做的就是放大那块下区域(小蓝色方框), 然后在其中更密集得取值或随机取值, 这种从粗到细的搜索也经常使用.
为超参数选择合适的范围(Using an appropriate scale to pick hyperparameters)
假设要选取隐藏单元的数量$n^{[l]}$, 选取的取值范围是从50到100中某点, 可以做一条50-100的数轴并随机的在其取点, 这是一个搜索特定超参数的很直观的方式. 选取隐藏层也可这么做.
但是有些参数并不适用. 例如学习率$\alpha$, 怀疑其值最小是0.0001或最大是1. 如果画一条从0.0001到1的数轴, 沿其随机均匀取值, 90%的数值将会落在0.1到1之间, 而在0.0001到0.1之间只有10%的搜索资源,这看上去不太对.

用对数标尺搜索超参数的方式会更合理. 分别依次取0.0001,0.001,0.01,0.1,1,在对数轴上均匀随机取点.
在python中, r=-4*np.random.rand(), 然后$\alpha$随机取值, $\alpha = 10^r \Rightarrow r \in [4,0]\Rightarrow \alpha \in [10^{-4}10^0]$,
总结一下,在对数坐标下取值,取最小值的对数就得到a的值,取最大值的对数就得到b值,所以现在你在对数轴上的10^a 到10^b 区间取值,在a,b间随意均匀的选取r值,将超参数设置为10^r ,这就是在对数轴上取值的过程.

If you think β (hyperparameter for momentum) is between on 0.9 and 0.99, which of the following is the recommended way to sample a value for beta?
r = np.random.rand()
beta = 1-10**(- r - 1)
超参数调试的实践:Pandas VS Caviar(Hyperparameters tuning in practice: Pandas vs. Caviar)
Intuitions do get stale. Re-evaluate occasionally. (建议至少每隔几个月一次, 重新测试或评估你的超参数, 以确保你对数值依然很满意)

这两种方式的选择,是由你拥有的计算资源决定的,如果你拥有足够的计算机去平行试验许多模型,那绝对采用鱼子酱方式,尝试许多不同的超参数, 同一时间训练多个模型.
归一化网络的激活函数(Normalizing activations in a network)
归一化:1)把数据变成(0,1)或者(1,1)之间的小数。主要是为了数据处理方便提出来的,把数据映射到0~1范围之内处理,更加便捷快速。2)把有量纲表达式变成无量纲表达式(成为纯量),便于不同单位或量级的指标能够进行比较和加权. (无量纲:通过某种方法能去掉实际过程中的单位,从而简化计算)
标准化:在机器学习中,可能要处理不同种类的资料,例如,音讯和图片上的像素值,这些资料可能是高维度的,资料标准化后会使每个特征中的数值平均变为0(将每个特征的值都减掉原始资料中该特征的平均)、标准差变为1,这个方法被广泛的使用在许多机器学习算法中(例如:支持向量机、逻辑回归和类神经网络)。
中心化:平均值为0,对标准差无要求 归一化和标准化的区别:归一化是将样本的特征值转换到同一量纲下把数据映射到[0,1]或者[-1, 1]区间内,仅由变量的极值决定,因区间放缩法是归一化的一种。标准化是依照特征矩阵的列处理数据,其通过求z-score的方法,转换为标准正态分布,和整体样本分布相关,每个样本点都能对标准化产生影响。它们的相同点在于都能取消由于量纲不同引起的误差;都是一种线性变换,都是对向量X按照比例压缩再进行平移。
标准化和中心化的区别:标准化是原始分数减去平均数然后除以标准差,中心化是原始分数减去平均数。 所以一般流程为先中心化再标准化。 为什么要归一化/标准化? 归一化/标准化实质是一种线性变换,线性变换有很多良好的性质,这些性质决定了对数据改变后不会造成“失效”,反而能提高数据的表现,这些性质是归一化/标准化的前提。比如有一个很重要的性质:线性变换不会改变原始数据的数值排序。
Batch归一化会使参数搜索问题变得很容易,使神经网络对超参数的选择更加稳定,超参数的范围会更加庞大,工作效果也很好,也会使训练更加容易.
nomarlizaing:
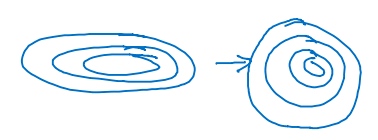
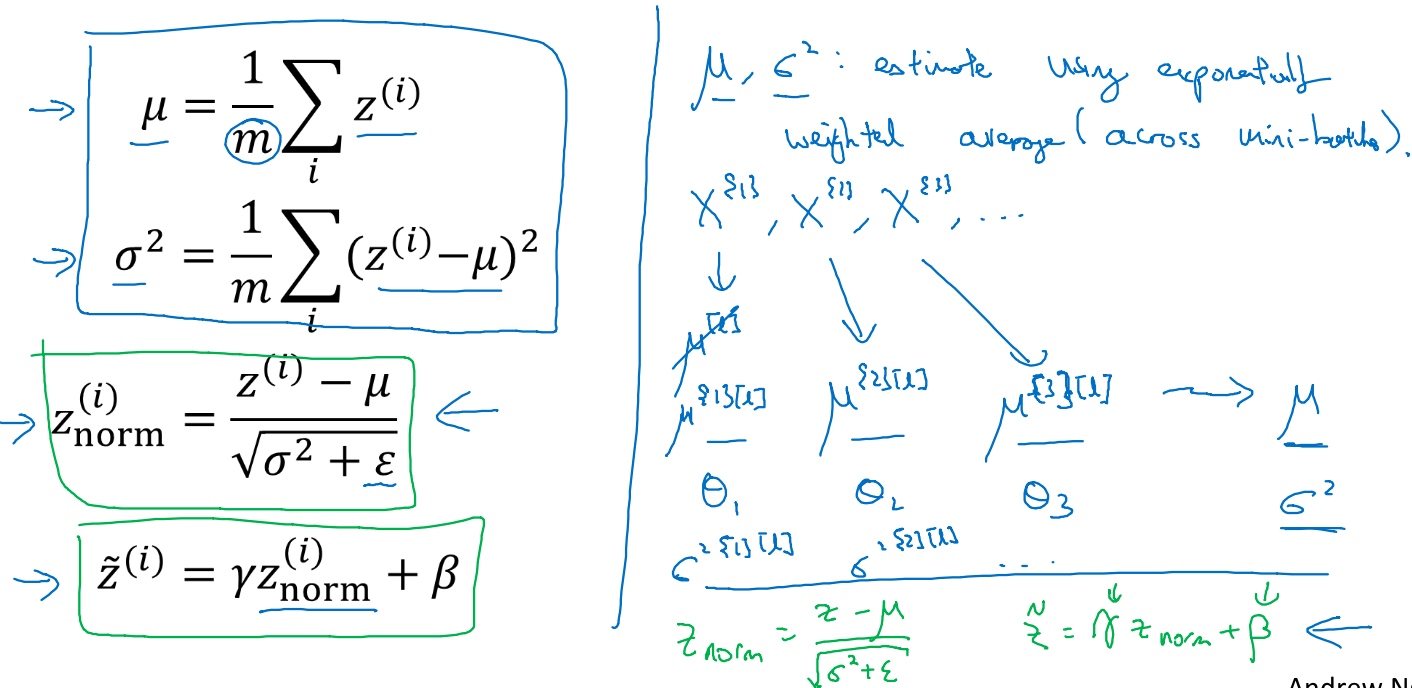
归一化输入特征可以加快学习过程: 计算了平均值,从训练集中减去平均值,计算了方差,接着根据方差归一化数据集; 轮廓由长变圆, 更易于算法优化.
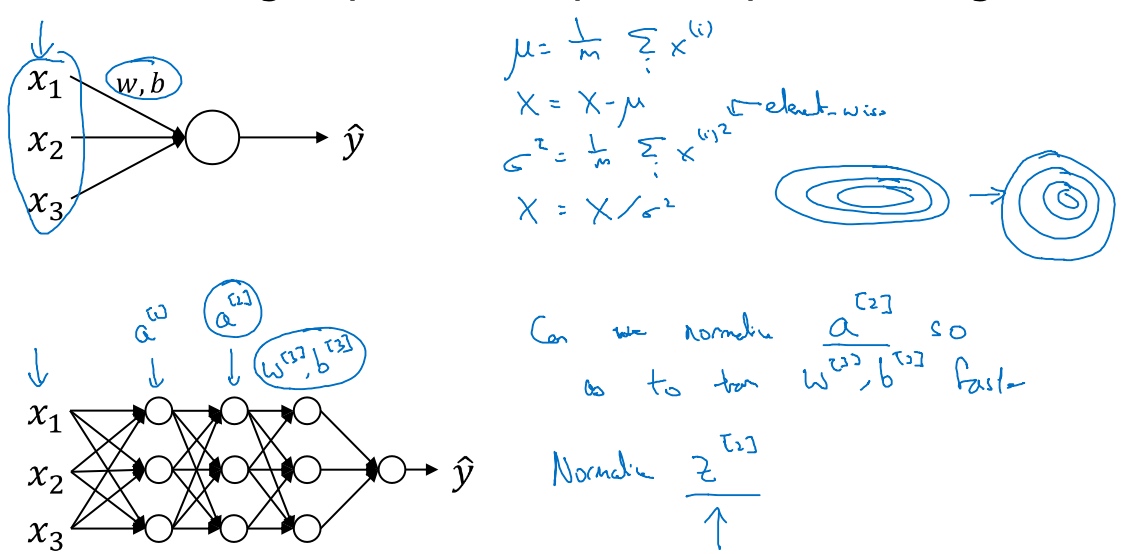
通过归一化$a^{[2]}$的值, 来更快的训练$W^{[3]},b^{[3]}$. (因为$a^{[2]}$是下一层的输入, 所以就会影响$W^{[3]},b^{[3]}$的训练)
通常都是normalizaing 线性函数Z 而不是 激活函数A.

Give some intermediate values in NN $Z^{(i)},...,Z^{(m)}$
方法如下, 减去均值再除以标准偏差, 为了使数值稳定, 通常将$epsilon$作为分母,以防$\alpha=0$的情况
$$
\mu = \frac{1}{m}\sum_i Z^{(i)} \\
\sigma^2 = \frac{1}{m}\sum_i (Z^{(i)} - \mu)^2 \\
Z^{(i)}_{norm} = \frac{Z^{(i)} - \mu}{\sqrt{\sigma^2 + \epsilon}}
$$
$Z^{(i)}_{norm}$已经标准化, 化为含平均值0和标准单位方差(方差1). 但不想让隐藏单元总是含有平均值0和方差1. 所以:
$$
\tilde{Z}^{(i)} = \gamma Z^{(i)}_{norm} + \beta
$$
where $\gamma,\beta$ are learnable parameter, 所以可以使用梯度下降算法来更新它们; 它们的作用是让你可以随机设置$\tilde{Z}$的平均值.
如果
$\gamma = \sqrt{\sigma^2 + \epsilon}$
$\beta = \mu$
那么 $\tilde{Z}^{(i)} = Z^{(i)}$.
通过赋予$\gamma,\beta$其它值,可以构造含其它平均值和方差的隐藏单元值.
将 Batch Norm 拟合进神经网络(Fitting Batch Norm into a neural network)

把输入X拟合到第一隐藏层, 然后计算$z^{[1]}$, 这是由$w^{[1]},b^{[1]}$两个参数控制的. 接着, 把$z^{[1]}$值进行Batch归一化(BN), 由$\beta^{[1]},\gamma^{[1]}$两参数控制, 得到$\tilde{z}^{[1]}$, 然后将其输入激活函数$a^{[1]}$, 即$a^{[1]}= g^{[1]}(\tilde{z}^{[1]})$, 其他隐藏层同理.
所以网络的参数就会是$w^{[1]},b^{[1]},\beta^{[1]},\gamma^{[1]}$
(注意: 这里的$\beta$和Adam算法里的$\beta$完全不同/没有关系)
在TensorFlow框架中, 可以用这个函数tf.nn.batch_normalization实现
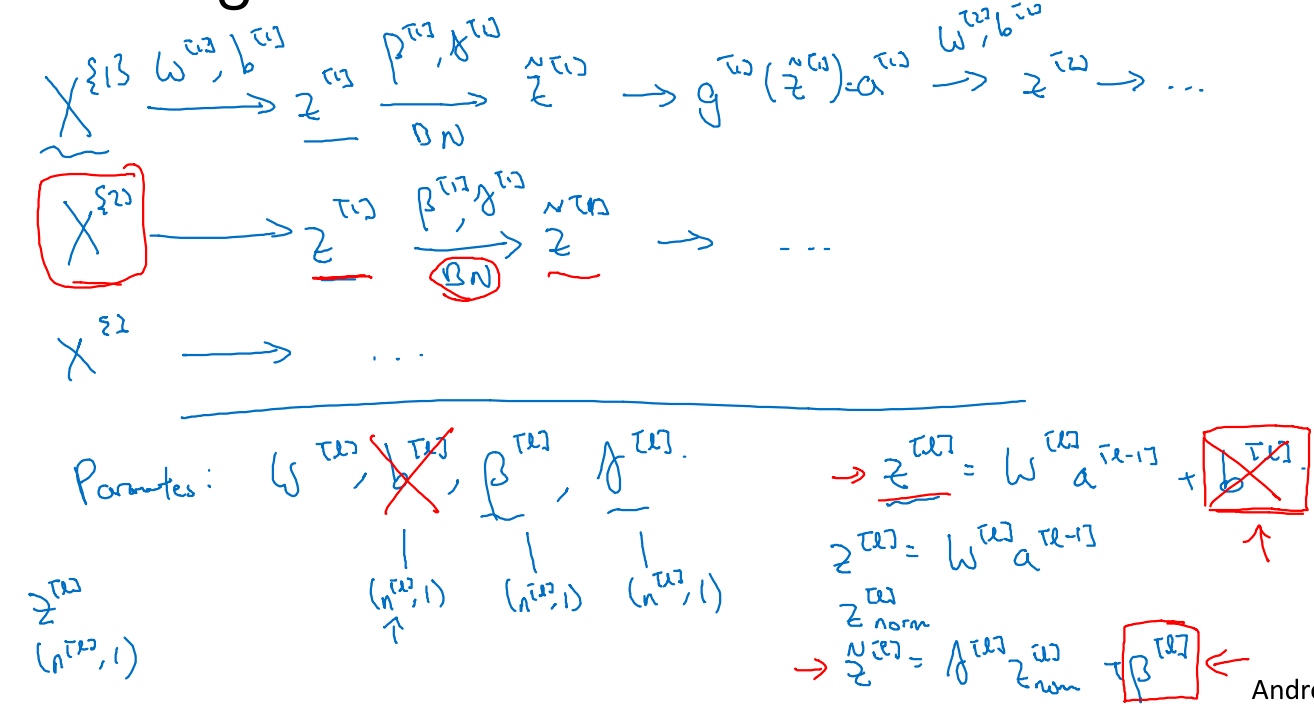
实践中, Batch归一化通常和训练集的mini-batch一起使用, 如图.
注意!
计算z的方式 $z^{[l]}=w^{[l]}a^{[l-1]}+b^{[l]}$, 但Batch归一化做的是先将$z^{[l]}$归一化,结果为均值0和标准方差,再由$\gamma, \beta$缩放, 这意味着$b^{[l]}$的值无论是多少, 都要被减去, 因为

总结:
使用mini-batch梯度下降法, 运行t=1到batch数量的for循环
1. 在mini-batch 上对每个隐藏层应用正向prop, 用Batch归一化, $\tilde{z}^{[l]}$代替$z^{[l]}$. (它确保在这个mini-batch中,z值有归一化的均值和方差)
2. 用反向prop计算$dw^{[l]},db^{[l]},d\beta^{[l]},d\gamma^{[l]}$ (严格来说, 没有$db^{[l]}$, b已经去掉了)
3. 更新这些参数 $w^{[l]} := w^{[l]} - \alpha dw^{[l]}$ 其他同理
可以使用Momentum、RMSprop、Adam的梯度下降法更新mini-batch优化参数.
Batch Norm 为什么奏效?(Why does Batch Norm work?)
为什么Batch归一化会起作用呢?
原因1. 通过归一化所有的输入特征值x,以获得类似范围的值,可以加速学习
原因2. 可以使权重比你的网络更滞后或更深层,比如,第10层的权重更能经受得住变化,相比于神经网络中前层的权重
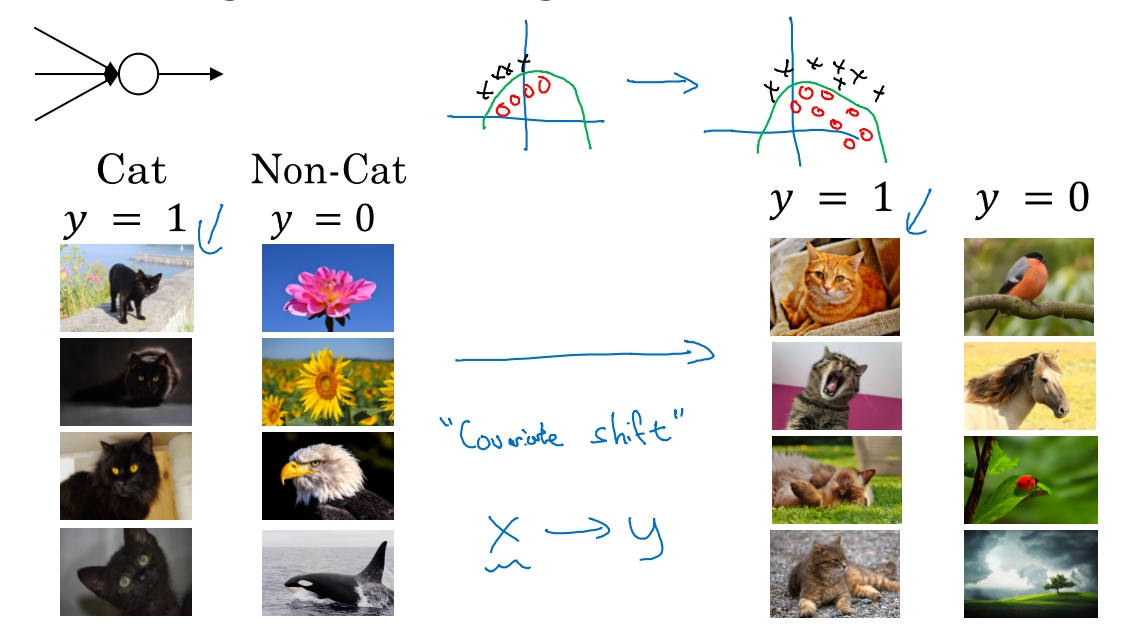
一个神经网络, 用于猫脸识别检测, 假设已经在所有黑猫的图像上训练了数据集(左边), 现在要把此网络应用于有色猫(右边), cosface(新的人脸识别的损失函数)可能适用的不会很好. Covariate shift问题 - 数据改变分布. 如果已经学习了x到y的映射,如果x的分布改变了,那么可能需要重新训练你的学习算法.
Why this is a problem with neural networks?

Batch归一化做的,是它减少了隐藏值分布变化的数量(减少了输入值改变的问题,使这些值变得更稳定,神经网络的之后层就会有更坚实的基础). 它做的是当前层保持学习,当改变时,迫使后层适应的程度减小了,你可以这样想,它减弱了前层参数的作用与后层参数的作用之间的联系,它使得网络每层都可以自己学习,稍稍独立于其它层,这有助于加速整个网络的学习
Batch归一化还有一个作用,它有轻微的正则化效果. 和dropout相似,它往每个隐藏层的激活值上增加了噪音,dropout有增加噪音的方式,它使一个隐藏的单元,以一定的概率乘以0,以一定的概率乘以1,所以你的dropout含几重噪音,因为它乘以0或1。对比而言,Batch归一化含几重噪音,因为标准偏差的缩放和减去均值带来的额外噪音。这里的均值和标准差的估计值也是有噪音的,所以类似于dropout,Batch归一化有轻微的正则化效果,因为给隐藏单元添加了噪音,这迫使后部单元不过分依赖任何一个隐藏单元. 通过应用较大的min-batch,你减少了噪音,因此减少了正则化效果,这是dropout的一个奇怪的性质,就是应用较大的mini-batch可以减少正则化效果
- Batch Norm as regularization Each mini-batch is scaled by the many/variance computed on just that mini-batc
- This adds some noise to the values z1 within that minibatch. So similar to dropout, it adds some noise to each hidden layer’s activations
- This has a slight regularization effect
测试时的 Batch Norm(Batch Norm at test time)
Batch归一化将数据以mini-batch的形式逐一处理,但在测试时,可能需要对每个样本逐一处理.


Softmax 回归(Softmax regression)
Softmax 回归, 用来多分类.

猫做类1,狗为类2,小鸡是类3, 其他是类0
用大写的C来表示输入会被分入的类别总个数.
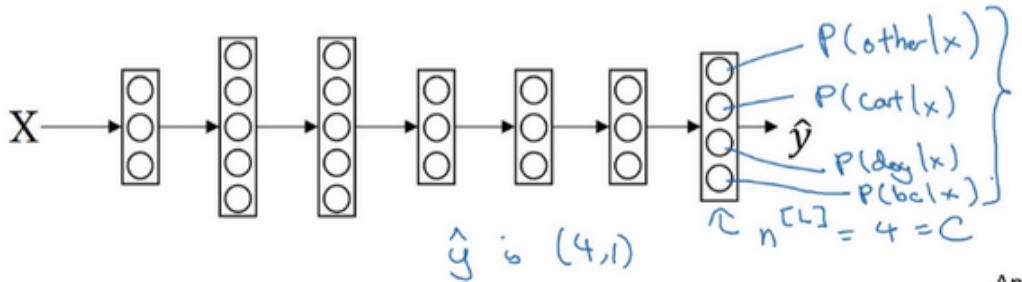
这个神经网络的输出层有4个输出单元(C个输出单元), 代表每个类型的概率有多大. 所以$\tilde{y}$是一个4 x 1的向量,4个加起来应为1.
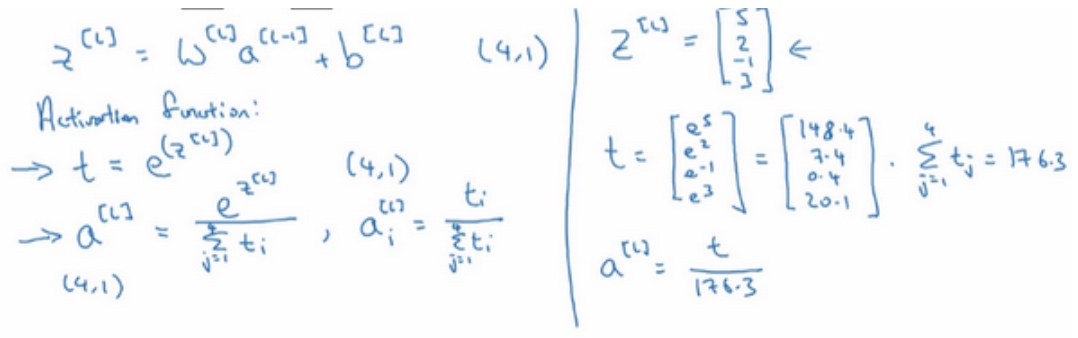
$z^{[l]}=W^{[l]}a^{[l-1]}+b^{[l]}$后用Softmax激活函数:
1. 印个临时变量t, $t = e^{z^{[l]}}$
2. $a^{[l]} = \frac{e^{z^{[l]}}}{\sum^{4}_{j=1}t_i}$
例子:
$z^{[l]} = \begin{bmatrix} 5 \\ 2 \\ -1\\ 3 \end{bmatrix}\quad$ 所以$t^{[l]} = \begin{bmatrix} e^5 \\ e^2 \\ e^{-1}\\ e^3 \end{bmatrix}\quad = \begin{bmatrix} 148.4 \\ 7.4 \\ 0.4\\ 20.1 \end{bmatrix}\quad$, 相加的176.3
所以$a^{[l]} = \frac{t}{176.3}$.
如第一个节点, 它会输出$\frac{e^5}{176.3} = 0.842$, 表示是类0的概率就是84.2%;
最后总的得到$a^{[l]} = \tilde{y} =\begin{bmatrix} 0.842 \\ 0.042 \\ 0.002\\ 0.114 \end{bmatrix}\quad$, 总和为1.
之前的激活函数Sigmoid和ReLu都是接受单行数值输入, 输出一个实数. Softmax激活函数的特殊之处在于,因为需要将所有可能的输出归一化,就需要输入一个向量,最后输出一个向量.
Softmax Example:
训练一个 Softmax 分类器(Training a Softmax classifier)
根据之前的例子, Softmax激活函数的输出:
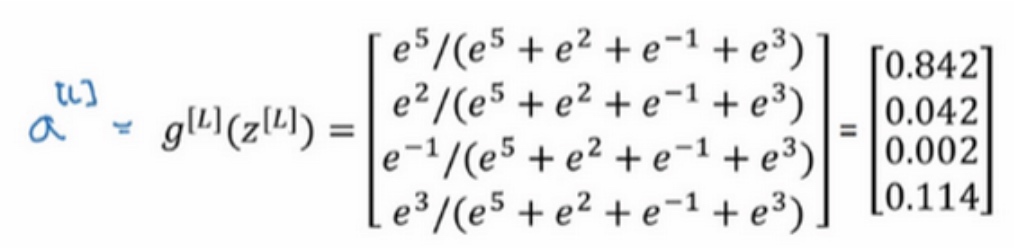
Softmax这个名称的来源是与所谓hardmax对比,hardmax会把向量z变成这个向量$\begin{bmatrix} 1 \\ 0 \\ 0 \\ 0 \end{bmatrix}\quad$, 在z中最大元素的位置上放1, 其他位置放0. 而softmax所做是从z到概率的映射, 更为温和.
对于Softmax回归, 如果C=2, 实际上它就变成了logistic回归.
softmax的损失函数(Loss function): $L(\tilde{y},y) = -\sum^m_{j=1}y_jlog\tilde{y}_j$
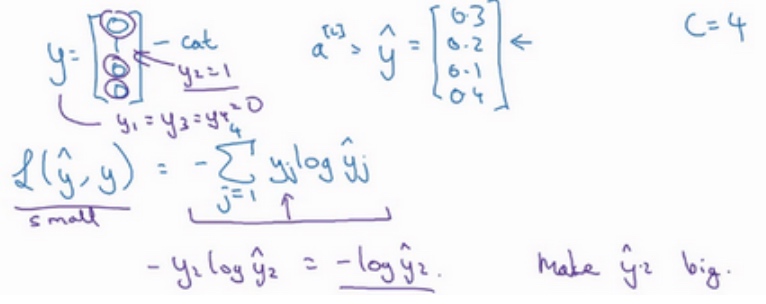
样本中$y_1 = y_3=y_4 = 0$, 只用$y_2=1$, 所以$L(\tilde{y},y) = -y_2log\tilde{y}_2 = -log\tilde{y}_2$
所以如果学习算法(梯度下降…)试图将它变小(训练集的损失), 要使它变小的唯一方式就是使$-log\tilde{y}_2$
变小, 要想做到这一点, 就需要使$\tilde{y}_2$尽可能大. 所以$\tilde{y}$向量里面的某个值越大, 则获得的损失函数值越小.
概括来讲,损失函数所做的就是它找到你的训练集中的真实类别,然后试图使该类别相应的概率尽可能地高,这其实就是最大似然估计的一种形式
前面是单个样本的损失, 而整个训练集的损失:
$J(w^{[1]},w^{[2]},...,w^{[m]}) = \frac{1}{m}\sum^m_{i=1}L(\tilde{y},y)$

Softmax的梯度下降

$dz^{[l]} = \tilde{y} - y$
深度学习框架(Deep Learning frameworks)
深度学习框架,能让实现神经网络变得更简单
- Caffe/Caffe2
- CNTK
- DL4J
- Keras
- Lasagne
- mxnet
- PaddlePaddle
- TensorFlow
- Theano
- Torch
Criteria of Choosing deep learning frameworks:
- Ease of programming (development and deployment)
- Running speed
- Truly open (open source with good governance)
TensorFlow
Code example:
import numpy as np
import tensorflow as tf
coefficients = np.array([[1], [-20], [25]])
w = tf.Variable([0],dtype=tf.float32)
x = tf.placeholder(tf.float32, [3,1])
cost = x[0][0]*w**2 + x[1][0]*w + x[2][0] # (w-5)**2
train = tf.train.GradientDescentOptimizer(0.01).minimize(cost)
init = tf.global_variables_initializer()
# session = tf.Session()
# session.run(init)
# print(session.run(w))
with tf.Session() as session:
session.run(init)
print(session.run(w))
for i in range(1000):
session.run(train, feed_dict={x:coefficients})
print(session.run(w))TensorFlow程序的核心是计算损失函数,然后TensorFlow自动计算出导数,以及如何最小化损失,因此这行代码cost =x[0][0]*w**2 +x[1][0]*w + x[2][0]#(w-5)**2所做的就是让TensorFlow建立计算图

TensorFlow的优点在于,通过用这个计算损失,计算图基本实现前向传播,TensorFlow已经内置了所有必要的反向函数, 它能自动用反向函数来实现反向传播, 这是编程框架能帮你变得高效的原因之一.
- l [return]