训练，验证，测试集（Train / Dev / Test sets）

数据集, 三部分

• 训练集(training set)
• 验证集(dev set / holdout cross validation set)
• 测试集(test set)

In previous era: Data set(100, 1000, 10000)

• 70 / 30% or
• 60 / 20 / 20 %

Big data era: Data set(1M or above)

• 98 / 1/ 1 %
• 99.5 / 0.4 / 0/1 %

其他:

• 验证集和测试集偏向来自同一个分布.
• 测试集的目的是对最终所选定的神经网络系统做出无偏估计, 如果不需要无偏估计, 也可以不设置测试集
• 只有验证集，没有测试集，要做的就是，在训练集上训练，尝试不同的模型框架，在验证集上评估这些模型，然后迭代并选出适用的模型
• 有时候, 验证集会被称为测试集

偏差, 方差（Bias /Variance）

bias-variance trade-off

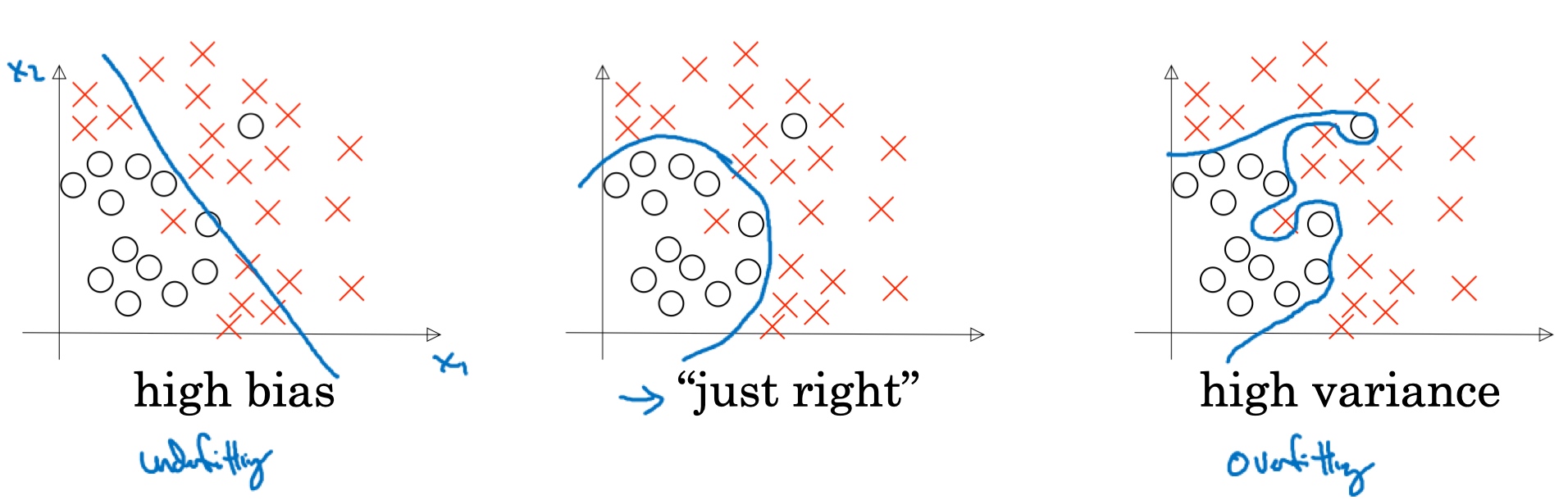
如果给最左数据集拟合一条直线，可能得到一个逻辑回归拟合，但它并不能很好地拟合该数据，这是高偏差（high bias）的情况，称为“欠拟合”（underfitting).

相反的, 如果拟合一个非常复杂的分类器，比如深度神经网络或含有隐藏单元的神经网络，可能就非常适用于这个数据集(最右)，但是这看起来也不是一种很好的拟合方式分类器方差较高（high variance), 数据过度拟合（overfitting).

在两者之间，可能还有一些像中间这样的，复杂程度适中，数据拟合适度的分类器，这个数据拟合看起来更加合理，称之为“适度拟合”（just right）是介于过度拟合和欠拟合中间的一类.

通过误差去判断属于高方差还是高偏差:

1. 在训练集的错误率仅1%, 而在验证集的错误率有11%, 说明模型太过拟合训练集, 可以从两者看出这是高方差.
2. 在训练集的错误率15%, 而在验证集的错误率有16%, 数据在训练集的拟合度不高, 两者的错误率都偏高, 可以看出这是高偏差的.
3. 在训练集的错误率15%, 而在验证集的错误率有39%, 高方差和高偏差. 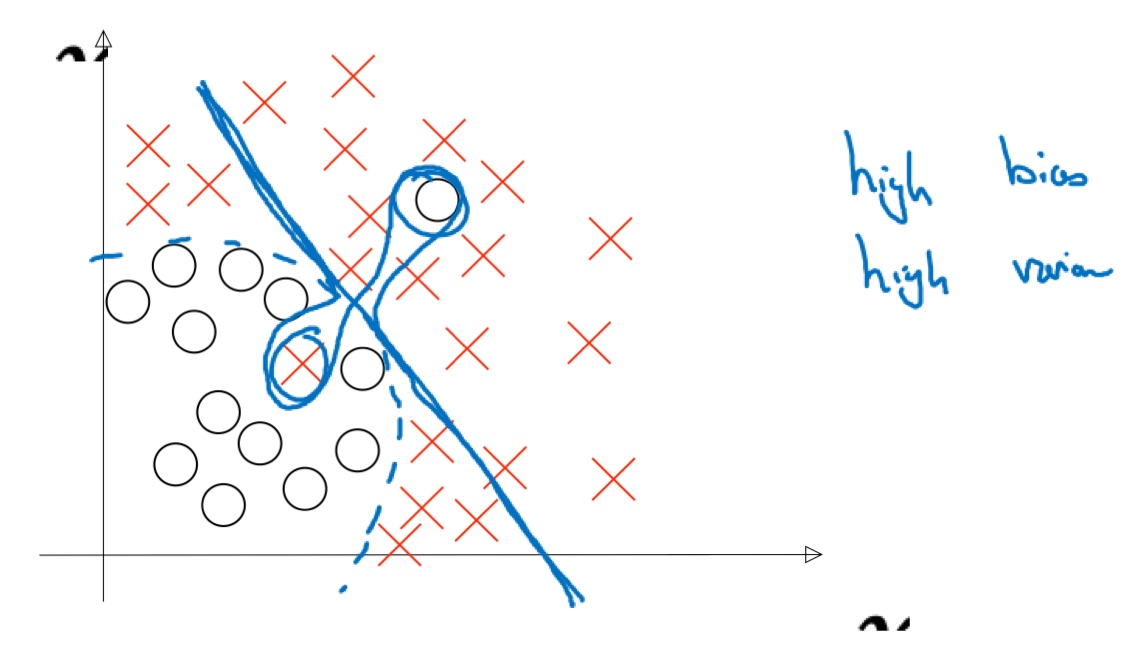(有些区域高偏差, 有些区域高方差)
4. 在训练集的错误率05%, 而在验证集的错误率有1%, 低方差和低偏差.

以上结论是在optimal(Bayes) error = 0%的前提下.

若最优(贝叶斯)误差为15% (可能照片像素差, 人和系统都难以辨别), 则情况2是正常的

机器学习基础（Basic Recipe for Machine Learning）

训练神经网络用到的基本方法:

若偏差高(取决于训练集的performance):

1. 选择一个新的规模更大的网络(含有更多隐藏层, 隐藏单元)
2. 花费更多时间来训练网络
3. 尝试不同的神经网络架构

若方差高(取决于验证集的performance):

1. 采用更多数据
2. 通过正则化减少拟合
3. 尝试不同的神经网络架构

注意:

1. 先判断是高偏差还是方差, 再采取不同策略
2. 偏差方差权衡(bias-variance trade-off)

只要正则适度，通常构建一个更大的网络便可以在不影响方差的同时减少偏差，而采用更多数据通常可以在不过多影响偏差的同时减少方差。这两步实际要做的工作是：训练网络，选择网络或者准备更多数据，现在我们有工具可以做到在减少偏差或方差的同时，不对另一方产生过多不良影响.

正则化（Regularization）

正则化通常有助于避免过拟合或减少网络误差.

加正则化项, 避免数据权值矩阵W过大.

逻辑回归的正则化项:

正则化项:

$\frac{\lambda}{2m}||w||^2_2$

(分母是m还会2m, 都只是一个比例常量而已)

L2 regularlization: $||w||^2_2 = \sum^{n_x}_{j=1}w^2_j = w^Tw$

(使用L1正则化, w最终会是稀疏的)

参数b的正则化通常不写, 因为w是一个高维度参数矢量, 已经可以表达高偏差问题. w几乎涵盖所有参数, b加不加没多大影响.

神经网络的正则化项:

正则项为: $\frac{\lambda}{2m}\sum_{l=1}^L||w^{[l]}||^2_F$

该矩阵范数被称作“弗罗贝尼乌斯范数”，用下标F标注.

具体来看:

$||w^{[l]}||^2_F = \sum_{i=1}^{n^{[l]}}\sum_{j=1}^{n^{[l-1]}} (w^{[l]}_{ij})^2$

${n^{[l]}}, {n^{[l-1]}}$分别表示l和l-1层的隐藏单元数量

梯度下降:

原公式: $W^{[l]} := W^{[l]} - \alpha dW^{[l]}$

加入正则化项后的$dW^{[l]}$:$ (form\;backprop) +\frac{\lambda}{m}W^{[l]}$

新公式: $$ W^{[l]} := W^{[l]} - \alpha [(form\;backprop) +\frac{\lambda}{m}W^{[l]}] \\ = W^{[l]} - \alpha \frac{\lambda}{m}W^{[l]} - \alpha (form\;backprop) \\ = (1-\alpha \frac{\lambda}{m})W^{[l]} - \alpha (form\;backprop) $$

注: $(1-\alpha \frac{\lambda}{m})$这个系数<1

该正则项说明，不论$W^{[l]}$是什么，都试图让它变得更小，实际上，相当于给矩阵W乘以$(1-\alpha \frac{\lambda}{m})$倍的权重，矩阵W减去$\alpha \frac{\lambda}{m}$倍的它，也就是用这个系数$(1-\alpha \frac{\lambda}{m})$乘以矩阵W，该系数小于1，因此L2范数正则化也被称为“权重衰减”.

为什么正则化有利于预防过拟合

例子1:

Why shrinking the L2 norm (the parameters) might cause less overfitting?

Intuition: If you crank up regularization lambda to be really big, weight matrices W to be reasonably close to 0, thats zeroing out the impact of hidden units. It simplified neural network, but stacked most probably as deep .

A smaller neural network that is less prone to overfitting.

如果正则化$\lambda$设置得足够大, W权重矩阵被设置为接近于0的值, 就等于把多隐藏单元的权重设为0, 于是就消除了这些隐藏单元的许多影响, 神经网络会变成一个很小的网络, 可是深度却很大, 使这个网络从过度拟合的状态更接近左图的高偏差状态.

例子2:

使用双曲线激活函数, 只要z非常小，如果z只涉及少量参数，就只利用了双曲正切函数的线性状态 (图中圈起来的红色线性部分) 只要z值更大或者更小, 激活函数开始变得非线性.

如果正则化参数λ很大, 参数W权重矩阵就会很小, 所以激活函数的参数z也会相对较小. z的取值范围小, 曲线函数会相对呈线性, 整个神经网络会计算离线性函数近的值, 这个线性函数非常简单, 并不是一个极复杂的高度非线性函数, 所以不会发生过拟合.

code:

W1 = parameters["W1"]
W2 = parameters["W2"]
W3 = parameters["W3"]
    
cross_entropy_cost = compute_cost(A3, Y) # This gives you the cross-entropy part of the cost
    
L2_regularization_cost = (lambd / 2) *(np.sum(np.square(W1))+np.sum(np.square(W2))+np.sum(np.square(W3))) / m

    
cost = cross_entropy_cost + L2_regularization_cost

dZ3 = A3 - Y
    
dW3 = 1. / m * np.dot(dZ3, A2.T) + (lambd * W3) / m
db3 = 1./m * np.sum(dZ3, axis=1, keepdims = True)
...

dropout 正则化（Dropout Regularization）

另外一个实用的正则化方法: Dropout (随机失活)

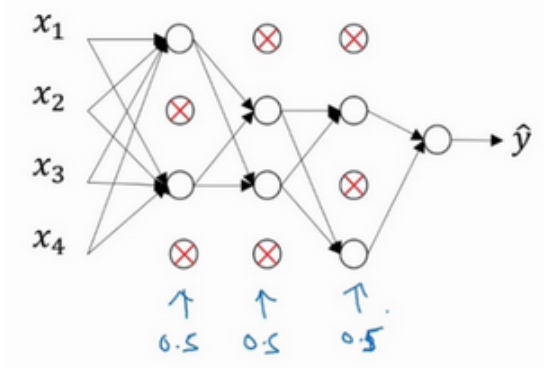
假设网络中的每一层，每个节点都以抛硬币的方式设置概率，每个节点得以保留和消除的概率都是0.5. 设置完节点概率, 会消除一些节点和删除掉从该节点进出的连线, 最后得到一个节点更少, 规模更小的网络, 然后用backprop方法进行训练.

反向随机失活（inverted dropout）

是最常用的dropout方法

用一个三层（l=3）网络来举例说,

$d^{[3]}$表示一个三层的dropout向量:

d3 = np.random.rand(a3.shape[0],a3.shape[1]) < keep-prob

keep-prop表示保留某个隐藏单元的概率, 这里用0.8. 所以$d^{[3]}$中有八成的数字是1(True), 二成是0(False).

然后,

a3 =np.multiply(a3,d3) 元素相乘. 作用是让$d^{[3]}$中0元素与$a^{[3]}$中相对元素归零. (注, 元素等于0的概率只有20%)

最后, $a^{[3]}$除以keep-prob参数,0.8. 这么做的原因:

• 假设第三隐藏层上有50个隐藏单元
• 保留和删除它们的概率分别为80%和20%, 这意味着最后被删除或归零的单元平均有10个（50×20%=10)

• 考虑$z^{[4]} = w^{[4]}a^{[3]}+b^{[3]}$, $a^{[3]}$中有20%的元素被归零, 为了不影响$z^{[4]}$的期望值, 需要用$w^{[4]}a^{[3]}/0.8$, 它将会修正或你不所需的20%, $a^{[3]}$的期望值不会变

  (反向随机失活（inverted dropout）方法通过除以keep-prob，确保$a^{[3]}$的期望值不变)

在测试阶段不使用dropout, 因为不期望输出结果是随机的, 如果测试阶段应用dropout函数, 预测会受到干扰.

理解 dropout（Understanding Dropout）

直观上理解：不要依赖于任何一个特征, 因为特征(该单元的输入)可能被随机清除(dropout). 如果一个单元通过这种方式传播下去, 并为这个单元的输入增加一点权重(权重不会太大, 因为特征会被随机清除, 所以它不会依赖任意一个特征), 通过传播所有权重, dropout将产生收缩权重的平方范数的效果, 和之前讲的L2正则化类似;

实施dropout的结果实际上它会压缩权重, 最终达到防止过拟合的效果;

然而, L2对不同权重的衰减是不同的, 它取决于激活函数倍增的大小.

总结一下, dropout的功能类似于L2正则化, 与L2正则化不同的是应用方式不同会带来一点点小变化, 甚至更适用于不同的输入范围.

在神经网络不同层上的keep-prob是可以变化的. 上图, 第一层，矩阵$W^{[1]}$是7×3，第二个权重矩阵$W^{[2]}$是7×7，第三个权重矩阵$W^{[1]}$是3×7. $W^{[2]}$是最大的权重矩阵, 拥有最大的参数集, 因此它的keep-prob值应该相对较低. 假设这里keep-prop是0.5, 其他层可能是0.⁸⁄₀.⁹⁄₁.0, 而输入层通常都是1.0.

小结, 如果担心某些层比其它层更容易发生过拟合(含有诸多参数的层), 可以把keep-prob设置成比较小的值, 以便应用更强大的dropout; 反之亦然.

dropout在计算视觉中使用频繁:

计算视觉中的输入量非常大, 输入太多像素, 以至于没有足够的数据, 所以存在过拟合. 但是, 注意dropout是一种正则化方法, 它有助于预防过拟合，因此除非算法过拟合, 不然我不要使用dropout.

dropout缺点:

代价函数不再被明确定义, 每次迭代, 都会随机移除一些节点, 这是很难进行复查的. 所以, 通常将keep-prob的值设为1, 运行代码, 确保J函数单调递减, 通过调试工具来绘制图像. 最后才打开dropout函数.

Code:

forward prop

# LINEAR -> RELU -> LINEAR -> RELU -> LINEAR -> SIGMOID
Z1 = np.dot(W1, X) + b1
A1 = relu(Z1)
 # Step 1: initialize matrix D1 = np.random.rand(..., ...)
D1 = np.random.rand(A1.shape[0], A1.shape[1])
# Step 2: convert entries of D1 to 0 or 1 (using keep_prob as the threshold)
D1 = (D1 < keep_prob)
# Step 3: shut down some neurons of A1
A1 = A1*D1
# Step 4: scale the value of neurons that haven't been shut down
A1 /= keep_prob

back prop

dZ3 = A3 - Y
dW3 = 1./m * np.dot(dZ3, A2.T)
db3 = 1./m * np.sum(dZ3, axis=1, keepdims = True)
dA2 = np.dot(W3.T, dZ3)
# Step 1: Apply mask D2 to shut down the same neurons as during the forward propagation
dA2 *= D2
# Step 2: Scale the value of neurons that haven't been shut down
dA2 /= keep_prob

dZ2 = np.multiply(dA2, np.int64(A2 > 0))
dW2 = 1./m * np.dot(dZ2, A1.T)
db2 = 1./m * np.sum(dZ2, axis=1, keepdims = True)
...

其他正则化方法（Other regularization methods）

一, 数据扩增(Data Augumentation)

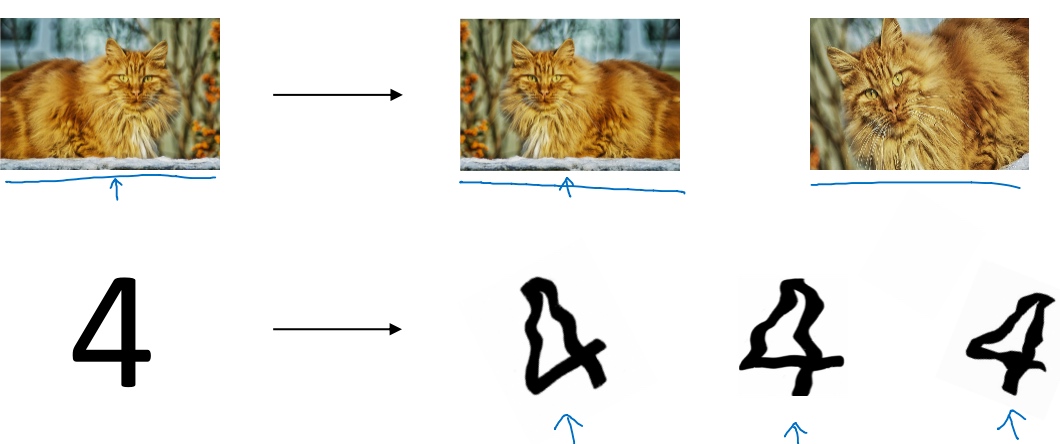
通过图片反转, 旋转, 剪裁..产生额外的假训练数据, 从而增大数据集.

二, 提早停止训练神经网络(Early stopping)

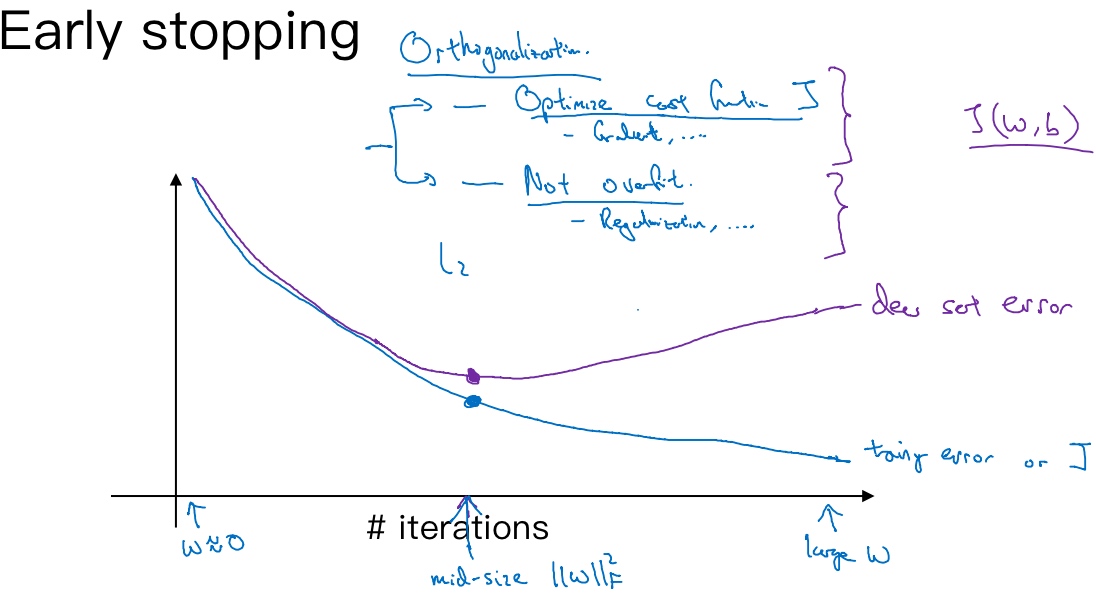
运行梯度下降时, 除了可以绘制训练误差, 或只绘制代价函数J的优化过程, 还可以绘制验证集误差. 验证集误差通常会先呈下降趋势, 然后在某个节点处开始上升.

而early stopping的作用就是在中间点停止迭代过程, 得到一个w值中等大小的弗罗贝尼乌斯范数.

机器学习的过程

• Optimize cost function J
  • Gradient descent, momentum, Adam, RMSprop, …
• Prevent overfitting
  • regularization, …
• ….

正交化(Orthogonalization) - 在一个时间做一个任务

优点:

• 只运行一次梯度下降, 可以找出的较小值, 中间值和较大值, 而无需尝试正则化超参数$\lambda$的很多值

缺点:

• 不能独立地处理优化代价函数和防止过拟合. 提早停止虽然防止了过拟合, 但是因为提早停止梯度下降, 也就是停止了优化代价函数J, 导致代价函数J的值可能不够小

归一化输入（Normalizing inputs）

假设一个训练集有两个特征，输入特征为2维，归一化需要两个步骤：

1. 零均值
2. 归一化方差；

(无论是训练集和测试集都是通过相同的$\mu,\sigma^2$定义的数据转换)

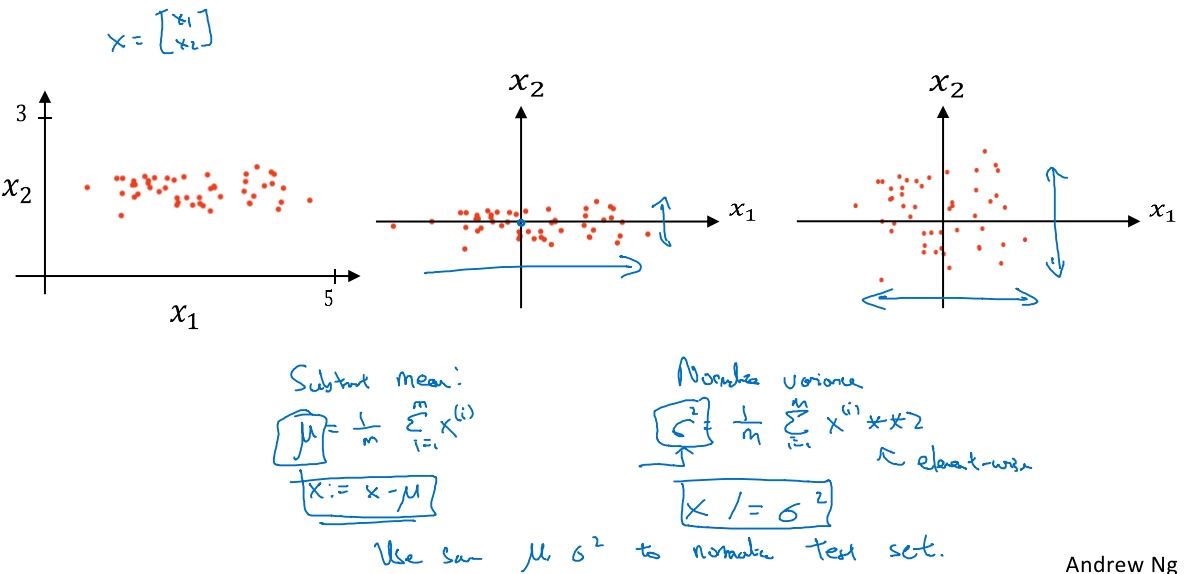
1. 零均值化, $\mu = \frac{1}{m}\sum^m_{i=1}x^{(i)}$, 它是一个向量, x等于每个训练数据x减去$\mu$, 得到中间的图.
2. 归一化方差, 特征x1的方差比特征x2的方差大得多. $\sigma^2 = \frac{1}{m}\sum^m_{i=1}(x^{(i)})^2$, 把所有数据除以向量$\sigma^2$, 得到最右的图.

使用非归一化的输入特征，代价函数会像左边的图(一个非常细长狭窄的代价函数), 因为特征值在不同范围，假如x1取值范围从1到1000，特征x2的取值范围从0到1，结果是参数w1和w2值的范围或比率将会非常不同. 梯度下降法可能需要多次迭代过程，直到最后找到最小值.

如果归一化特征，代价函数平均起来看更对称, 不论从哪个位置开始，梯度下降法都能够更直接地找到最小值，你可以在梯度下降法中使用较大步长.

小结:

如果输入特征处于不同范围内，可能有些特征值从0到1，有些从1到1000，那么归一化特征值就非常重要了. 确保所有特征都在相似范围内，通常可以帮助学习算法运行得更快

梯度消失/梯度爆炸（Vanishing / Exploding gradients）

训练深度神经网络所面临的一个问题就是梯度消失或梯度爆炸，也就是你训练神经网络的时候，导数或坡度有时会变得非常大，或者非常小，甚至于以指数方式变小，这加大了训练的难度.

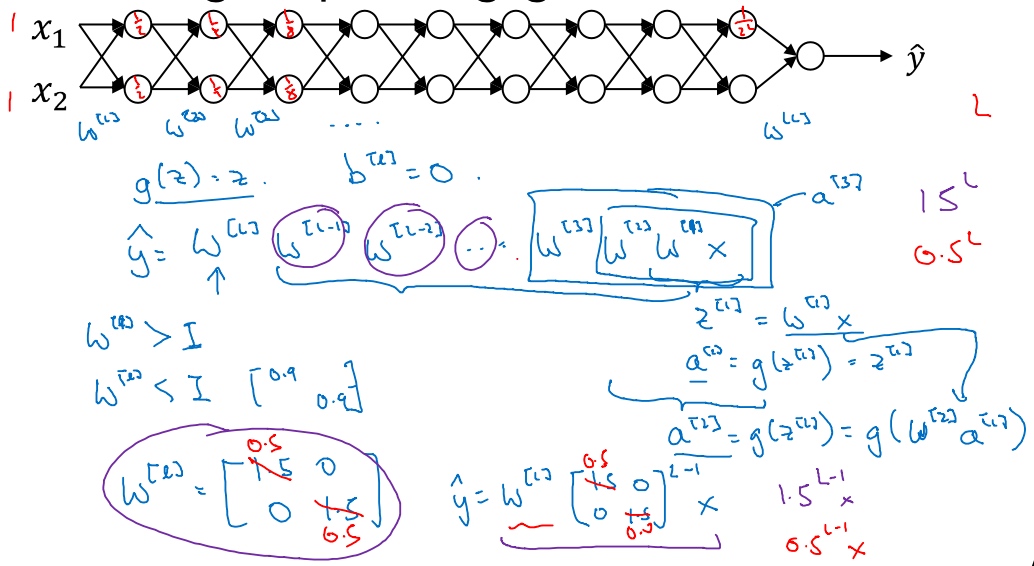
图中的的神经网络每层只有两个隐藏单元, 有参数$W^{[1]},W^{[2]},...,W^{[l]},$. 方便起见, 假设:

1. 使用线性激活函数g(z) = z
2. b = 0

则输出$y = W^{[l]}W^{[l-1]}...W^{[2]}W^{[1]}x$

因为 $$ Z^{[1]} = W^{[1]}x \\ a^{[1]} = g(Z^{[1]}) = Z^{[1]} \\ a^{[2]} = g(Z^{[1]}) = g(W^{[2]}a^{[1]}) = g(W^{[2]}W^{[1]}x) = W^{[2]}W^{[1]}x \\ ..... $$

权重W只比1 (单位矩阵) 略大一点, 深度神经网络的激活函数将爆炸式增长; 如果比1 (单位矩阵) 略小一点, 激活函数将以指数级递减.

明智地选择随机初始化权重，从而避免梯度消失或梯度爆炸.

神经网络的权重初始化（Weight Initialization for Deep NetworksVanishing / Exploding gradients）

单个神经元可能有4个输入特征，从x1到x4，经过a=g(z)处理，最终得到$\tilde{y}$.

$z = w_1x_1+w_2x_2+....+w_nx_n, b=0$, 暂时忽略b. 为了防止z值过大或过小, 所以希望n越大时, $w_i$越小, 因为z是$w_ix_i$的和. 所以最合理的方法就是设置$w_i = \frac{1}{n}$, n表示神经元的输入特征数量.

$w^{[l]} = np.random.randn(shape)*np.sqrt(\frac{1}{n^{[l-1]}})$, $n^{[l-1]}$就是喂给第$l$层神经单元的数量

(其中randn是来自零均值、方差为1的高斯分布取样)

如果使用Relu激活函数, 方差设为$\frac{2}{n}$效果会更好.

权重初始化：Why

在创建了神经网络后，通常需要对权重和偏置进行初始化，大部分的实现都是采取Gaussian distribution来生成随机初始值。假设现在输入层有1000个神经元，隐藏层有1个神经元，输入数据x为一个全为1的1000维向量，采取高斯分布来初始化权重矩阵w，偏置b取0。下面的代码计算隐藏层的输入z：

然而通过上述初始化后，因为w服从均值为0、方差为1的正太分布，x全为1，b全为0，输入层一共1000个神经元，所以z服从的是一个均值为0、方差为1000的正太分布。修改代码如下，生成20000万个z并查看其均值、方差以及分布图像：

输出结果如下：

输出图像如下：

在此情况下，z有可能是一个远小于-1或者远大于1的数，通过激活函数（比如sigmoid）后所得到的输出会非常接近0或者1，也就是隐藏层神经元处于饱和的状态。所以当出现这样的情况时，在权重中进行微小的调整仅仅会给隐藏层神经元的激活值带来极其微弱的改变。

而这种微弱的改变也会影响网络中剩下的神经元，然后会带来相应的代价函数的改变。结果就是，这些权重在我们进行梯度下降算法时会学习得非常缓慢。

因此，我们可以通过改变权重w的分布，使|z|尽量接近于0。这就是我们为什么需要进行权重初始化的原因了。

权重初始化：How

一种简单的做法是修改w的分布，使得z服从均值为0、方差为1的标准正态分布。根据正太分布期望与方差的特性，将w除以sqrt(1000)即可。修改后代码如下：

输出结果如下：

输出图像如下：

这样的话z的分布就是一个比较接近于0的数，使得神经元处于不太饱和的状态，让BP过程能够正常进行下去。

除了这种方式之外（除以前一层神经元的个数n_in的开方），还有许多针对不同激活函数的不同权重初始化方法，比如兼顾了BP过程的除以( (n_in + n_out)/2 )

梯度检验（Gradient checking）

有一个测试叫做梯度检验，它的作用是确保backprop正确实施.

对于一个函数来说，通常有两种计算梯度的方式：

• 数值梯度（numerical gradient）;
• 解析梯度（analytic gradient）;

数值梯度的优点是容易编程实现，不要求函数可微，然而，数值梯度缺点很明显，通常是近似解，同时求解速度很慢，因此在设计机器学习目标函数时，通常设计成可微的函数，可以快速地求解其解析梯度，同时这个梯度是确切解。

梯度检验就是通过估计梯度（导数）的近似值来估算我们的梯度下降算法算出(程序计算出来)的梯度（导数）是否为正确的.

(即通过数值梯度和解析梯度的对比来判断是否为正确)

上图中，我们关注$θ_0$点的函数的导数，即$θ_0$点切线（图中蓝线）的斜率，现在我们在$θ_0-ε$和$θ_0+ε$两点连一条线（图中红线），我们发现红线的斜率和蓝线斜率很相似.

红线的斜率可以用以下式子表示：

$\frac{J(θ_0+ε)-J(θ_0-ε)}{2ε}$ 实际上，以上的式子很好地表示了$θ_0$点导数的近似值。

在实际的应用中，θ往往是一个向量(所有参数的向量)，梯度下降算法要求我们对向量中的每一个分量进行偏导数的计算，对于偏导数，我们同样可以用以下式子进行近似计算：

$\frac{J(θ_1+ε,θ_2,θ_3...θ_n)-J(θ_1-ε,θ_2,θ_3...θ_n)}{2ε}$

上式很好地估计了损失函数对$θ_1$的偏导数.

梯度的数值逼近（Numerical approximation of gradients）

估计梯度（或导数）的近似值:

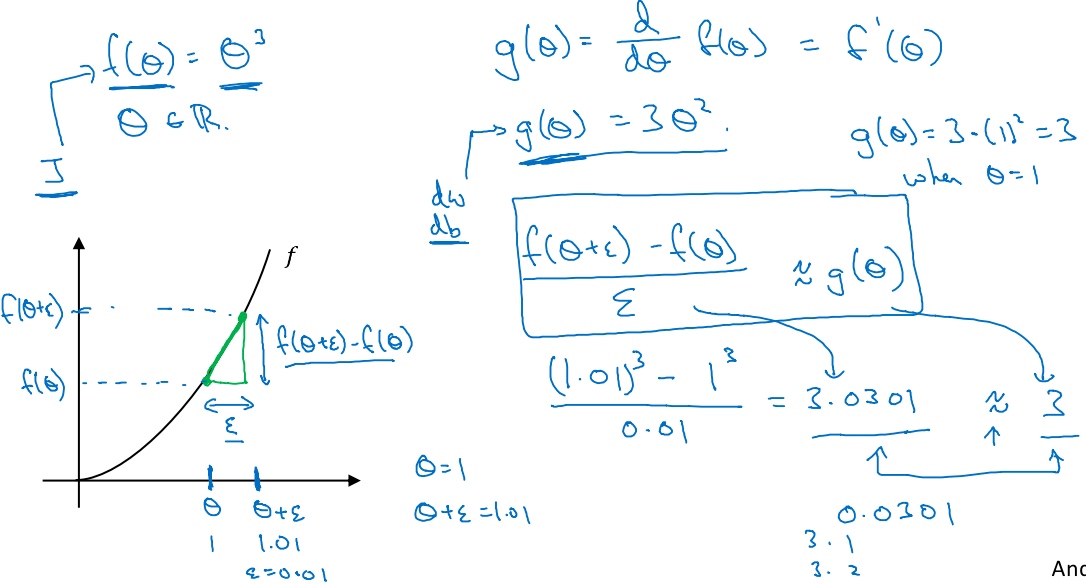
上面是单边检测误差的计算(误差0.03), 下面是双边检测误差的计算

双边检测误差更低(误差0.0001), 精度更高.

梯度检验（Gradient checking）

首先要把所有参数转化成一个巨大的向量数据$\theta$.

然后将J函数展开为$J(θ_1,θ_2,θ_3...)$,循环执行，从而对每个i也就是对每个$\theta$组成元素计算$d\theta_{approx}[i]$的值，使用双边误差:

$d\theta_{approx}[i] = \frac{J(θ_1,θ_2,..,θ_{i+ε},...)-J(θ_1-ε,θ_2,..,θ_{i-ε},...)}{2ε}$

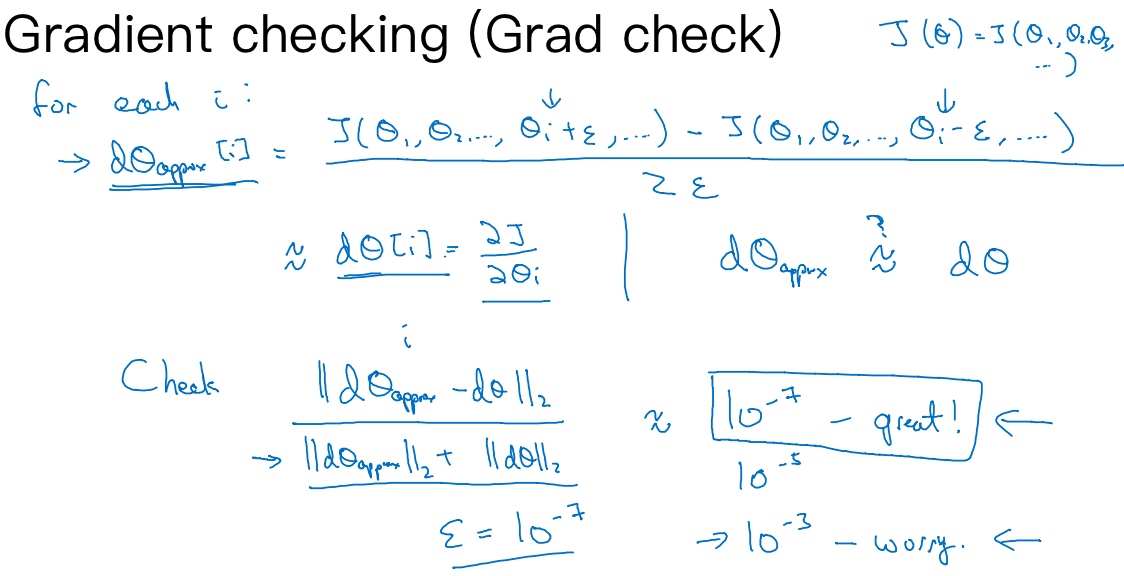
最后只需对比$d\theta_{approx}[i]$和$d\theta[i]$(代价函数的偏导数)

通常计算这两个向量的距离

$||d\theta_{approx} -d\theta||_2$

然后求平方根，得到欧式距离，然后用向量长度归一化，使用向量长度的欧几里得范数。分母只是用于预防这些向量太小或太大，分母使得这个方程式变成比率:

$$ \frac{||d\theta_{approx} -d\theta||_2}{||d\theta_{approx}||_2+||d\theta||_2} $$

通常采用 $\epsilon = 10^{-7}$ 作为检查解析梯度和数值梯度间差值的基准

梯度检验应用的注意事项（Gradient Checking Implementation Notes）

• Don’t use in training – only to debug
• If algorithm fails grad check, look at components to try to identify bug.
• Remember regularization.
• Doesn’t work with dropout.

• Run at random initialization; perhaps again after some training.

• 梯度检测方法的开销是非常大的，比反向传播算法的开销都大，所以一旦用梯度检测方法确认了梯度下降算法算出的梯度（或导数）值是正确的，那么就及时关闭它

• 一般来说ε的值选$10^{-4}$，注意并不是越小越好

• 双边形式的数值梯度在逼近解析梯度时效果比单边形式的数值梯度更好。

• 由于梯度检验的运行很慢，因此：

  • 进行梯度检验时，只使用一个或少数样本；
  • 在确认反向传播的实现代码无误后，训练神经网络时记得取消梯度检验函数的调用。

• 如果使用了 drop-out 策略，（直接进行）梯度检验会失效。可以在进行梯度检验时，将 keep-prob 设置为 1，训练神经网络时，再进行修改。

• 通常采用 e=10e-7 作为检查解析梯度和数值梯度间差值的基准。如果差值小于 10e-7，则反向传播的实现代码没有问题。

• 幸运的是，在诸如 TensorFlow、PyTorch 等深度学习框架中，我们几乎不需要自己实现反向传播，因为这些框架已经帮我们计算好梯度了；但是，在成为一个深度学习工作者之前，动手实现这些算法是很好的练习，可以帮助我们理解其中的原理。

code:

def gradient_check_n(parameters, gradients, X, Y, epsilon = 1e-7):
    """
    Checks if backward_propagation_n computes correctly the gradient of the cost output by forward_propagation_n
    
    Arguments:
    parameters -- python dictionary containing your parameters "W1", "b1", "W2", "b2", "W3", "b3":
    grad -- output of backward_propagation_n, contains gradients of the cost with respect to the parameters. 
    x -- input datapoint, of shape (input size, 1)
    y -- true "label"
    epsilon -- tiny shift to the input to compute approximated gradient with formula(1)
    
    Returns:
    difference -- difference (2) between the approximated gradient and the backward propagation gradient
    """
    
    # Set-up variables
    parameters_values, _ = dictionary_to_vector(parameters)
    grad = gradients_to_vector(gradients)
    num_parameters = parameters_values.shape[0]
    J_plus = np.zeros((num_parameters, 1))
    J_minus = np.zeros((num_parameters, 1))
    gradapprox = np.zeros((num_parameters, 1))
    
    # Compute gradapprox
    for i in range(num_parameters):
        
        # Compute J_plus[i]. Inputs: "parameters_values, epsilon". Output = "J_plus[i]".
        # "_" is used because the function you have to outputs two parameters but we only care about the first one
            # Step 1
        theta_plus = np.copy(parameters_values)
        theta_plus[i][0] += epsilon
            # Step 2
        J_plus[i],_ = forward_propagation_n(X,Y,vector_to_dictionary(theta_plus))
        
        
        # Compute J_minus[i]. Inputs: "parameters_values, epsilon". Output = "J_minus[i]".
        theta_minus = np.copy(parameters_values)
        theta_minus[i][0] -= epsilon
            # Step 2
        J_minus[i],_ = forward_propagation_n(X,Y,vector_to_dictionary(theta_minus))

        
        # Compute gradapprox[i]
        gradapprox[i] = (J_plus[i] - J_minus[i]) / (2*epsilon)
    
    # Compare gradapprox to backward propagation gradients by computing difference.
        # Step 1'
        numerator = np.linalg.norm(grad - gradapprox)
        
        # Step 2'
        denomoniator = np.linalg.norm(grad)+np.linalg.norm(gradapprox)
    
        # Step 3'
        difference = num_parameters / denomoniator
        

    if difference > 1e-7:
        print ("\033[93m" + "There is a mistake in the backward propagation! difference = " + str(difference) + "\033[0m")
    else:
        print ("\033[92m" + "Your backward propagation works perfectly fine! difference = " + str(difference) + "\033[0m")
    
    return difference