3. Deep Neural Network
深层神经网络(Deep L-layer neural network)
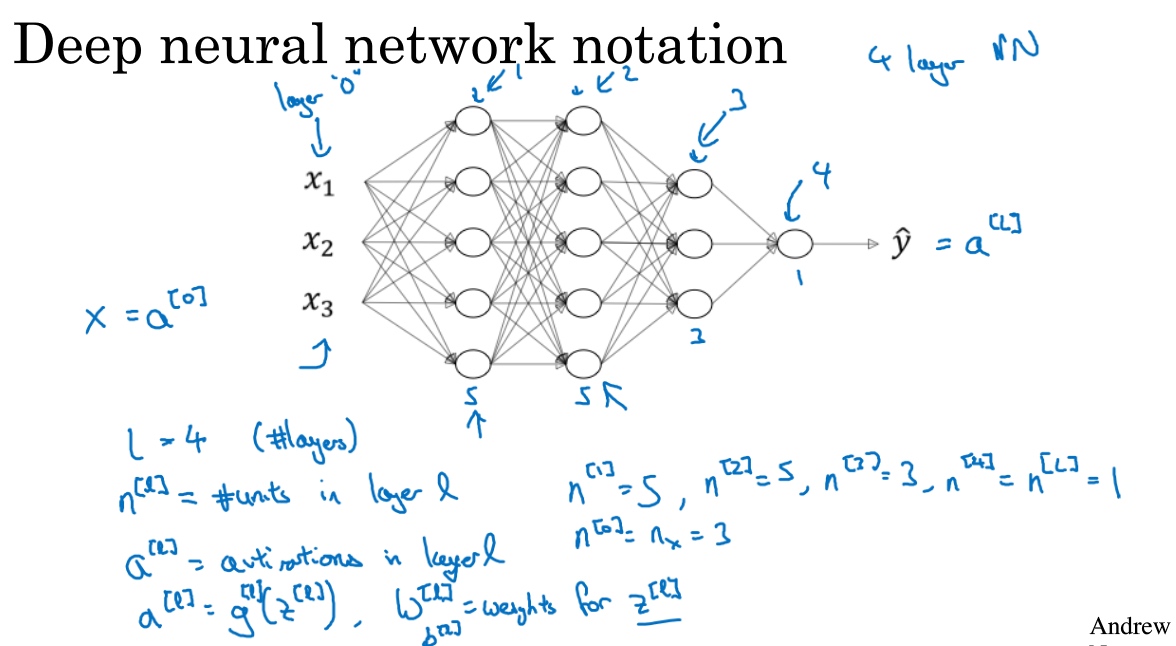
- L表示层数, 上图L=4
- $n^{[l]}$表示第$l$层的隐藏单元数, $E.g. \;n^{[1]}=5,n^{[3]}=3 $
- $a^{[l]}$来记作$l$层激活后结果, $a^{[l]} = g^{[l]}(z^{[l]})$ $E.g. \;a^{[0]}=3$
- $w^{[l]}$来记作$l$层计算$z^{[l]}$值的权重
深层网络中的前向传播(Forward propagation in a Deep Network)
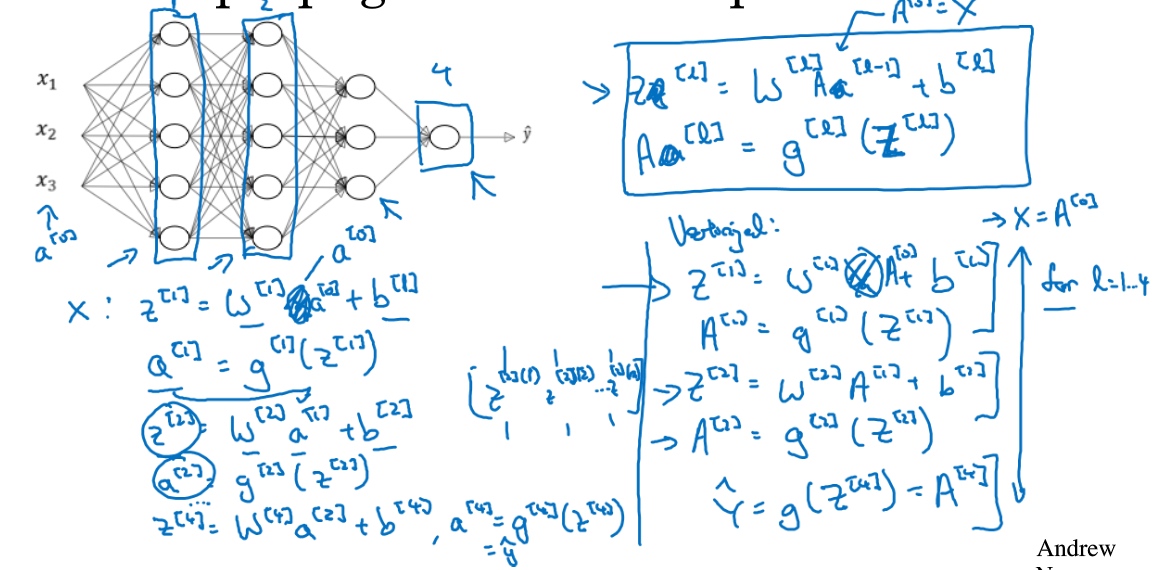
General forward propagation equation(vectorised):
$Z^{[l]}= W^{[l]}A^{[l-1]}+b^{[l]}$
$A^{[l]}=g^{[l]}(Z^{[l]})$
($A^{[0]}=X$)
核对矩阵的维数(Getting your matrix dimensions right)

Dimension of general equation:
$X^{[l]}: (n^{[l-1]},1)$
$W^{[l]}: (n^{[l]},n^{[l-1]})$
$b^{[l]}: (n^{[l]},1)$
$dw^{[l]}: (n^{[l]},n^{[l-1]})$
$db^{[l]}: (n^{[l]},1)$
For example:
$Z^{[1]}=W^{[1]}x+b^{[1]}$
$(3,1)\leftarrow (3,2) (2,1) + (3,1)$
$Z^{[2]}=W^{[2]}a^{[1]}+b^{[2]}$
$(5,1)\leftarrow (5,3) (3,1) + (5,1)$
多样本向量化:
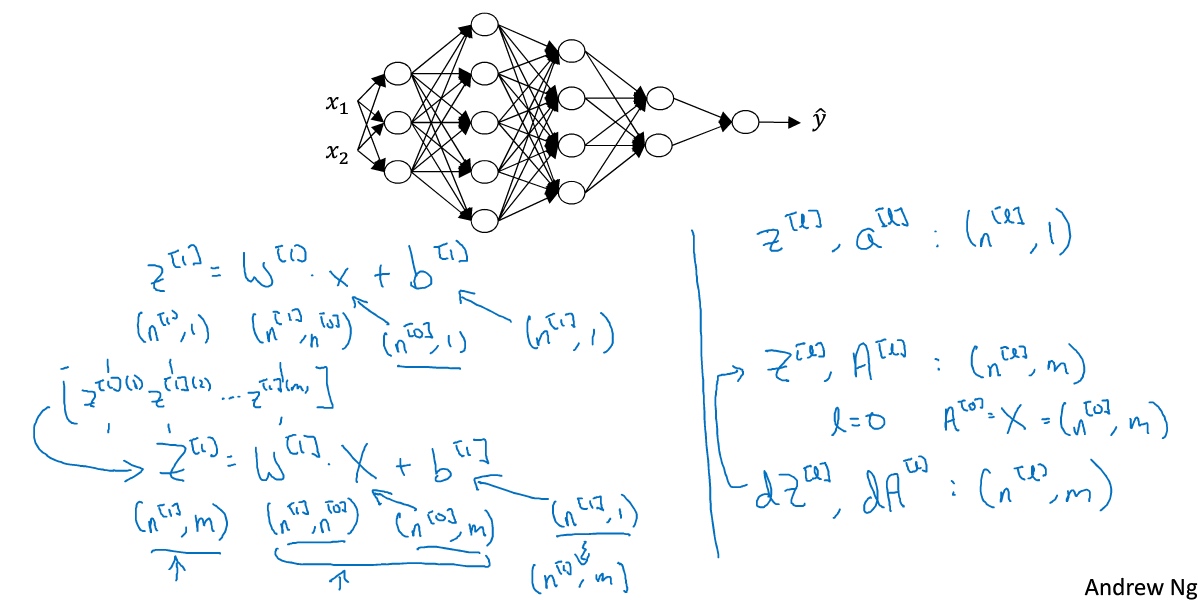
$Z^{[l}$可以看成由每一个单独的$z^{[l]}$叠加而得到, $Z^{[l}=(z^{[l][1]},z^{[l][2]},….,z^{[l][m]},)$
m为训练集大小, 所以$Z^{[l]}$的维度不再是$(n^{[l]},1)$,而是$(n^{[l]},m)$ $A^{[l}: (n^{[l]},m), A^{[0}=X=: (n^{[l]},m),$
为什么使用深层表示?(Why deep representations?)
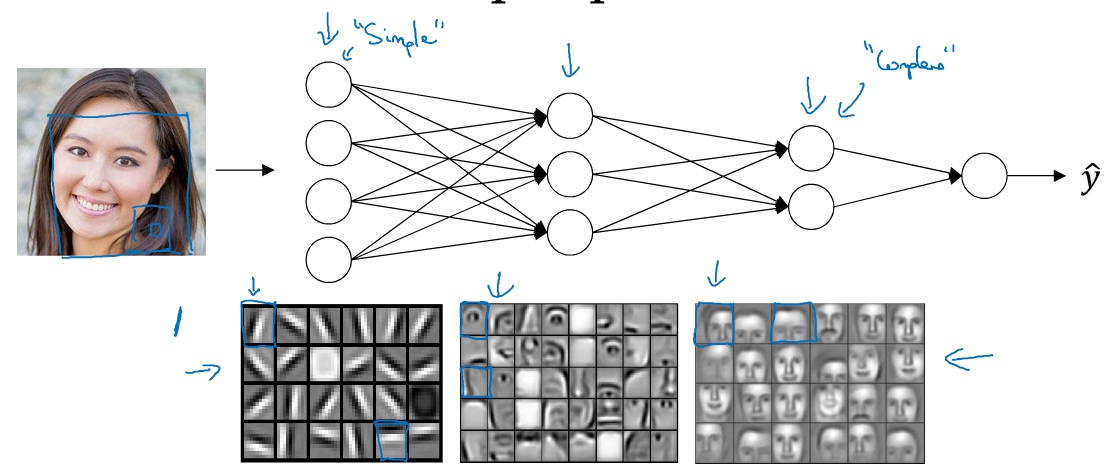
从简单的特征入手, 一步一步到更大更复杂的区域. 比如面部识别: 检测边缘 -> 器官识别 -> 面部识别

语音识别: 音位识别 -> 单词识别 -> 句子识别
Circuit theory and deep learning:
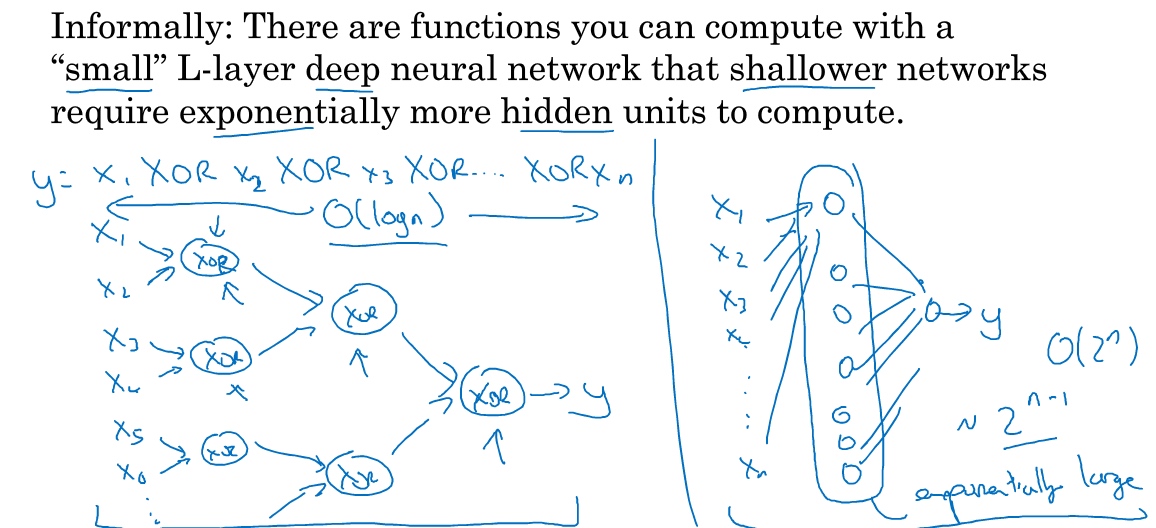
- 少隐藏单元, 多层数 ==> O(logn)
- 多隐藏单元(单元数目随输入比特指数上升), 少层数 ==> exponentially large (O(2^n))
总结:
- 深度神经网络的这许多隐藏层中,较早的前几层能学习一些低层次的简单特征,等到后几层,就能把简单的特征结合起来,去探测更加复杂的东西.
- 深层的网络隐藏单元数量相对较少,隐藏层数目较多,如果浅层的网络想要达到同样的计算结果则需要指数级增长的单元数量才能达到 ==> so called ‘deep learning’
搭建神经网络块(Building blocks of deep neural networks)
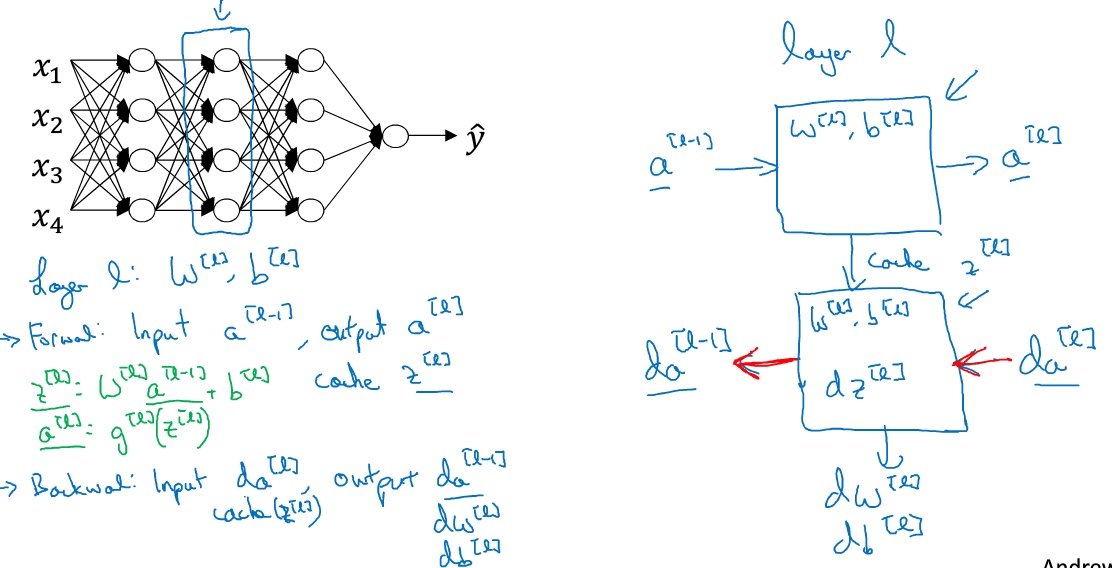
正向传播: 输入$a^{[l-1]}$, 输出是$a^{[l]}, a^{[l]}=g^{[l]}(z^{[l]})$, 缓存$z^{[l]}, z^{[l]}=W^{[l]}a^{[l-1]}+b^{[l]}$.
反向传播:
输入为$da^{[l]}$, 输出为$da^{[l-1]}$就会得到对激活函数的导数, 也就是希望的导数值$a^{[l]}$. $a^{[l-1]}$是会变的,前一层算出的激活函数导数。在第二个方块(上图)里需要$W^{[l]},b^{[l]}$,最后要算的是$dz^{[l]}$.然后第三个方块(上图)中,这个反向函数可以计算输出$dW^{[l]},db^{[l]}$。
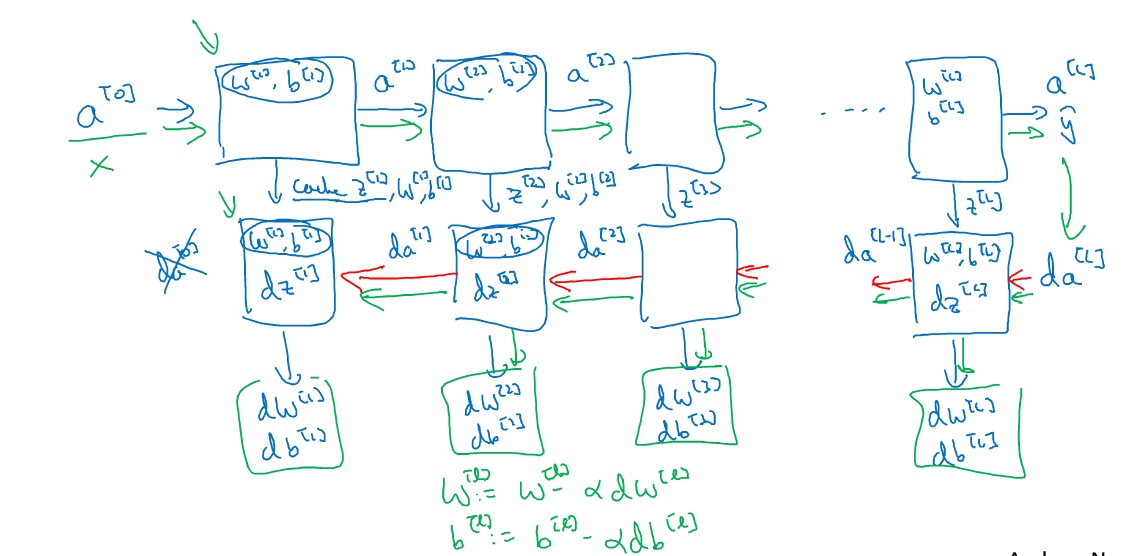
神经网络的计算过程:

前向传播和反向传播(Forward and backward propagation)

输入$a^{[l-1]}$, 输出是$a^{[l]}$, 缓存为$z^{[l]}$.
步骤:
$z^{[l]}=W^{[l]}a^{[l-1]}+b^{[l]}$
$a^{[l]}=g^{[l]}(z^{[l]})$
向量化:
$z^{[l]}=W^{[l]}A^{[l-1]}+b^{[l]}$
$A^{[l]}=g^{[l]}(Z^{[l]})$
反向传播:

输入为$da^{[l]}$, 输出为$da^{[l-1]},dw^{[l]},db^{[l]}$



参数VS超参数(Parameters vs Hyperparameters)

其他的超参数,如momentum、mini batch size、regularization parameters等等
参数: 人不可控制, 机器自主学习的参数
超参数: 仅人为可控的参数
hyper parameters determine(control) the final value of parameters, so it is called hyper parameter

如何寻找超参数的最优值?
走Idea—Code—Experiment—Idea这个循环,尝试各种不同的参数,实现模型并观察是否成功,然后再迭代
深度学习和大脑的关联性(What does this have to do with the brain?)
深度学习和大脑有什么关联性吗?
关联不大

深度学习的确是个很好的工具来学习各种很灵活很复杂的函数,学习到从x到y的映射,在监督学习中学到输入到输出的映射