神经网络概述和表示（Neural Network Overview and Representation）

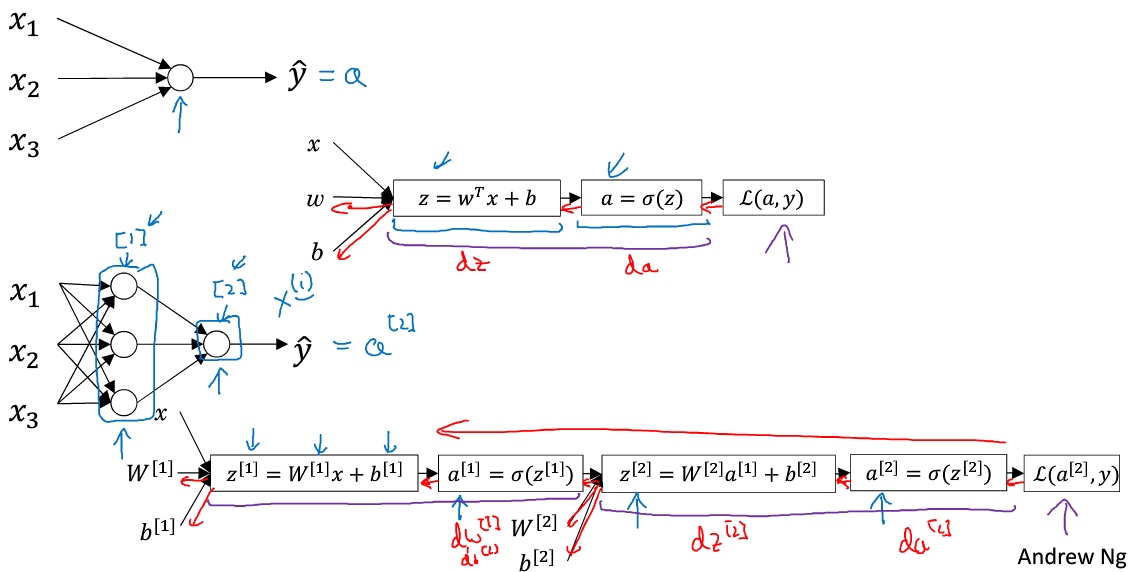
神经网络: 把许多sigmoid单元(hidden unit)堆叠起来形成一个神经网络。对首先通过公式$z=w^Tx+b$计算出值$z$，然后通过sigmoid函数$\sigma(z)$计算值$a$.

下面的神经网络只包含一个隐藏层.

输入层: 输入特征$x1,x2,x3$

隐藏层: 之所以叫隐藏层, 是因为中间节点的准确值是不知道的, 只能看到输入和输出值, 隐藏层中的东西再训练集中是无法看到的, 因此叫作隐藏层

输出层: 负责产生预测值

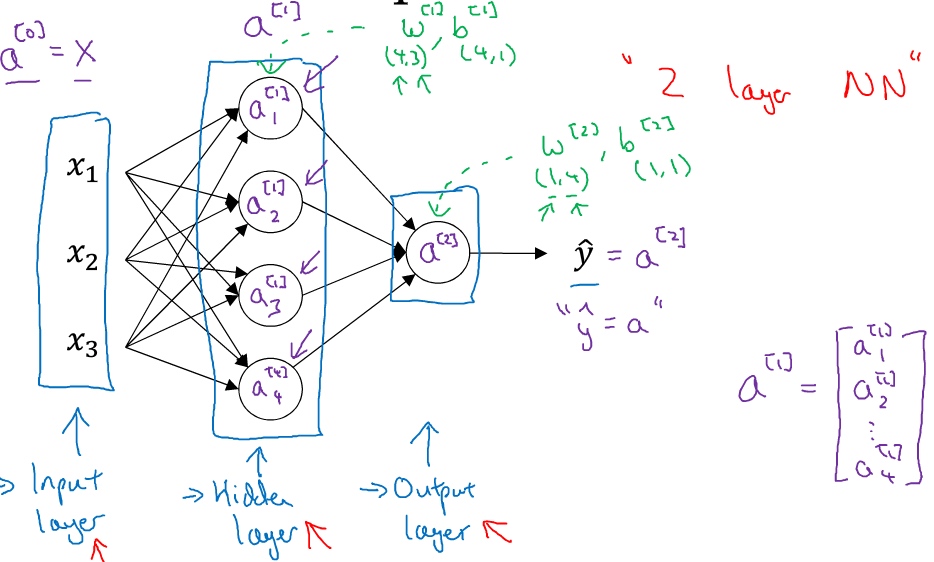
其中，x表示输入特征，a表示每个神经元的输出，W表示特征的权重，上标表示神经网络的层数（隐藏层为1），下标表示该层的第几个神经元。这是神经网络的符号惯例.

计算一个神经网络的输出（Computing a Neural Network’s output

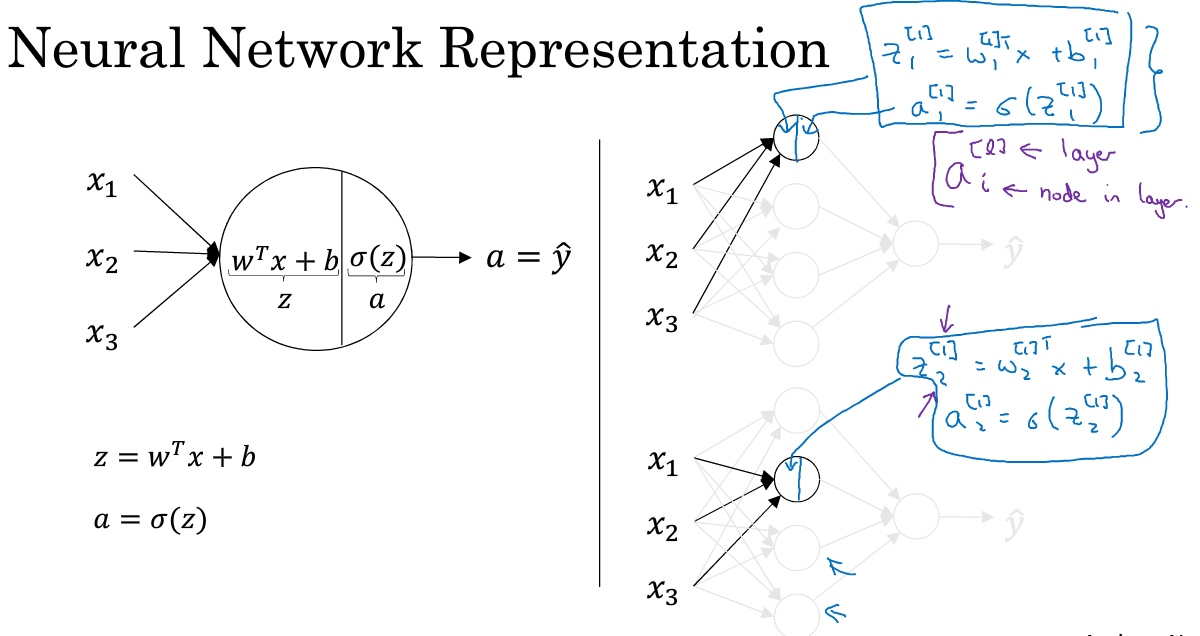
用圆圈表示神经网络的计算单元，逻辑回归的计算有两个步骤，首先你按步骤计算出z，然后在第二步中你以sigmoid函数为激活函数计算z（得出a），一个神经网络只是这样子做了好多次重复计算.

两层的神经网络中的第一层:

$z^{[1]}_1 = w_1^{[1]T}x + b^{[1]}_1,\; a^{[1]}_1 = \sigma(z^{[1]}_1)$

$z^{[1]}_2 = w_2^{[1]T}x + b^{[1]}_2,\; a^{[1]}_2 = \sigma(z^{[1]}_2)$

$z^{[1]}_2 = w_3^{[1]T}x + b^{[1]}_3,\; a^{[1]}_3 = \sigma(z^{[1]}_3)$

$z^{[1]}_4 = w_4^{[1]T}x + b^{[1]}_4,\; a^{[1]}_4 = \sigma(z^{[1]}_4)$

把这四个等式向量化, 向量化的过程:

将神经网络中的一层神经元参数纵向堆积起来，例如隐藏层中的w纵向堆积起来变成一个(4,3)的矩阵，用符号$W^{[1]}$表示

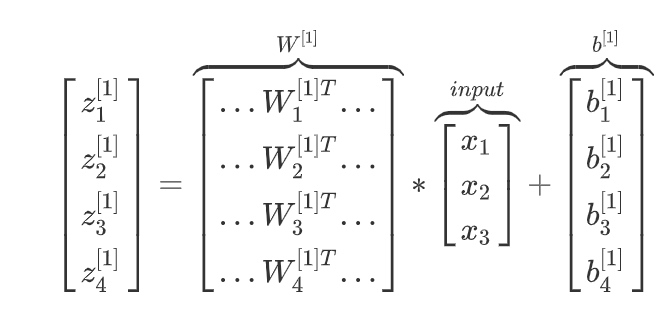
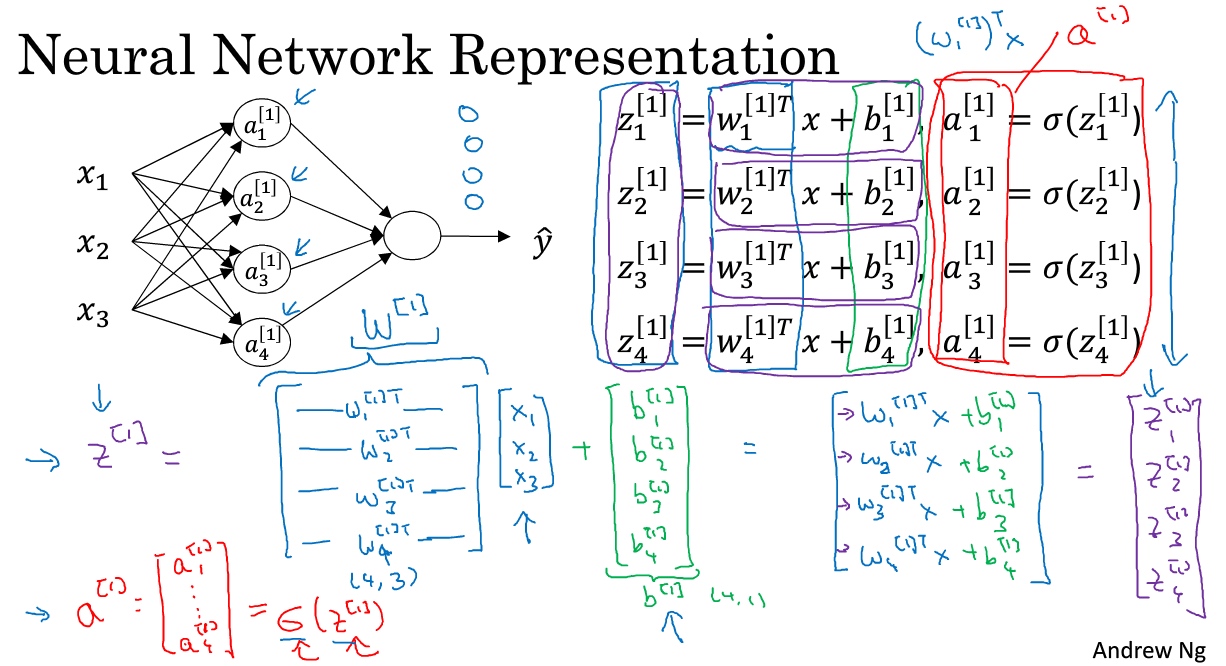
第一层的输入X, 可以用$a^{[0]}$表示, 而最一层的输出$\tilde{y}$可以用$a^{[2]}$表示

多样本向量化（Vectorizing across multiple examples）

神经网络的计算是所有的训练样本同时进行的:

上面的四个等式($z^{[1]},a^{[1]},z^{[2]},a^{[2]} $)可以计算出$a^{[2]}$等于$\tilde{y}$, 这是针对于单一的训练样本. 如果有个训练样本, 那么就需要重复这个过程(加了一个1到m的for循环).

向量化整个计算:

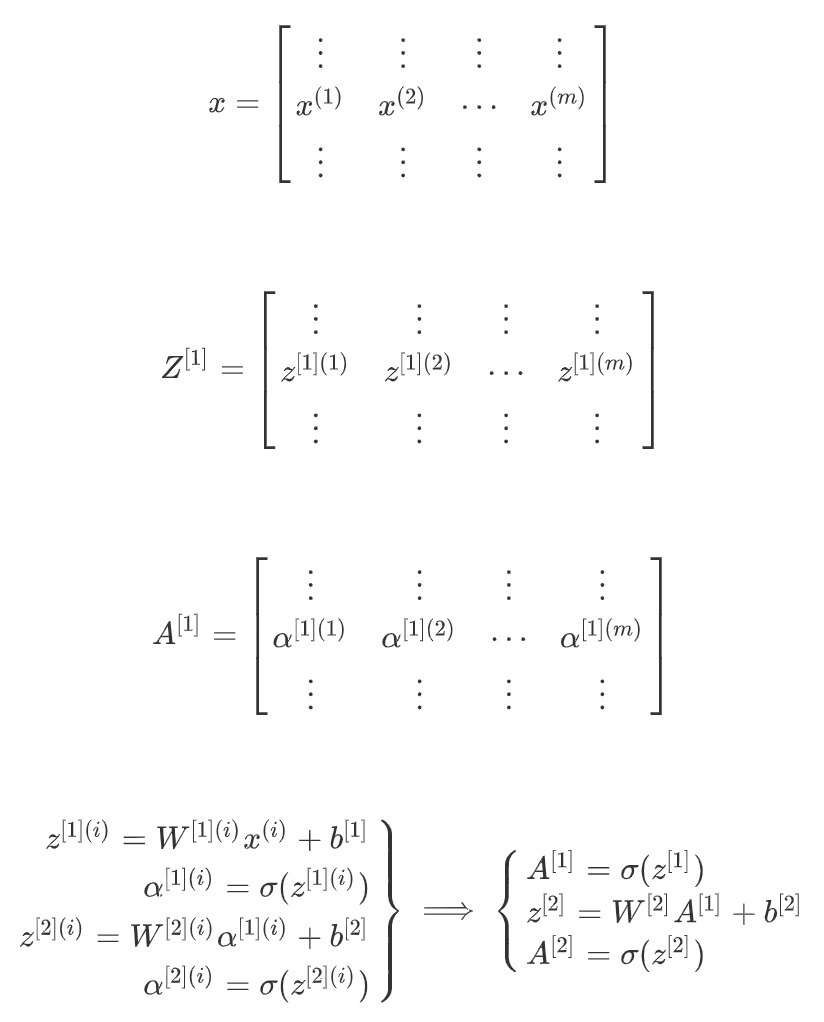
注: i是指第i个训练样本而[2]是指第二层隐藏层

• 从小写的向量x到这个大写的矩阵X，只是通过组合向量在矩阵的各列中。
• 同理，$z^{[1](1)},z^{[2](2)}$等等都是$z^{[1](m)}$的列向量，将所有都组合在各列中，就的到矩阵$Z^{[1]}$
• 同理，$a^{[1](1)},a^{[2](2)}$, …,$a^{[1](m)}$将其组合在矩阵各列中，就能得到矩阵$A^{[1]}$
• 同样的，对于$Z^{[2]}$和$A^{[2]}$，也是这样得到

一个矩阵中, 水平索引对应各个训练样本, 而垂直索引对应的是隐藏单元(神经网络中的不同节点).

向量化实现的解释（Justification for vectorized implementation）

激活函数（Activation functions）

使用一个神经网络时，需要决定使用哪种激活函数用隐藏层上，哪种用在输出节点上.

1. sigmoid函数, 值域[0,1]. $\sigma(z) = \frac{1}{1+e^{-z}}$
2. tanh函数/双曲正切函数, 值域[-1,1]. $tanh(z) = \frac{e^z - e^{-z}}{e^z + e^{-z}}$ 总体上都优于sigmoid函数的激活函数, 如果使用tanh函数代替sigmoid函数中心化数据，使得数据的平均值更接近0而不是0.5. 唯一例外是二分类问题中的输出层可以使用sigmoid函数.

sigmoid函数和tanh函数两者共同的缺点是，在z特别大或者特别小的情况下，导数的梯度或者函数的斜率会变得特别小，最后就会接近于0，导致降低梯度下降的速度.

1. ReLu函数(rectify linear unit)/修正线性单元的函数 $a=max(0,z)$ 只要z是正值的情况下，导数恒等于1，当是z负值的时候，导数恒等于0
2. Leaky Relu函数, 当z是负值时，这个函数的值不是等于0，而是轻微的倾斜. $a=max(0.01z,z)$

两者的优点是：

1. 在的区间变动很大的情况下，激活函数的导数或者激活函数的斜率都会远大于0
2. sigmoid和tanh函数的导数在正负饱和区的梯度都会接近于0，这会造成梯度弥散，而Relu和Leaky ReLu函数大于0部分都为常数，不会产生梯度弥散现象。(同时应该注意到的是，Relu进入负半区的时候，梯度为0，神经元此时不会训练，产生所谓的稀疏性，而Leaky ReLu不会有这问题)

z在ReLu的梯度一半都是0，但是，有足够的隐藏层使得z值大于0，所以对大多数的训练数据来说学习过程仍然可以很快.

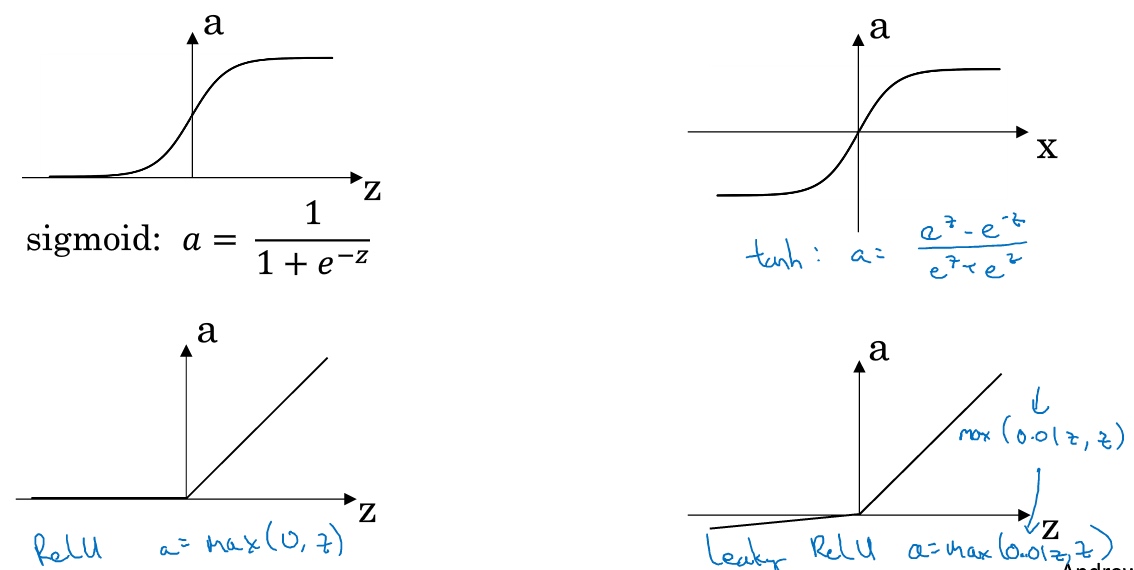
为什么需要非线性激活函数？（why need a nonlinear activation function?）

要让你的神经网络能够计算出有趣的函数，你必须使用非线性激活函数，证明如下：

去掉函数g，然后令$a^{[1]}=z^{[1]}$，或者也可以令$g(z)=z$，这个有时被叫做线性激活函数（更学术点的名字是恒等激励函数(Identity activation function)，因为它们就是把输入值输出）

如果改变前面的式子, 令

1. $a^{[1]}=z^{[1]} = W^{[1]}x+b^{[1]}$
2. $a^{[2]}=z^{[2]} = W^{[2]}a^{[1]}+b^{[2]}$ 将式子1代入式子2中, 则$a^{[2]}=z^{[2]} = W^{[2]}(W^{[1]}x+b^{[1]})+b^{[2]}$
3. $a^{[2]}=z^{[2]} = W^{[2]}W^{[1]}x+W^{[2]}b^{[1]}+b^{[2]}$ 简化多项式得到 $a^{[2]}=z^{[2]} = W^{\prime}x+b^{\prime}$ 如果是用线性激活函数(恒等激励函数)，那么神经网络只是把输入线性组合再输出

如果使用线性激活函数或者没有使用一个激活函数，那么无论神经网络有多少层一直在做的只是计算线性函数, 除非你引入非线性，否则你无法计算更有趣的函数.

激活函数的导数（Derivatives of activation functions）

1）sigmoid activation function

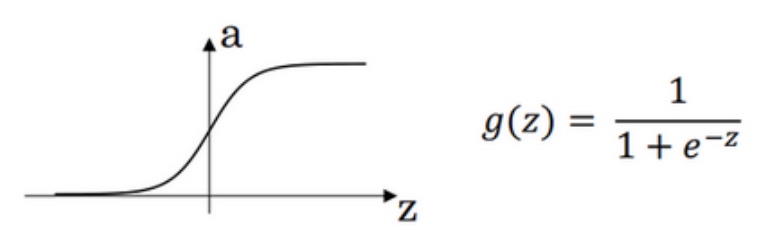
$\sigma(z) = \frac{1}{1+e^{-z}}$

$\frac{d}{dz}g(z) = \frac{1}{1-e^{-z}}(1-\frac{1}{1-e^{-z}}) = g(z)(1-g(z))$

注:

当z = 10 or -10时, $\frac{d}{dz}g(z) \approx 0$

当z = 0时, $\frac{d}{dz}g(z) = \frac{1}{2} -(1-\frac{1}{2}) = \frac{1}{4}$

2) Tanh activation function

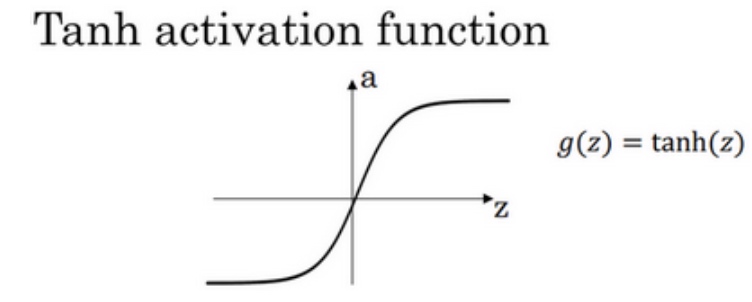
$tanh(z) = \frac{e^z - e^{-z}}{e^z + e^{-z}}$

$\frac{d}{dz}g(z) = 1 -(tanh(z))^2$

注:

当z = 10 or -10时, $\frac{d}{dz}g(z) \approx 0$

当z = 0时, $\frac{d}{dz}g(z) = 1 -(0) = 1$

3）Rectified Linear Unit (ReLU)

$g(z) = max(0, z)$

$$ g\prime(z)= \{ \begin{aligned} 0 \;\; if\;z<0\\ 1 \;\; if\;z>0\\\\ undefined \;\; if\;z=0\\ \end{aligned} $$

4）Leaky linear unit (Leaky ReLU)

$g(z) = max(0.01z, z)$

$$ g\prime(z)= \{ \begin{aligned} 0.01 \;\; if\;z<0\\ 1 \;\; if\;z>0\\\\ undefined \;\; if\;z=0\\ \end{aligned} $$

神经网络的梯度下降（Gradient descent for neural networks）

直观理解反向传播（Backpropagation intuition）

在逻辑回归中:

正向传播:

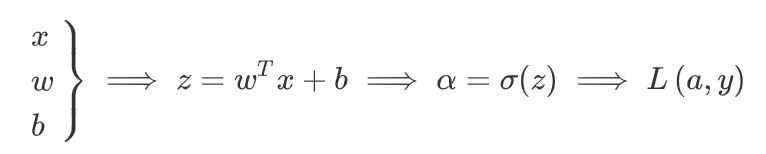
正向传播步骤，其中计算z，然后a，然后损失函数L.

反向传播:

在双层神经网络中:

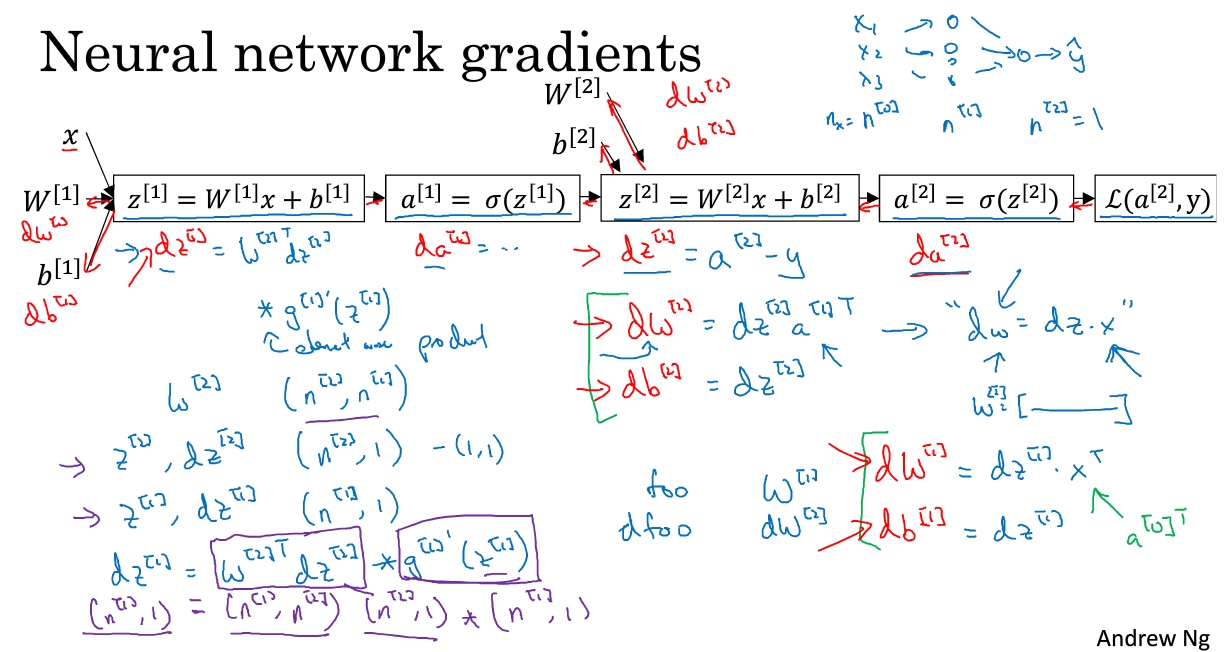
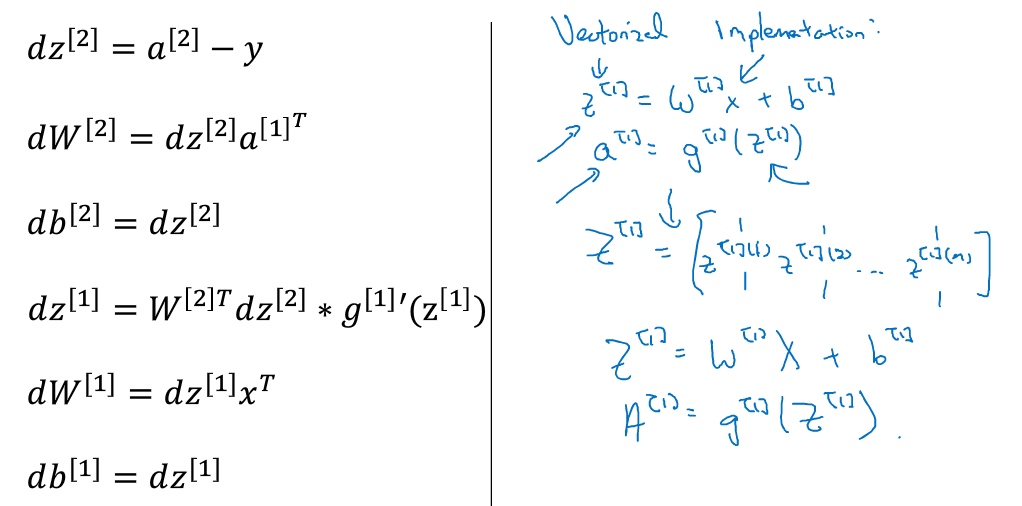
手推BP:

• https://mattmazur.com/2015/03/17/a-step-by-step-backpropagation-example/ (英)
• https://www.cnblogs.com/charlotte77/p/5629865.html (中)

随机初始化（Random Initialization）

对于逻辑回归，把权重初始化为0是可以的。但是对于一个神经网络，如果把权重或者参数都初始化为0，那么梯度下降将不会起作用.

把$W^{[1]}$初始化为0的2*2矩阵, 则$a^{[1]}_1和a^{[2]}_2$相等, 做反向传播计算时, $dz^{[1]}_1和dz^{[2]}_2$相等.

但是把偏置项b初始化为0是合理的.

如果这样初始化这个神经网络，那么这两个隐含单元就会完全一样，因此他们完全对称，也就意味着计算同样的函数，并且最终经过每次训练的迭代，这两个隐含单元仍然是同一个函数.

$dW$会是一个这样的矩阵，每一行有同样的值因此我们做权重更新把权重$W^{[1]} \Longrightarrow W^{[1]} - adW$每次迭代后的$W^{[1]}$，第一行等于第二行.

正确做法:

把$W^{[1]}$设为np.random.randn(2,2)(生成高斯分布)，通常再乘上一个小的数，比如0.01，这样把它初始化为很小的随机数。然后b没有这个对称的问题（叫做symmetry breaking problem），所以可以把b初始化为0，因为只要随机初始化W就有不同的隐含单元计算不同的东西，因此不会有symmetry breaking问题了。相似的，对于$W^{[2]}$你可以随机初始化，$b^{[2]}$可以初始化为0。

$W^{[1]} = np.random.randn(2,2) * 0.01, b^{[1]} = np.zeros((2,1))$

$W^{[2]} = np.random.randn(2,2) * 0.01, b^{[2]} = 0$

为什么是0.01, 而不是100或者1000?

通常倾向于初始化为很小的随机数。因为如果用tanh或者sigmoid激活函数, 如果（数值）波动太大，当计算激活值时如果W很大, z就会很大或者很小, 因此这种情况下很可能停在tanh/sigmoid函数的平坦的地方, 这些地方梯度很小也就意味着梯度下降会很慢, 因此学习也就很慢.