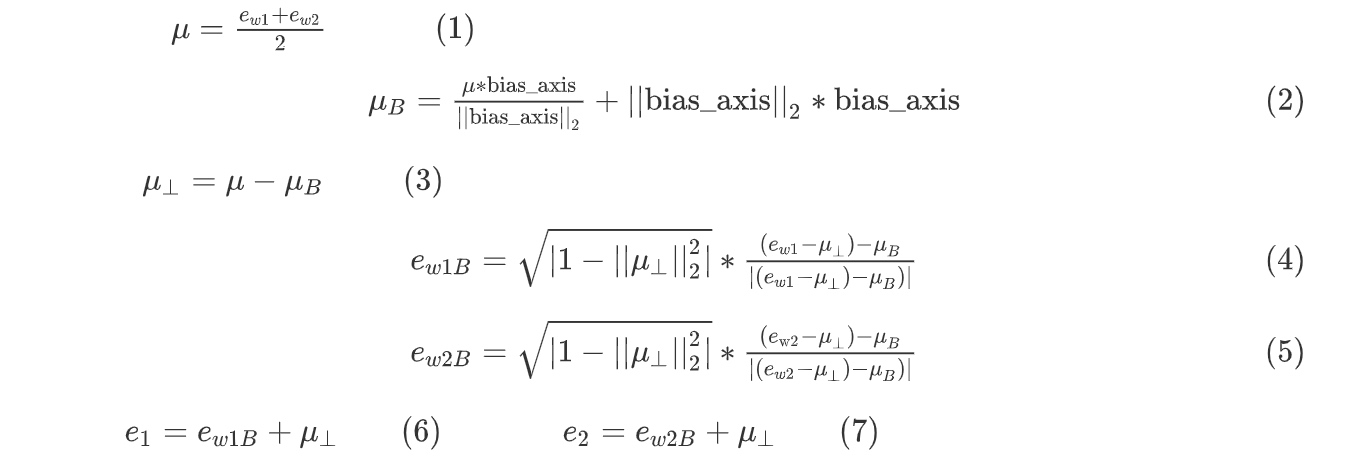词汇表征（Word Representation）

表征单词的一种方式是首先建立一个较大的词汇表（例如10000), 然后使用one-hot的方式对每个单词进行编码. 例如单词Man，Woman，King，Queen，Apple，Orange分别出现在词汇表的第5391，9853，4914，7157，456，6257的位置，则它们分别用$O_{5391},O_{9853},O_{4914},O_{7157},O_{456},O_{6257}$

(Weakness of one-hot representation is that it treats each word as a thing onto itself and it doesn’t allow algorithm easily generalize the cross words)

one-hot表征单词的方法最大的缺点就是每个单词都是独立的、正交的，无法知道不同单词之间的相似程度, 这样使得算法对相关词的泛化能力不强. 例如

“I want a glass of orange juice”

“I want a glass of apple ___”

Apple和Orange都是水果，词性相近，但是单从one-hot编码上来看，内积为零，算法无法知道二者的相似性. 在NLP中，我们更希望能掌握不同单词之间的相似程度

因此，可以使用特征表征（Featurized representation）的方法对每个单词进行编码. 也就是使用一个特征向量表征单词，特征向量的每个元素都是对该单词某一特征的量化描述，量化范围可以是[-1,1]之间. 特征表征的例子如下图所示：

特征向量的长度依情况而定，特征元素越多则对单词表征得越全面. 这里的特征向量长度设定为300. 使用特征表征之后，词汇表中的每个单词都可以使用对应的300 x 1的向量来表示(如上图编号1 所示), 该向量的每个元素表示该单词对应的某个特征值(即 与对应某个特征的相关程度). 每个单词用e和词汇表索引的方式标记，例如$e_{5391},e_{9853},e_{4914},e_{7157},e_{456},e_{6257}$

这种特征表征的优点是根据特征向量能清晰知道不同单词之间的相似程度，例如Apple和Orange之间的相似度较高，很可能属于同一类别。这种单词“类别”化的方式，大大提高了有限词汇量的泛化能力。这种特征化单词的操作被称为Word Embeddings，即单词嵌入。

值得一提的是，这里特征向量的每个特征元素含义是具体的，对应到实际特征，例如性别、年龄等。而在实际应用中，特征向量很多特征元素并不一定对应到有物理意义的特征，是比较抽象的. 但是，这并不影响对每个单词的有效表征，同样能比较不同单词之间的相似性。

每个单词都由高维特征向量表征，为了可视化不同单词之间的相似性，可以使用降维操作，例如t-SNE算法，将300D降到2D平面上. 如下图所示：

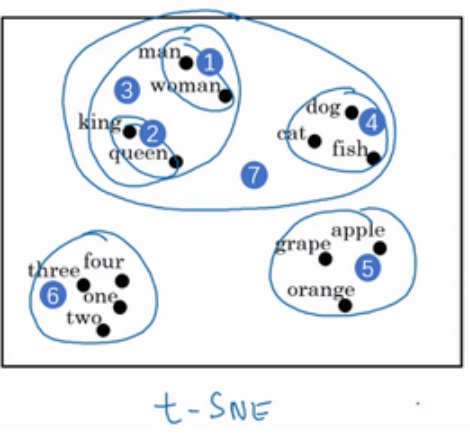
从上图可以看出相似的单词分布距离较近，从而也证明了Word Embeddings能有效表征单词的关键特征.

使用词嵌入（Using Word Embeddings）

在Named entity识别的例子中，每个单词采用的是one-hot编码. 如下图所示，因为’range farmer’是份职业，很明显’Sally Johnson’是一个人名.

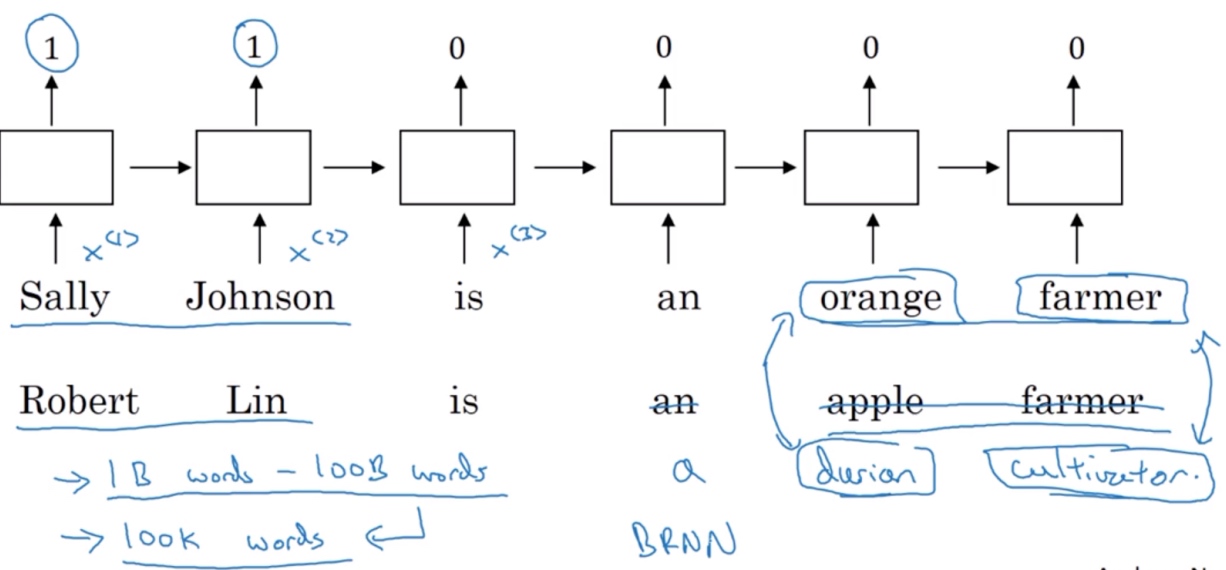
如果采用featurized representation对每个单词进行编码，再构建该RNN模型. 对于一个新的句子：

‘Robert Lin is an apple farmer’

由于这两个句子中, ‘apple’与’orange’特征向量很接近，很容易能判断出’Robert Lin’也是一个人名. 这就是featurized representation的优点之一.

可以看出，featurized representation的优点是可以减少训练样本的数目, 前提是对海量单词建立特征向量表述（word embedding), 即已经学好的词嵌入.

这样，即使训练样本不够多，测试时遇到陌生单词, 例如’durian cultivator’, 根据之前海量词汇特征向量就判断出’durian’也是一种水果，与’apple’类似, 而’cultivator’与’farmer’也很相. 从而归纳出与’durian cultivator”’对应的应该也是一个人名.

这种做法将单词用不同的特征来表示，即使是训练样本中没有的单词，也可以根据word embedding的结果得到与其词性相近的单词，从而得到与该单词相近的结果，有效减少了训练样本的数量.

featurized representation的特性使得很多NLP任务能方便地进行迁移学习. 词嵌入做迁移学习的步骤:

1. 从大量的文本集中学习word embeddings, 即所有单词的特征向量.
   • 或者从网上下载预训练好的word embeddings
2. 使用较少的训练样本, 将word embeddings迁移到新的任务中.
   • 这样就可以用更低维度的特征向量代替原来的10000维的one-hot向量
3. (optional)继续使用新数据微调word embeddings.
   • 建议仅当训练样本足够大的时候，再进行上述第三步.

当任务的训练集相对较小时，词嵌入的作用最明显，所以它广泛用于NLP领域(命名实体识别，文本摘要，文本解析, 指代消解, …)

有趣的是，word embeddings与人脸特征编码有很多相似性. 人脸图片经过Siamese网络，得到其特征向量f(x)，这点跟word embedding是类似的.

二者不同的是Siamese网络输入的人脸图片可以是数据库之外的(没有见过的照片), 神经网络都会计算出相应的一个编码结果; 而word embedding一般都是已建立的固定词汇库中的单词, 比如10000个单词，我们学习向量$e_1$到$e_{10000}$，学习一个固定的编码，每一个词汇表的单词的固定嵌入, 非词汇库单词统一用表示.

词嵌入的特性（Properties of Word Embeddings）

Word embeddings可以帮助找到不同单词之间的相似类别关系.

上例中, 特征维度是4维的，分别是[Gender, Royal, Age, Food]. 常识地, ‘Man’与’Woman’的关系类比于’King’与’Queen’的关系. 而利用Word embeddings可以自动找到这样的对应类比关系.

将’Man’的embedding vector与’Woman’的embedding vector相减：

类似地，将“King”的embedding vector与“Queen”的embedding vector相减：

相减结果表明，’Man’与’Woman’的主要区别是gender性别, ‘King’与’Queen’也是一样.

当算法被问及man对woman相当于king对什么时，算法所做的就是计算$e_{man} - e_{woman}$, 然后找出一个向量也就是找出一个词, 使得$e_{man} - e_{woman} \approx e_{king} - e_{?}$. 当这个新词是queen时，式子的左边会近似地等于右边

[Mikolov T, Yih W T, Zweig G. Linguistic regularities in continuous space word representations[J]. In HLT-NAACL, 2013.]

如上图所示，根据等式$e_{man}-e_{woman}\approx e_{king}-e_?$得： $e_?=e_{king}-e_{man}+e_{woman}$

利用相似函数，计算与$e_{king}-e_{man}+e_{woman}$相似性最大的$e_?$, 得到$e_?=e_{queen}$.

即,

$ \mathop{argmax}_{?}{ (e_{?}, e_{king}-e_{man}+e_{woman}) }$ 这种方法来做类比推理准确率大概只有30%~75%

关于相似函数, 比较常用的是cosine similarity. 其表达式为：

$Sim(u,v)=\frac{u^Tv}{||u||\cdot ||v||}$

(分子其实就是u和v的内积, 如果u和v非常相似，那么它们的内积将会很大)

把整个式子叫做余弦相似度，其实就是因为该式是u和v的夹角的余弦值. 如果向量u和v非常相似，它们的余弦相似性将接近1; 如果它们不相似，则余弦相似性将取较小的值

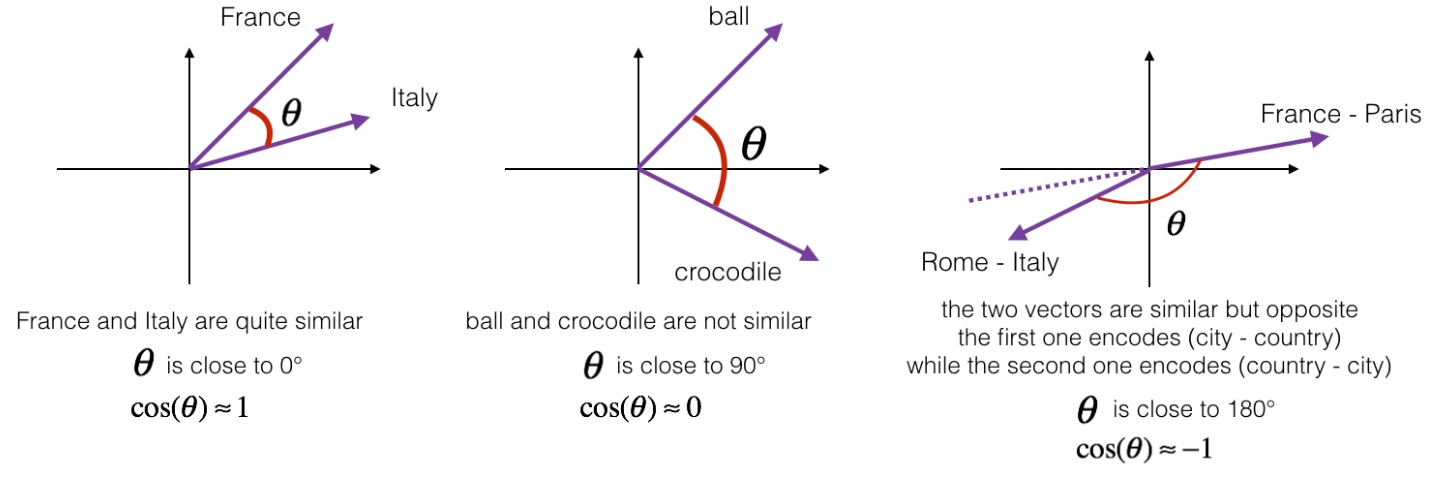
还可以计算Euclidian distance来比较相似性，即$||u-v||^2$. 距离越大，相似性越小.

嵌入矩阵（Embedding Matrix）

应用算法来学习词嵌入时，实际上是学习一个嵌入矩阵

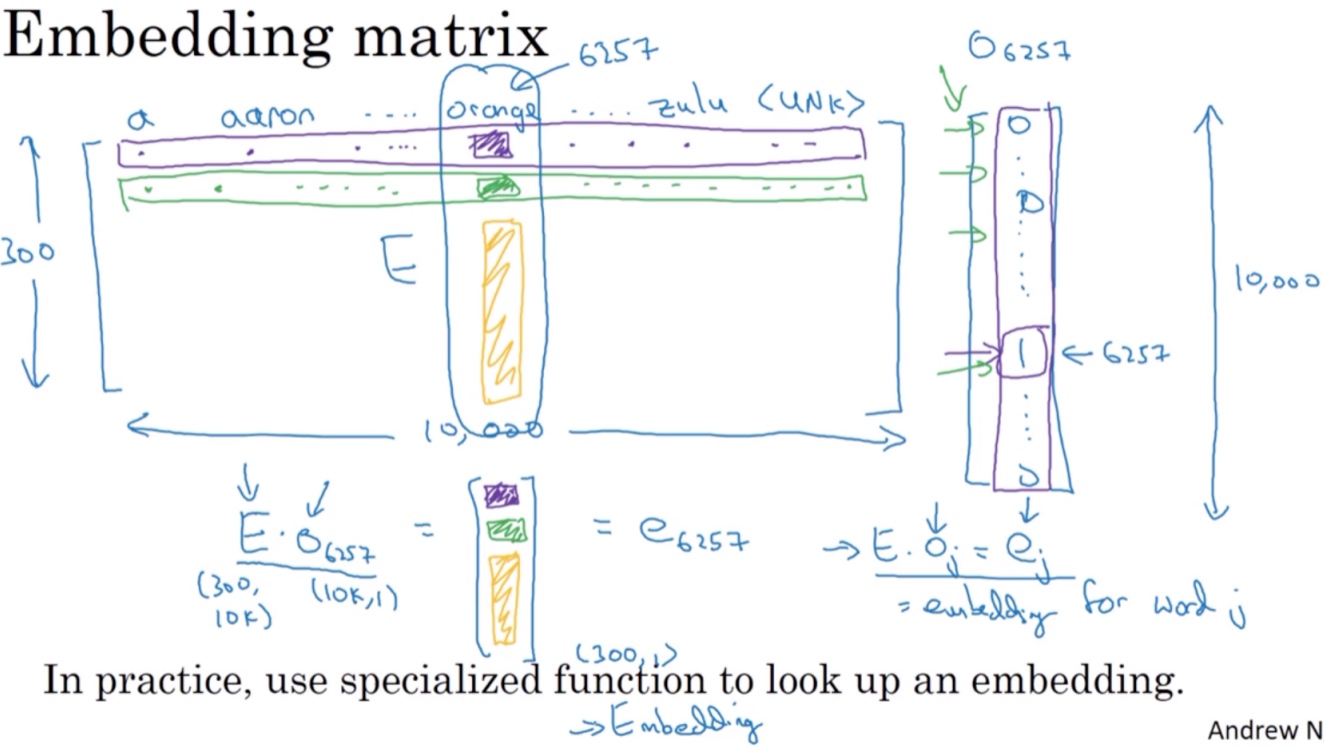
假设某个词汇库包含了10000个单词, 每个单词包含的特征维度为300, 那么表征所有单词的嵌入矩阵(embedding matrix)维度为(300 x 10000), 用E来表示. 某单词w的one-hot向量表示为$O_w$, 维度为(10000 x 1), 则该单词的嵌入向量(embedding vector)表达式为:

$e_w=E\cdot O_w$

因此，只要知道了嵌入矩阵E，就能计算出所有单词的嵌入向量$e_w$. 所以目标是学习一个嵌入矩阵, 随机地初始化矩阵, 然后使用梯度下降法来学习.

值得一提的是，上述这种矩阵乘积运算$E\cdot O_w$ 效率并不高，矩阵维度很大，且$O_w$大部分元素为零. 通常做法是直接从E中选取第w列作为$e_w$即可 (在Keras中就有一个嵌入层，然后我们用这个嵌入层更有效地从嵌入矩阵中提取出你需要的列，而不是对矩阵进行很慢很复杂的乘法运算).

学习词嵌入（Learning Word Embeddings）

嵌入矩阵E可以通过构建自然语言模型，运用梯度下降算法得到. 举个简单的例子，输入样本是下面这句话：

I want a glass of orange (juice).

通过这句话的前6个单词, 预测最后的单词’juice’.

嵌入矩阵E未知待求, 每个单词可用嵌入向量$e_w$表示, 构建的神经网络模型结构如下图所示：

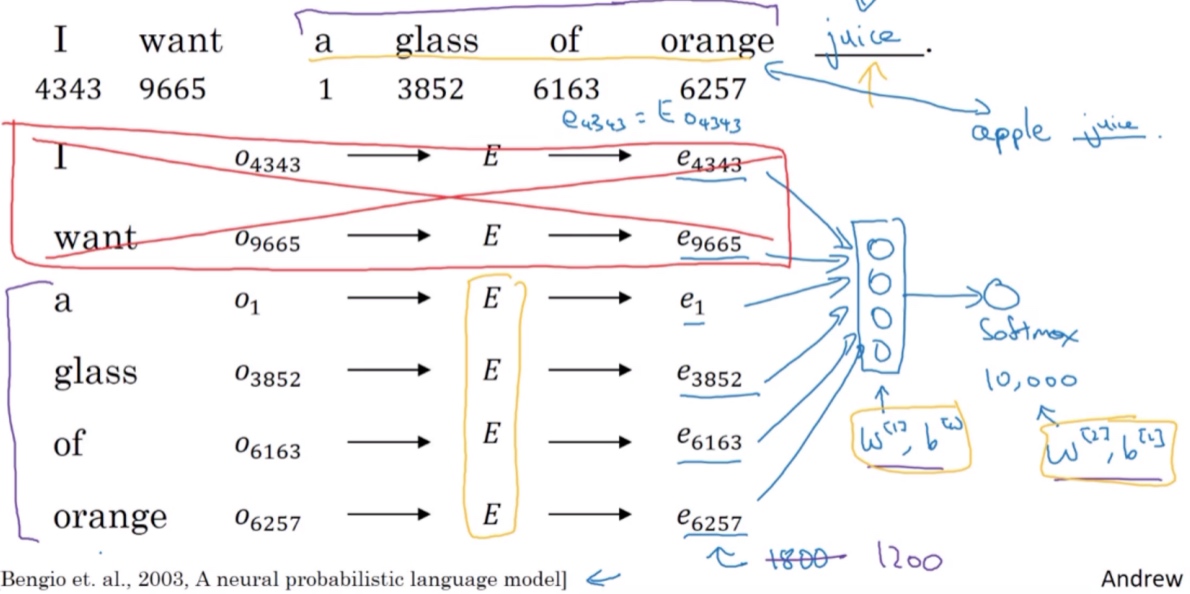
神经网络输入层包含6个嵌入向量, 每个嵌入向量维度是300, 则输入层总共有1800个输入. Softmax层有10000个概率输出 (与词汇表包含的单词数目一致), 目标就是预测出正确的输出标签’juice’. 其中, 隐藏层和softmax层有自己的参数与$E,W^{[1]},b^{[1]},W^{[2]},b^{[2]}$, 为待求值. 对足够的训练例句样本，运用梯度下降算法，迭代优化，最终求出embedding matrix E.

这种算法的效果还不错，能够保证具有相似属性单词的embedding vector相近.

为了让神经网络输入层数目固定(意味着可以处理任意长度的句子), 可以选择只取预测单词的前4个单词作为输入, 例如该句中只选择’a glass of orange’四个单词作为输入. 这里的4是超参数(可调). 神经网络会输入一个1200维的特征变量. 这个模型的参数就是嵌入矩阵E (所有的单词用的都是同一个矩阵E). 然后权重w,b也都是算法的参数, 用反向传播来进行梯度下降来最大化训练集似然，通过序列中给定的4个单词去重复地预测出语料库中下一个单词什么.

一般地，我们把输入叫做context，输出叫做target. 对应到上面这句话里：

• context: a glass of orange
• target: juice

关于context的选择有多种方法： - target前n个单词 (这个适合语言模型) - target前n个单词和后n个单词，n可调 - target前1个单词 - target附近某1个单词（Skip-Gram）

事实证明，不同的context选择方法都能计算出较准确的embedding matrix E.

Word2Vec

[Mikolov T, Chen K, Corrado G, et al. Efficient Estimation of Word Representations in Vector Space[J]. Computer Science, 2013]

通过Skip-Gram模型来选择context和target. 以下面这句话为例：

‘I want a glass of orange juice to go along with my cereal.’

Skip-Gram模型的做法是：首先随机选择一个单词作为context, 例如’orange’; 然后使用一个宽度为5或10(自定义)的滑动窗, 在context附近选择一个单词作为target, 可以是’juice’, ‘glass’,… 最终得到了多个context—target对作为监督式学习样本.

要解决的基本的监督学习问题是学习一种映射关系, 从上下文c (E.g. orange) 映射到 目标t (E.g. juice).

训练的过程是构建自然语言模型:

1. 输入上下文词orange的one-hot向量$O_c$
2. 拿嵌入矩阵E乘以向量$O_c$, 得到输入的上下文词的嵌入向量$e_c \;\; (e_c = E \cdot O_c)$
3. 把向量$e_c$喂入一个softmax单元, 经过softmax单元的输出为： $\hat y = p(t|c)=\frac{e^{\theta_t^T\cdot e_c}}{\sum_{j=1}^{10000}e^{\theta_j^T\cdot e_c}} $

其中，$\theta_t$为target对应的参数(即某个词t和标签相符的概率是多少); softmax中的偏差项被省略, 可加

相应的loss function为：

$L(\hat y,y)=-\sum_{i=1}^{10000}y_ilog\ \hat y_i$

然后，运用梯度下降算法，迭代优化，最终得到embedding matrix E

然而，这种算法计算量大，影响运算速度。主要因为softmax输出单元为10000个，$\hat y $计算公式中包含了大量的求和运算. 解决的办法之一是使用hierarchical softmax classifier，即树形分类器. 其结构如下图所示：

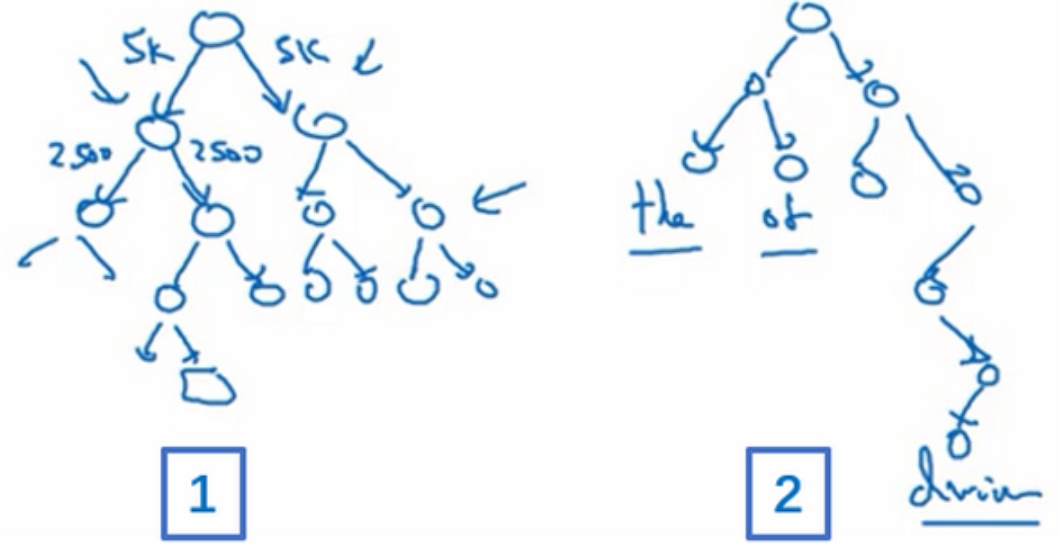
这种树形分类器是一种二分类. 与之前的softmax分类器不同，它在每个数节点上对目标单词进行区间判断，最终定位到目标单词. 这种树形分类器最多需要$log\ N$步就能找到目标单词，N为单词总数.

实际应用中，对树形分类器做了一些改进 (如编号2所示). 改进后的树形分类器是非对称的，通常选择把比较常用的单词 (a, the, of,…)放在树的顶层，而把不常用的单词放在树的底层 (durian, ..). 这样更能提高搜索速度.

最后一点，一旦你对上下文c进行采样，那么目标词t就会在上下文c的正负10个词距内进行采样, 但是你要如何选择上下文c？

关于context的采样，需要注意的是如果使用均匀随机采样，那么一些常用的介词、冠词，例如the, of, a, and, to等出现的概率更大一些. 但是，这些单词的embedding vectors通常不是我们最关心的，我们更关心例如orange, apple, juice等这些名词等. 所以，实际应用中，一般不选择随机均匀采样的方式来选择context，而是采用了不同的分级来平衡更常见的词和不那么常见的词.

Skip-Gram模型是Word2Vec的一种, Word2Vec的另外一种模型是连续词袋模型CBOW（Continuous Bag of Words), 它获得中间词两边的的上下文，然后用周围的词去预测中间的词，这个模型也很有效，也有一些优点和缺点.

CBOW是从原始语句推测目标字词；而Skip-Gram正好相反，是从目标字词推测出原始语句. CBOW对小型数据库比较合适，而Skip-Gram在大型语料中表现更好

右图为CBOW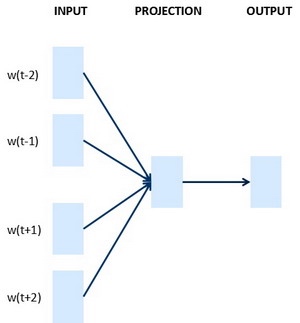

右图为Skip-Gram

负采样（Negative Sampling）

[Mikolov T, Sutskever I, Chen K, et al. Distributed Representations of Words and Phrases and their Compositionality[J]. 2013, 26:3111-3119.]

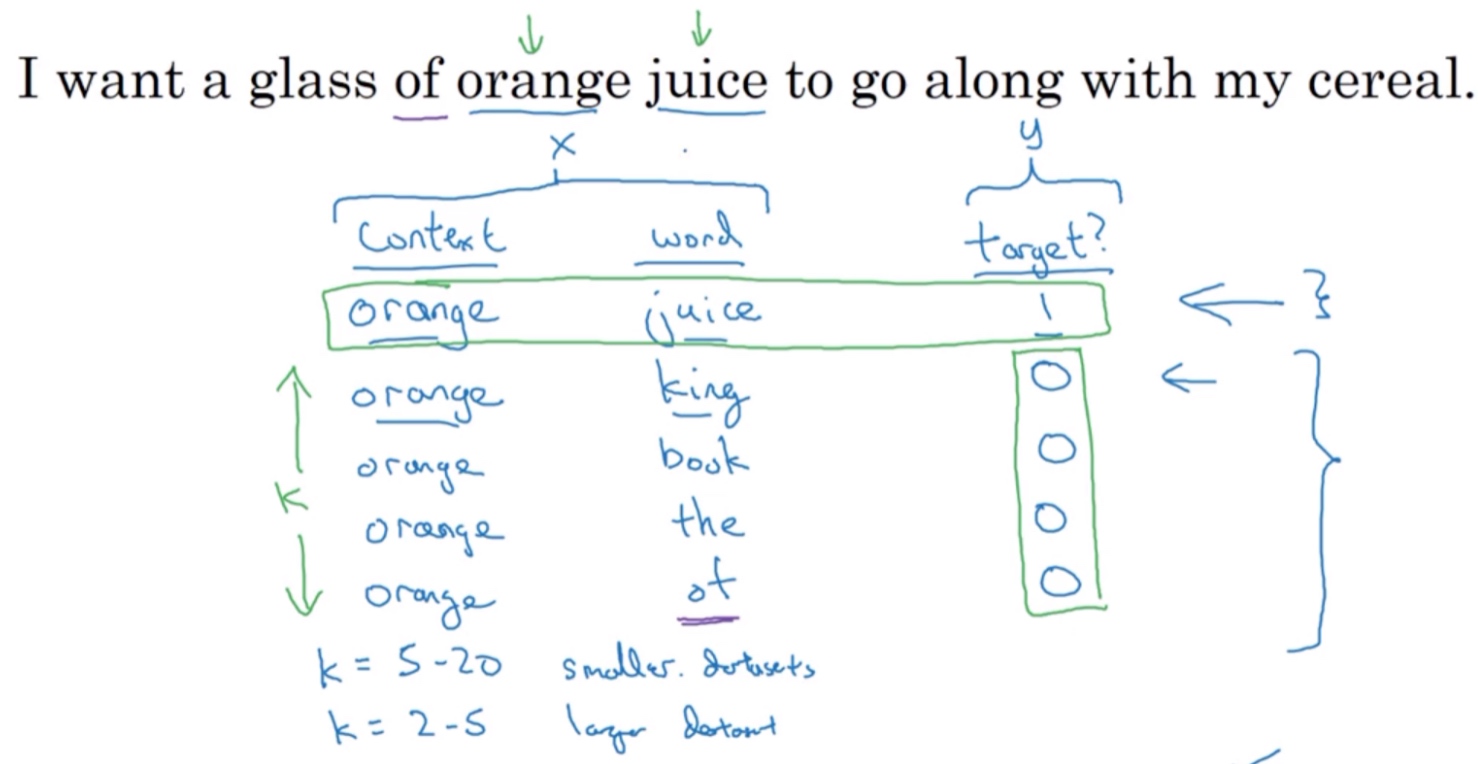
Negative sampling是另外一种有效的求解embedding matrix E的方法. 它的做法是判断选取的context word和target word是否构成一组正确的context-target对, 一般包含一个正样本和k个负样本. 例如, ‘orange’为context word，’juice’为target word, 很明显’orange juice’是一组context-target对，为正样本，相应的target label为1. 若’orange’为context word不变，target word随机选择’king, book, the, of’等. 这些都不是正确的context-target对，为负样本，相应的target label为0。一般地，固定某个context word对应的负样本个数k一般遵循:

• 若训练样本较小，k一般选择5～20
• 若训练样本较大，k一般选择2～5即可

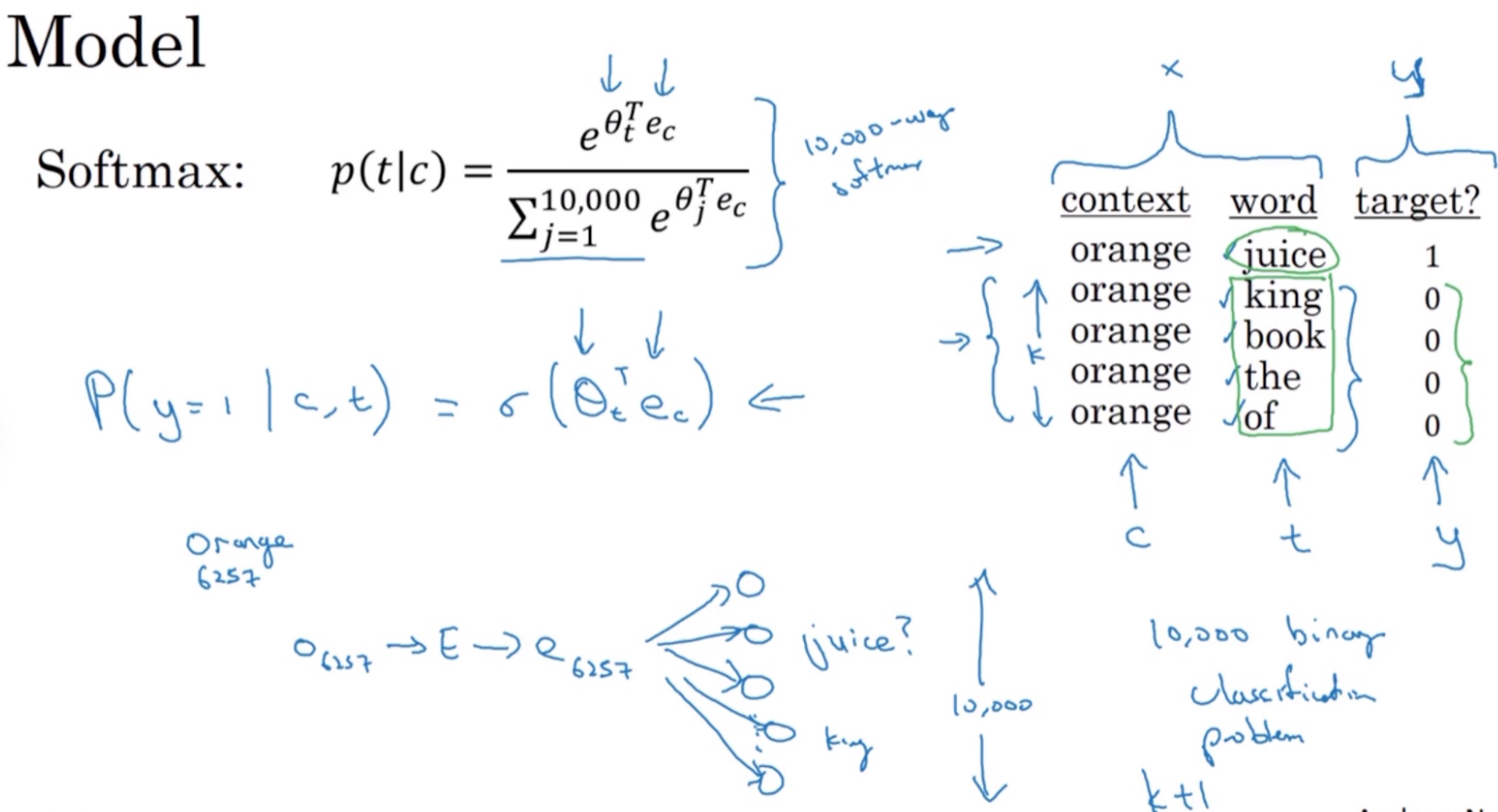
Negative sampling的数学模型为：

$P(y=1|c,t)=\sigma(\theta^T_t\cdot e_c)$ 其中，$\sigma$表示sigmoid激活函数, $\theta_t$是参数向量, $e_c$是上下文词的嵌入向量

很明显，negative sampling某个固定的正样本对应k个负样本，即模型总共包含了k+1个binary classification. 对比之前介绍的10000个输出单元的softmax分类，negative sampling转化为k+1个二分类问题，计算量要小很多，大大提高了模型运算速度.

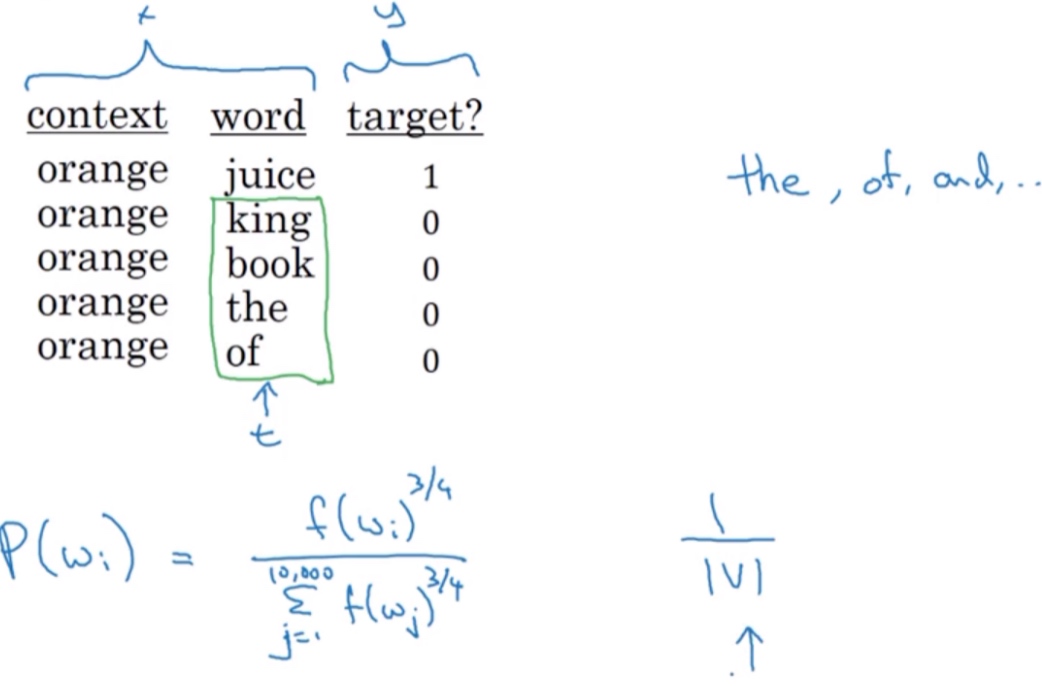
最后提一点，关于如何选择负样本对应的target单词，可以根据其在语料中的经验频率进行采样(通过词出现的频率对其进行采样). 但是在like、the、of、and诸如此类的词上有很高的频率.

论文的作者Mikolov等人根据经验提出一个更实用、效果更好的方法，就是根据该词出现的频率进行选择，相应的概率公式为：

$P(w_i)=\frac{f(w_i)^{\frac34}}{\sum_j^{10000}f(w_j)^{\frac34}}$ 其中，$f(w_i)$表示单词$w_i$在单词表中出现的概率(词频),通过$\frac{3}{4}$次方的计算，使其处于完全独立的分布和训练集的观测分布两个极端之间

最后还是建议下载别人预训练过的词向量

GloVe 词向量（GloVe Word Vectors）

[Pennington J, Socher R, Manning C. Glove: Global Vectors for Word Representation[C]// Conference on Empirical Methods in Natural Language Processing. 2014:1532-1543.]

在Word2Vec中, 通过挑选语料库中位置相近的两个词, 列举出词对, 即上下文和目标词, GloVe算法做的就是使其关系开始明确化.

GloVe算法引入了一个新的参数:

• $X_{ij}$: 表示单词i出现在单词j之前的次数, 即i和j同时出现的次数
  • 其中，i表示context，j表示target
  • 一般地，如果不限定context一定在target的前面，则有对称关系$X_{ij}=X_{ji}$
  • 如果有限定先后，则$X_{ij}\neq X_{ji}$接下来的讨论中，我们默认存在对称关系$X_{ij}=X_{ji}$
  • ($X_{ij}$就是一个能够获取单词i和单词j出现位置相近时或是彼此接近的频率的计数器)

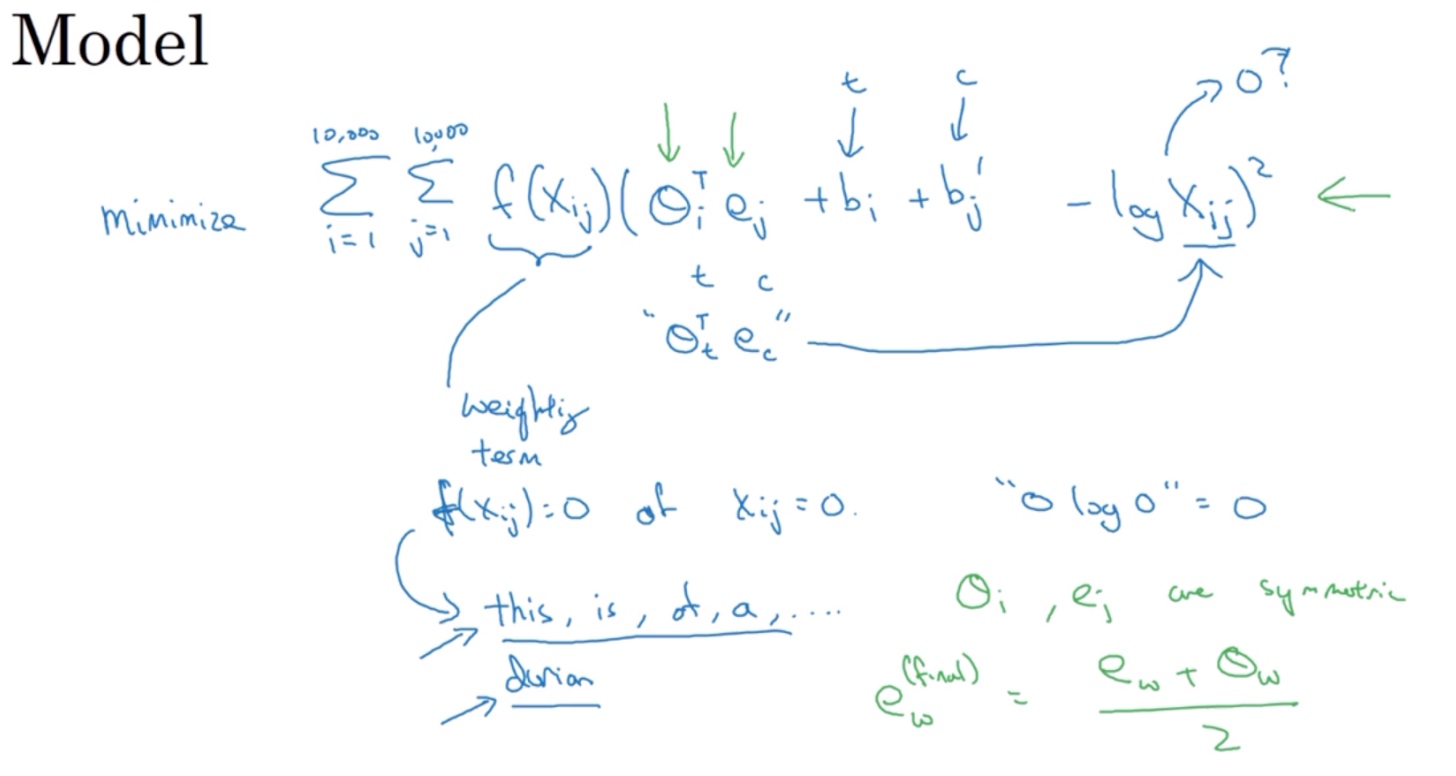
GloVe模型的loss function为:

$L=\sum_{i=1}^{10000}\sum_{j=1}^{10000}(\theta_i^Te_j-log X_{ij})^2$

两个单词之间有多少联系, 就是他们同时出现的频率是多少，这是由这个$X_{ij}$影响的.

从上式可以看出，若两个词的embedding vector越相近，同时出现的次数越多，则对应的loss越小.

为了防止出现’log 0’, 即两个单词不会同时出现$X_{ij}=0$ (无相关性的情况), 对loss function引入一个权重因子$f(X_{ij})$:

$$L=\sum_{i=1}^{10000}\sum_{j=1}^{10000}f(X_{ij})(\theta_i^Te_j-log X_{ij})^2$$

当$X_{ij}=0$时，权重因子$f(X_{ij})=0$. (即$0log0= 0$，这个的意思是如果$X_{ij}=0$，先不要进行求和，所以这个’log 0’项就是不相关项). 这种做法直接忽略了无任何相关性的context和target，只考虑$X_{ij} \gt 0$的情况.

出现频率较大的单词(this，is，of，a)相应的权重因子$f(X_{ij})$较大但不至于过分，出现频率较小的单词(durion)相应的权重因子$f(X_{ij})$较小一些但不至于太小. 具体的权重因子$f(X_{ij})$选取方法可查阅篇头论文.

一般地，引入偏移量，则loss function表达式为：

$$L=\sum_{i=1}^{10000}\sum_{j=1}^{10000}f(X_{ij})(\theta_i^Te_j+b_i+b_j’-log X_{ij})^2$$

值得注意的是，参数$\theta_i$和$e_j$是对称的(他们的功能相近). 因此一种训练算法的方法是一致地初始化$\theta , e$，然后使用梯度下降来最小化输出，当每个词都处理完之后取平均值，最后给定一个词w, 就会得到:

$$e_w^{final}=\frac{e_w+\theta_w}{2}$$

最后提一点的是，无论使用Skip-Gram模型还是GloVe模型等等，计算得到的embedding matrix E的每一个特征值不一定对应有实际物理意义的特征值，如gender，age等. 某个特征可能是特征可能是个Gender、Roya、Age、Food Cost和Size的组合, 它也许是名词或是一个行为动词和其他所有特征的组合.

尽管存在特征量潜在的任意线性变换，但是最终还是能学习出解决类似问题的平行四边形映射.

情感分类（Sentiment Classification）

情感分类一般是根据一句话来判断其喜爱程度，例如1～5星分布. 如下图所示：

情感分类问题的一个主要挑战是缺少足够多的训练样本. 而Word embedding恰恰可以帮助解决训练样本不足的问题. 有了词嵌入，即使只有中等大小的标记的训练集，你也能构建一个不错的情感分类器.

首先介绍使用word embedding解决情感分类问题的一个简单模型算法.

如上图所示，这句话的4个单词分别用embedding vector表示. $e_{8928},e_{2468},e_{4694},e_{3180}$, 然后经过平均值计算单元计算均值，这样得到的平均向量的维度仍是300. 最后经过softmax输出1～5星. 这种模型结构简单，计算量不大，不论句子长度多长，都使用平均的方式得到300D的embedding vector. 该模型实际表现较好.

但是，这种简单模型的缺点是使用平均方法，没有考虑句子中单词出现的次序，忽略其位置信息. 而有时候，不同单词出现的次序直接决定了句意，即情感分类的结果. 例如下面这句话：

• Completely lacking in good taste, good service, and good ambience.

虽然这句话中包含了3个’good’, 但是其前面出现了’lacking’, 很明显这句话句意是negative的. 如果使用上面介绍的平均算法，则很可能会错误识别为positive的，因为忽略了单词出现的次序 (‘good’出现了3次).

为了解决这一问题，情感分类的另一种模型是RNN:

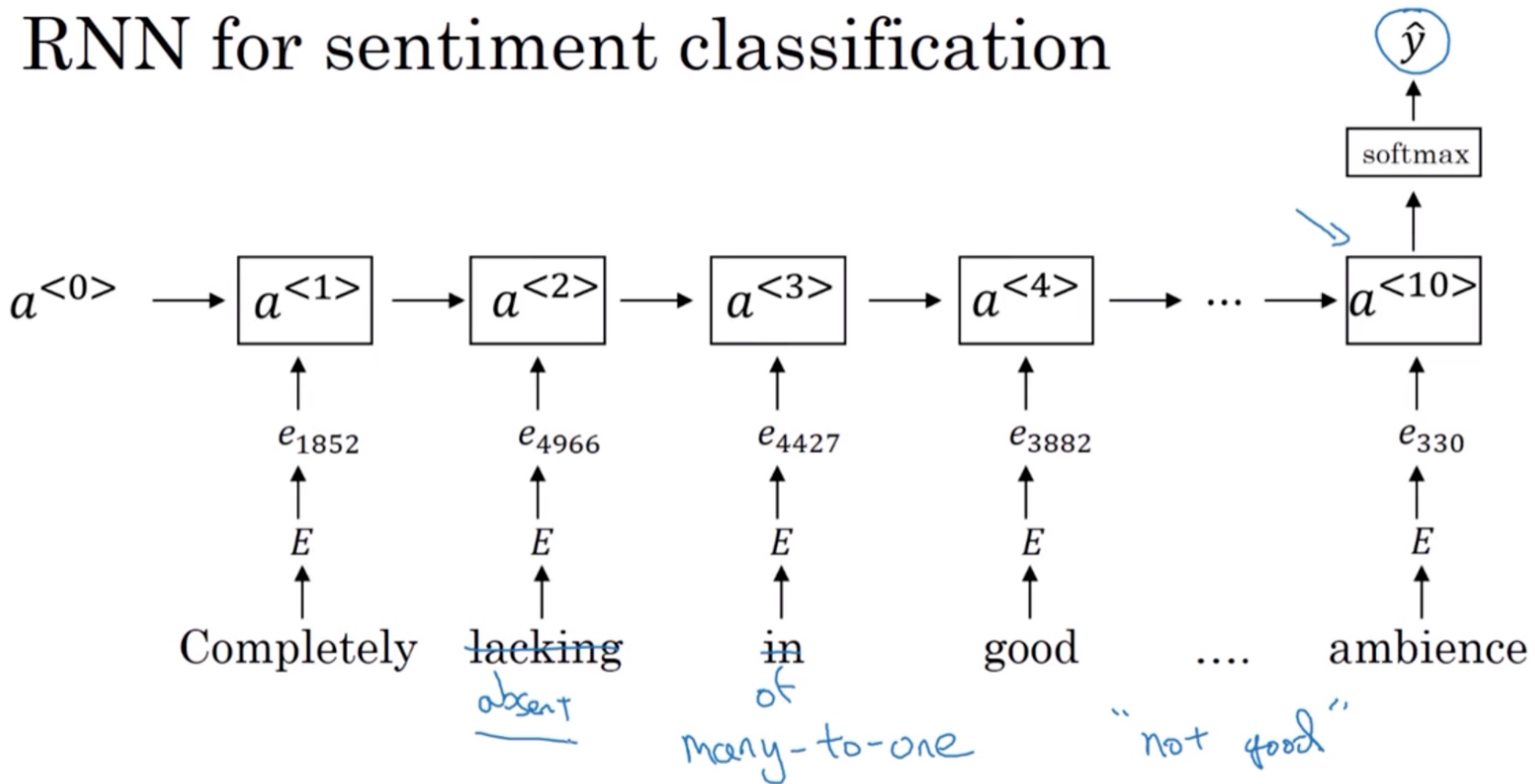
用每一个one-hot向量乘以词嵌入矩阵E，得到词嵌入表达e，然后把它们送进RNN里. RNN的工作就是在最后一步计算一个特征表示，用来预测$\tilde{y}$. 该RNN模型是典型的many-to-one模型，考虑单词出现的次序，能够有效识别句子表达的真实情感.

值得一提的是由于词嵌入是在一个更大的数据集里训练的，能够有效提高模型的泛化能力，即使训练样本不多，也能保证模型有不错的性能

词嵌入除偏（Debiasing Word Embeddings）

现在机器学习和人工智能算法正渐渐地被信任用以辅助或是制定极其重要的决策，因此我们想尽可能地确保它们不受非预期形式偏见影响.

Word embeddings中存在一些性别、宗教、种族等偏见(bias)或者歧视. 例如下面这3句话：

• Man: Woman as King: Queen
• Man: Computer programmer as Woman: Homemaker
• Father: Doctor as Mother: Nurse

很明显，第二句话和第三句话存在性别偏见，因为Woman和Mother也可以是Computer programmer和Doctor.

以性别偏见为例，我们来探讨下如何消除word embeddings中偏见.

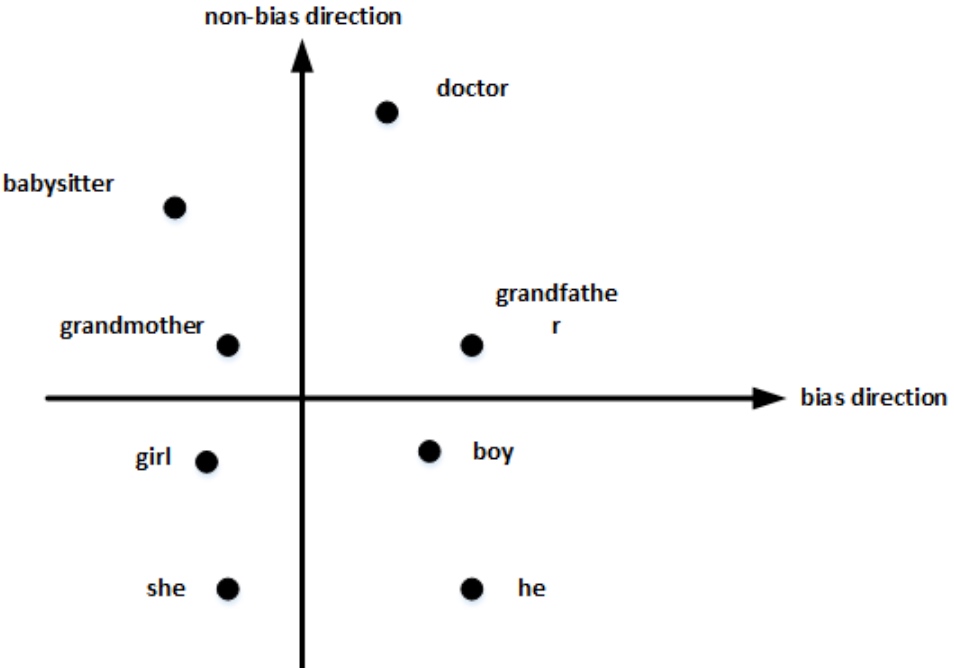
首先，确定偏见bias的方向. 方法是对所有性别对立的单词求差值, 再平均. 上图展示了bias direction和non-bias direction. 偏见趋势可以将它看做1D子空间，无偏见趋势就会是299D的子空间

$$bias\ direction=\frac1N ((e_{he}-e_{she})+(e_{male}-e_{female})+\cdots)$$

然后，单词中立化（Neutralize). 将需要消除性别偏见的单词投影到non-bias direction上去(下图所示)，消除bias维度，例如babysitter，doctor (性别中立的词)等. (另外一些词本质上就和性别有关(grandmother、grandfather、girl、boy、she、he), 就无须理会)

最后，均衡对（Equalize pairs). 让性别对立单词与上面的中立词距离相等，具有同样的相似度. 例如让grandmother和grandfather与babysitter的距离同一化. (下图所示)

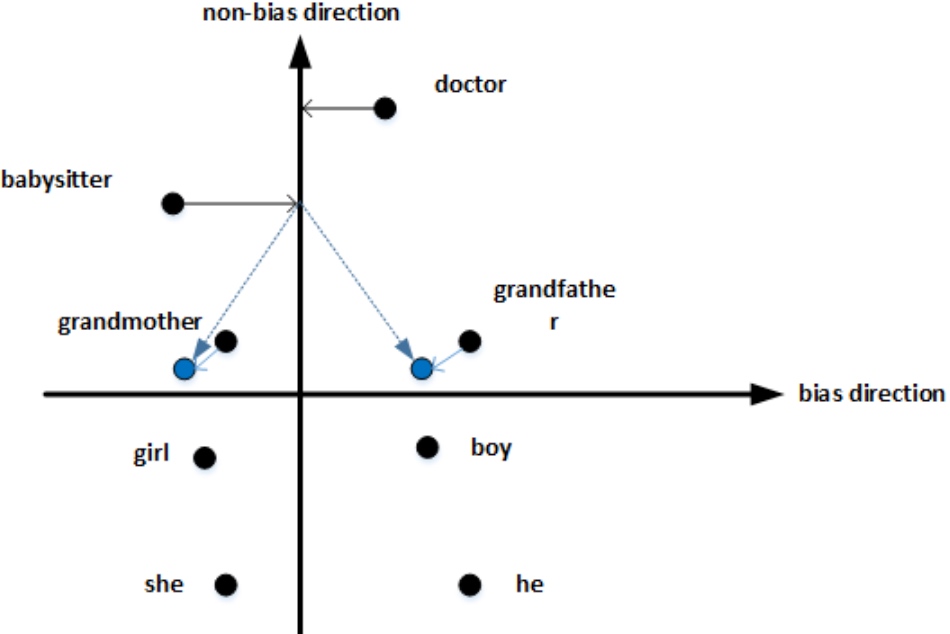
值得注意的是，掌握哪些单词需要中立化非常重要. 一般来说，大部分英文单词，例如职业、身份等都需要中立化，消除embedding vector中性别这一维度的影响

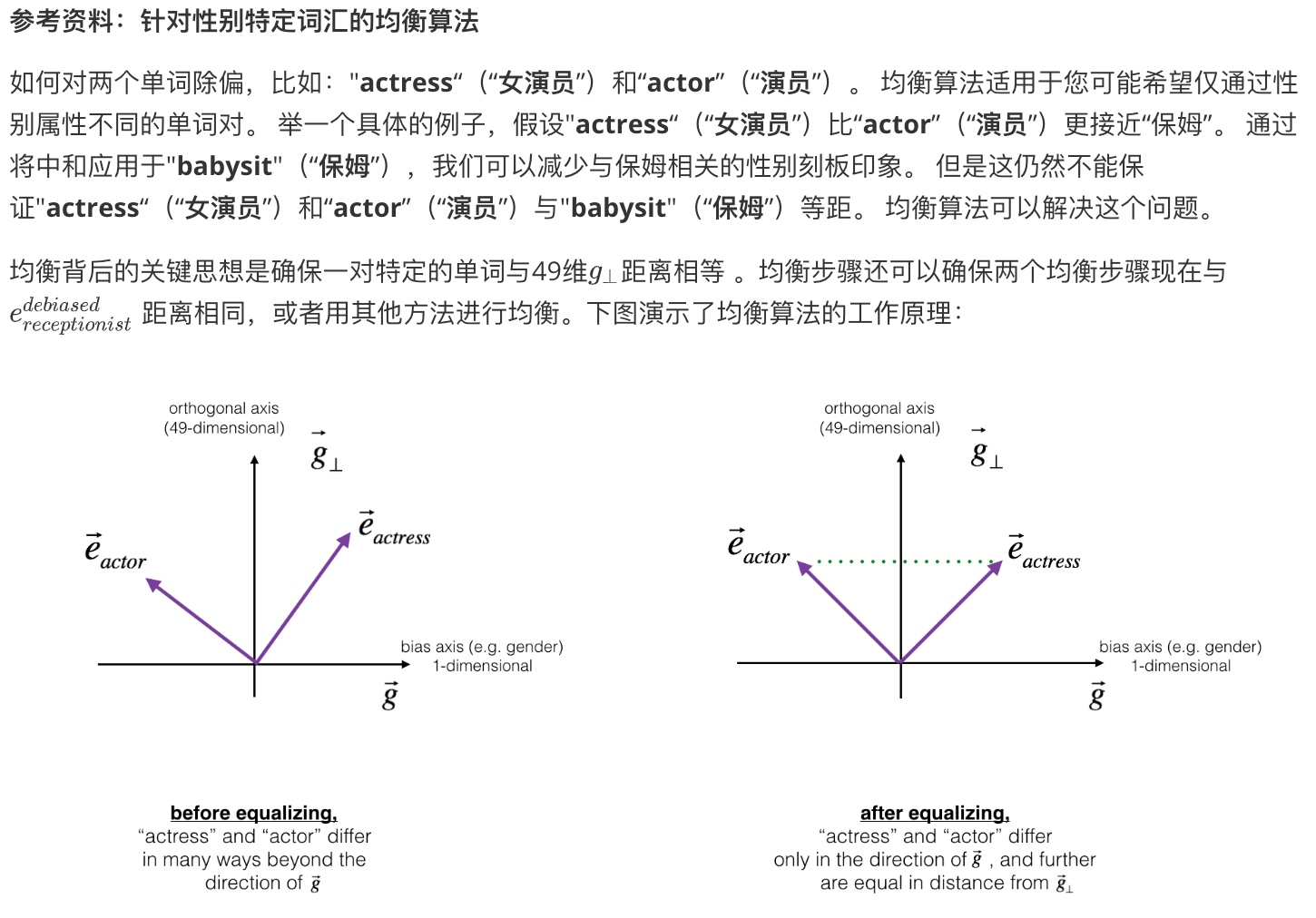
参考论文：Bolukbasi T, Chang K W, Zou J, et al. Man is to Computer Programmer as Woman is to Homemaker? Debiasing Word Embeddings[J]. 2016.

公式的推导主要步骤如下: