为什么选择序列模型？（Why Sequence Models?）

Examples of sequence data

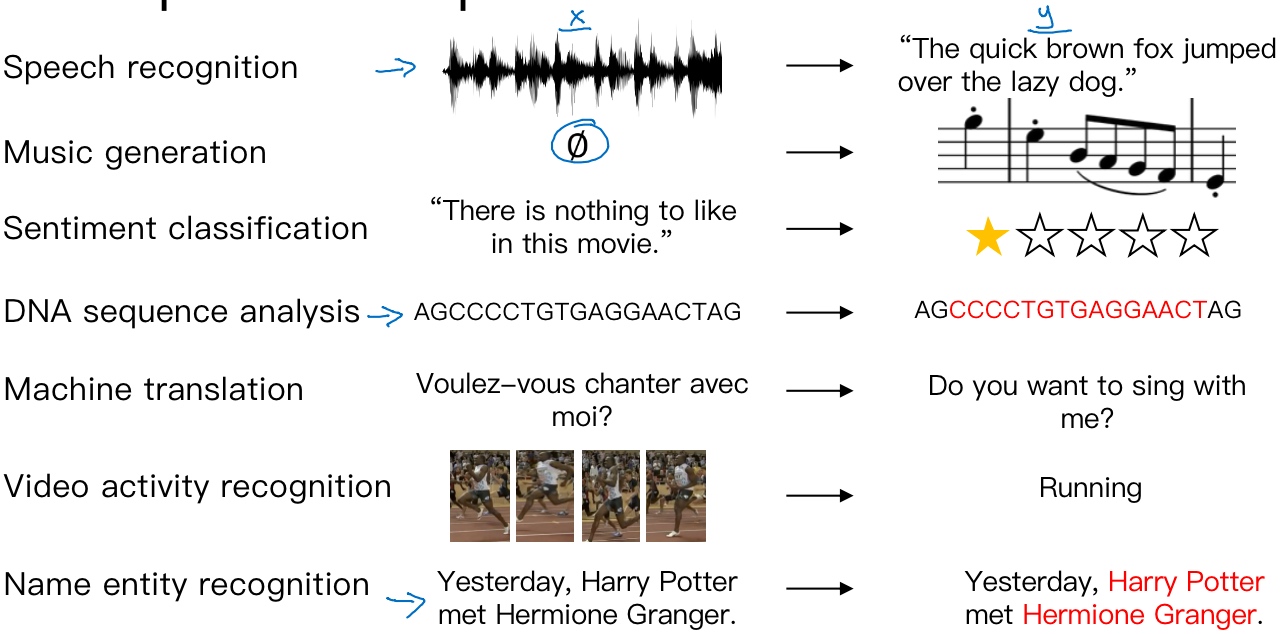
所以这些问题都可以被称作使用标签数据(X,Y)作为训练集的监督学习

但从这一系列例子中可以看出序列问题有很多不同类型

• 输入数据X和输出数据Y都是序列，但X和Y有时也会不一样长
• 输入数据X和输出数据Y都是序列，X和Y有相同的数据长度
• 在另一些问题里，只有X或者Y是序列

数学符号（Notation）

要建立一个能够自动识别句中人名位置的序列模型(命名实体识别问题 Name-Entity Recongition)，它的输入语句是这样的：“Harry Potter and Herminoe Granger invented a new spell.”

输入数据是9个单词组成的序列: $x^{<1>},x^{<2>}, ..., x^{<9>}$ 用$x^{<t>}$来索引这个序列中的位置

t: temporal sequence, used to index the position in the sequence

输出: $y^{<1>},y^{<2>}, ..., y^{<9>}$

$T_x = 9$: length of input sequence

$T_y = 9$: length of output sequence

$x^{(i)<t>}$: 训练样本i的序列中第t个元素

$T_x^{(i)}$: 第i个训练样本的输入序列长度

$y^{(i)<t>}$: 第i个训练样本的输出序列中第t个元素

$T_y^{(i)}$: 第i个训练样本的输出序列的长度

$x^{<t>}$的具体表示:

首先会先制作一个词表/字典:

• 每个词有不同的位置(index)

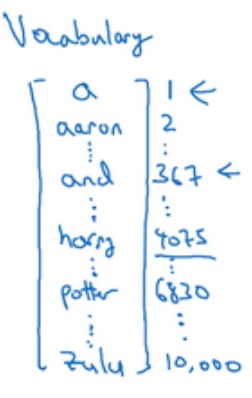
接下来可以用one-hot表示法来表示词典里的每个单词:

• $x^{<1>}$表示Harry这个单词，它就是一个第4075行是1，其余值都是0的向量
• $x^{<t>}$指代句子里的任意词，它就是个one-hot向量，因为它只有一个值是1，其余值都是0，所以会有9个one-hot向量来表示这个句中的9个单词
• 目的是用这样的表示方式表示X，用序列模型在X和目标输出Y之间学习建立一个映射

创建一个新的标记，也就是一个叫做Unknow Word的伪造单词，用作为标记，来表示不在词表中的单词.

循环神经网络模型 (Recurrent Neural Network Model)

Why not a standard network?

Problems:

• Inputs, outputs can be different lengths in different example
• Doesn’t share features learned across different positions of text (具体来说, 如果神经网络已经学习到了在某个$x^{<t>}$, 即’Harry’可能是人名成分，那么如果Harry出现在其他位置，我们希望它也能够自动识别其为人名的一部分, 这是共享特征的结果, 如同CNN网络特点一样. 但是普通的神经网络不具备共享特征的能力)
• $x^{<1>},x^{<2>}, ..., x^{<t>}$每一个都是10000维的one-hot向量, 这是十分庞大的输入层, 因此第一层的权重权重将会有巨量参数. 共享特征还有助于减少神经网络中的参数数量，一定程度上减小了模型的计算复杂度.

Recurrent Neural Network

标准的神经网络不适合解决序列模型问题，而循环神经网络（RNN）是专门用来解决序列模型问题的.

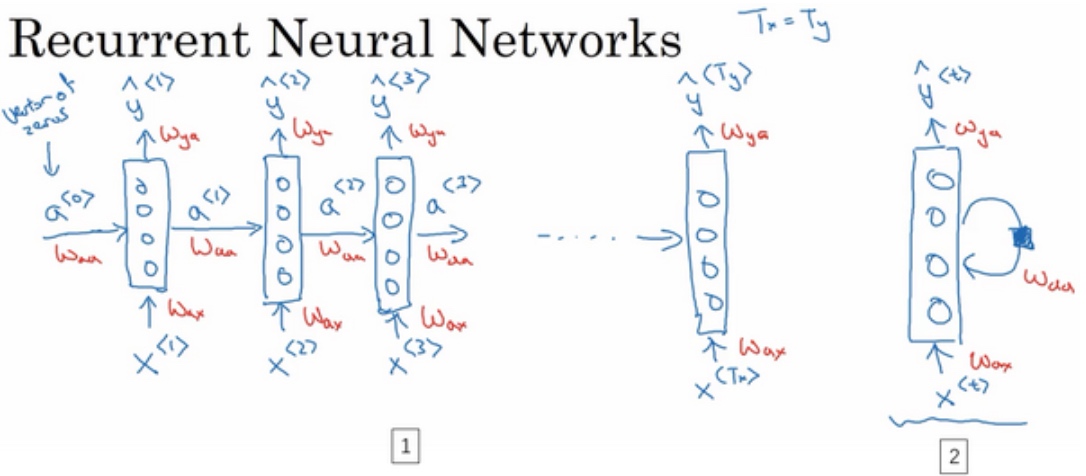
命名实体识别中, 从左到右的顺序读句子, 循环神经网络做的是，当它读到句中的第二个单词$x^{<2>}$时，它不仅用$x^{<2>}$就预测出$\tilde{y}^{<2>}$，他也会输入一些来自时间步1的信息$a^{<1>}$(时间步1的激活值会传递到时间步2), 以此类推. 序列模型从左到右, 依次传递. $x^{<t>}$到$\tilde{y}^{<t>}$之间是隐藏神经元. $a^{<t>}$会被传递到第t+1个元素中, 作为输入. 其中, 在零时刻(t=0)的时候, 需要构造一个激活值$a^{<0>}$, 通常是零向量, 也可以随机初始化.

在一些研究论文/书中会看到上图编号2所示的神经网络，在每一个时间步中，你输入$x^{<t>}$然后输出$y^{<t>}$. 然后画个圈来表示循环连接(表示输回网络层)，画一个黑色方块来表示在这个黑色方块处会延迟一个时间步.

循环神经网络是从左向右扫描数据，同时每个时间步的参数是共享的.(The parameters it uses for each time step are shared)

• 用$W_{ax}$来表示管理着从$x^{<1>}$到隐藏层的连接的一系列参数, 每个时间步使用的都是相同的参数$W_{ax}$
• 而激活值(水平联系)是由参数$W_{aa}$决定的，同时每一个时间步都使用相同的参数$W_{aa}$
• 输出结果由$W_{ya}$决定

注意: $W_{ax}$, 第二个下标x意味着$W_{ax}$要乘以某个x类型的量，然后第一个下标a表示它是用来计算某个a类型的变量

图中的绿色线表示, 在这个循环神经网络中，它的意思是在预测$\tilde{y}^{<3>}$时，不仅要使用$x^{<3>}$的信息，还要使用来自$x^{<1>},x^{<2>}$的信息，因为来自$x^{<1>}$的信息可以通过这样的路径来帮助预测.

但是循环神经网络的一个缺点就是它只使用了这个序列中之前的信息来做出预测 (它在某一时刻的预测仅使用了从序列之前的输入信息并没有使用序列中后部分的信息)

例子:

• He said, ‘Teddy Stephsion was a good man’
• He said, ‘Teddy bears are on sale’
• 如果只给定前三个单词，是不可能确切地知道Teddy是否是人名的一部分，然而第一个例子是人名，第二个例子就不是.

解决方法:

• 双向循环神经网络 - bidirectional RNN（BRNN）

Simplified RNN notataion

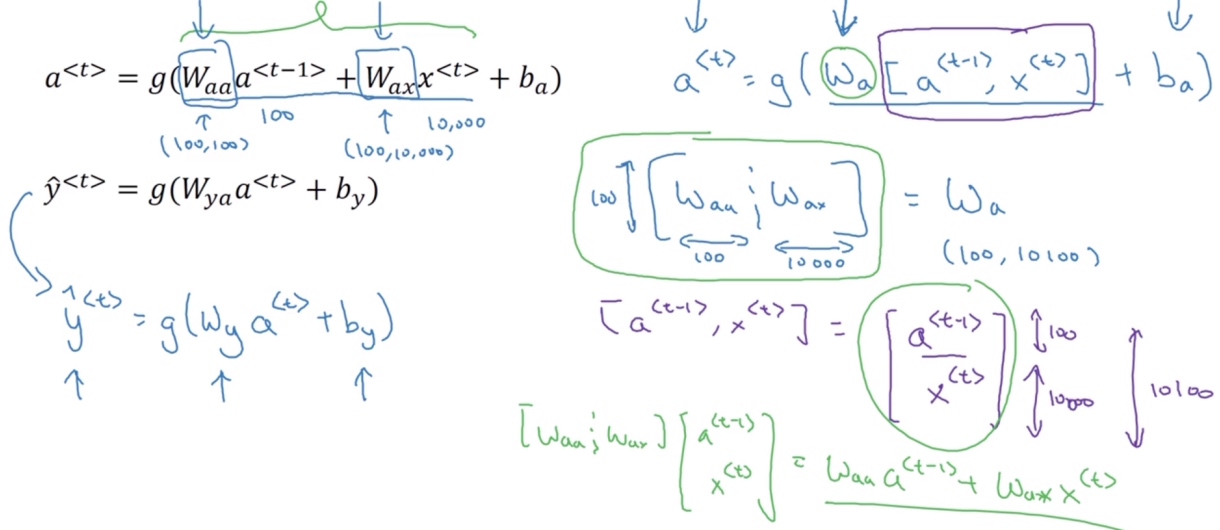
一般开始先输入$a^{<0>}$，它是一个零向量.

接着就是前向传播过程，先计算激活值$a^{<1>}$，然后再计算$y^{<1>}$:

• $a^{<1>} = g_1(W_{aa}a^{<0>} + W_{ax}x^{<1>} + b_a)$
• $\tilde{y}^{<1>} = g_2(W_{ya}a^{<1>}+b_y)$
• 通常$g_1$用的激活函数是tanh / ReLU
• 通常$g_2$用的激活函数是sigmoid / softmax

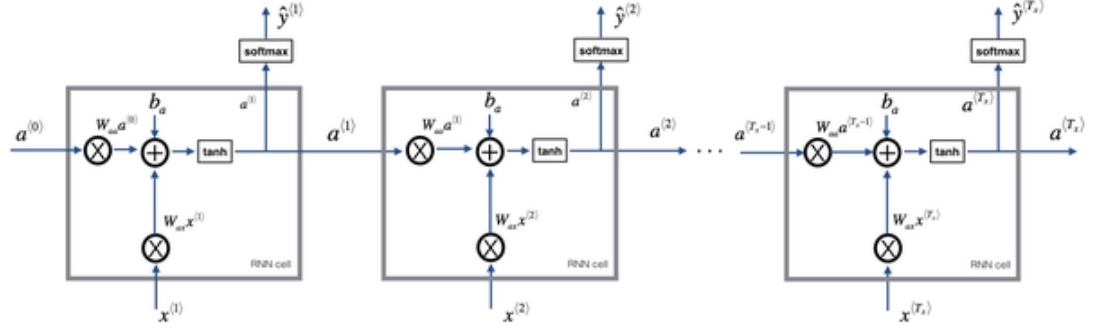
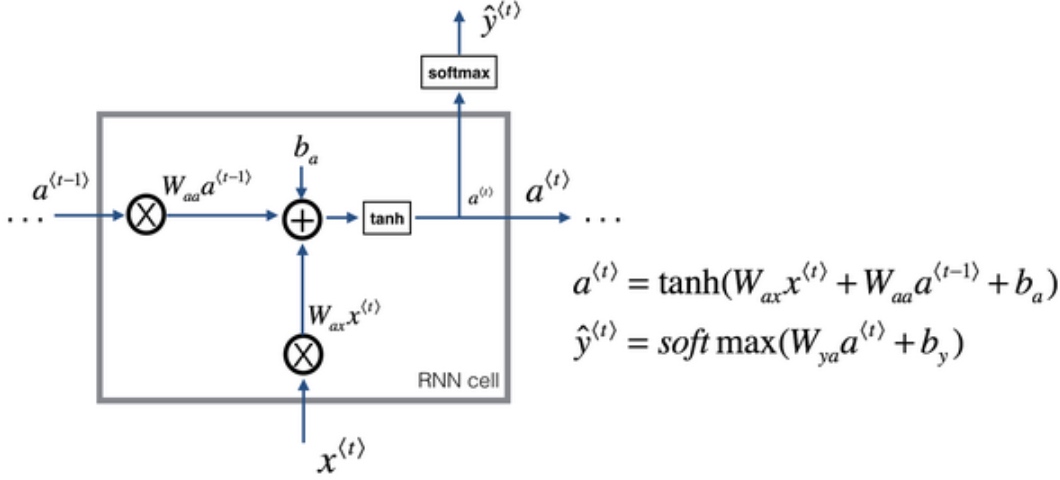
RNN的正向传播（Forward Propagation）过程为:

• $a^{<t>} = g_1(W_{aa}a^{<t-1>} + W_{ax}x^{<t>} + b_a)$
• $\tilde{y}^{<t>} = g_2(W_{ya}a^{<t>}+b_y)$

简化后就变成:

• $a^{<t>} = g_1(W_{a}[a^{<t-1>},x^{<t>}] + b_a)$
• $\tilde{y}^{<t>} = g_2(W_{y}a^{<t>}+b_y)$

定义$W_{a}$的方式是将矩阵$W_{aa}$和矩阵$W_{ax}$水平并列放置 ==> $[W_{aa}:W_{ax}] = W_{a}$.

• 如果a是100维的, x是10000维的, 那么$W_{aa}$就是个(100, 100)维的矩阵, $W_{ax}$就是个(100, 10000)维的矩阵. 将两个矩阵堆起来, $W_a$就会是个(100, 10100)维的矩阵.

而$[a^{<t-1>},x^{<t>}]$就是将两个向量堆在一起, 即$\begin{bmatrix} a^{<t-1>} \\ x^{<t>}\end{bmatrix}$, 最终这就是个10100维的向量

矩阵$[W_{aa}:W_{ax}]$乘以$\begin{bmatrix} a^{<t-1>} \\ x^{<t>}\end{bmatrix}$，刚好等于$W_{aa}a^{<t-1>} + W_{ax}x^{<t>}$

RNN前向传播示意图：

例子

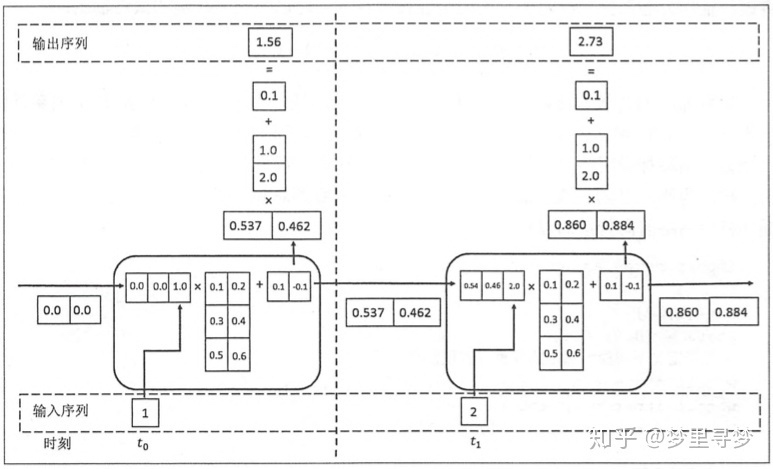
如上图所示，假设节点状态的维度为2，节点的输入和输出维度为1，那么在循环体的全连接层神经网络的输入维度为3，也就是将上一时刻的状态与当前时刻的输入拼接成一维向量作为循环体的全连接层神经网络的输入，在这里t0时刻的节点状态初始化为[0.0, 0.0]，t0时刻的节点输入为[1.0]，拼接之后循环体的全连接层神经网络的输入为[0.0, 0.0, 1.0]，循环体中的全连接层的权重表示为二维矩阵[[0.1, 0.2], [0.3, 0.4], [0.5, 0.6]]，偏置项为[0.1, -0.1]，我们可以看到权重矩阵和偏置项在t0和t1时刻的循环体中是一样的，这也说明了RNN结构中的参数在不同时刻中也是共享的。经过循环体中的全连接层神经网络后节点的状态改变为tanh([0.6, 0.5]) = [0.537, 0.462]，当前节点状态的输出作为下一个节点状态的输入.

为了将当前时刻的状态转变为节点的最终输出，RNN中还有另外一个全连接神经网络来计算节点输出，在图2中被表示为[0.537, 0.462] * [1.0, 2.0] + [0.1] = [1.56]，用于输出的全连接层权重为[1.0, 2.0]，偏置项为[0.1]，1.56表示为t0时刻节点的最终输出.

得到RNN的前向传播结果之后，和其他神经网络类似，定义损失函数，使用反向传播算法和梯度下降算法训练模型，但RNN唯一的区别在于：由于它每个时刻的节点都有一个输出，所以RNN的总损失为所有时刻（或部分时刻）上的损失和.

通过时间的反向传播（Backpropagation through time）

Forward propagation and backpropagation

反向传播(红色箭头所指方向)地计算方向与前向传播(蓝色箭头所指方向)基本上是相反的.

然后为了计算反向传播，还需要一个损失函数(交叉熵损失函数（Cross Entropy Loss))$L^{<t>}(\tilde{y}^{<t>},{y}^{(t)})=-y^{(t)}log\tilde{y}^{(t)}-(1-{y}^{(t)})log(1-\tilde{y}^{(t)})$

它对应的是序列中一个具体的词，如果它是某个人的名字，那么$y^{(t)}$的值就是1，然后神经网络将输出这个词是名字的概率值，比如0.1.

整个序列的损失函数，将定义为$L(\tilde{y},{y}) = \sum_{t=1}^{T_x}L^{<t>}(\tilde{y}^{<t>},{y}^{(t)})$

具体来看, 在这个计算图中，通过$\tilde{y}^{<1>}$可以计算对应时间步的损失函数，（上图编号3所示), 以此类推直到最后一个时间步，最后把每个单独时间步的损失函数都加起来, 计算出总体损失函数.

最终要做的就是把前向传播的箭头都反过来，在这之后就可以通过导数计算相关的参数，用梯度下降法来更新参数($W_y,b_y,W_a,b_a$).

RNN反向传播示意图:

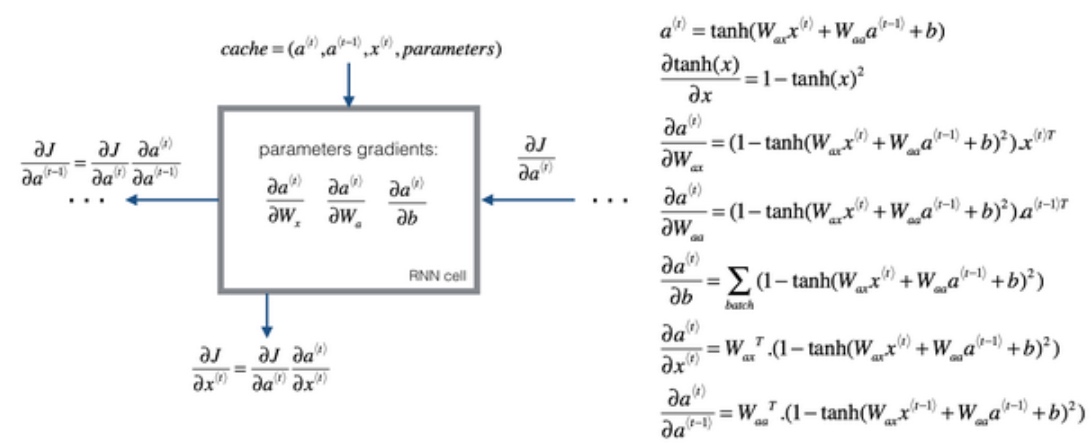
不同类型的循环神经网络（Different types of RNNs）

内容参考了Andrej Karpathy的博客，一篇叫做《循环神经网络的非理性效果》（“The Unreasonable Effectiveness of Recurrent Neural Networks”）的文章

Summary of RNN types

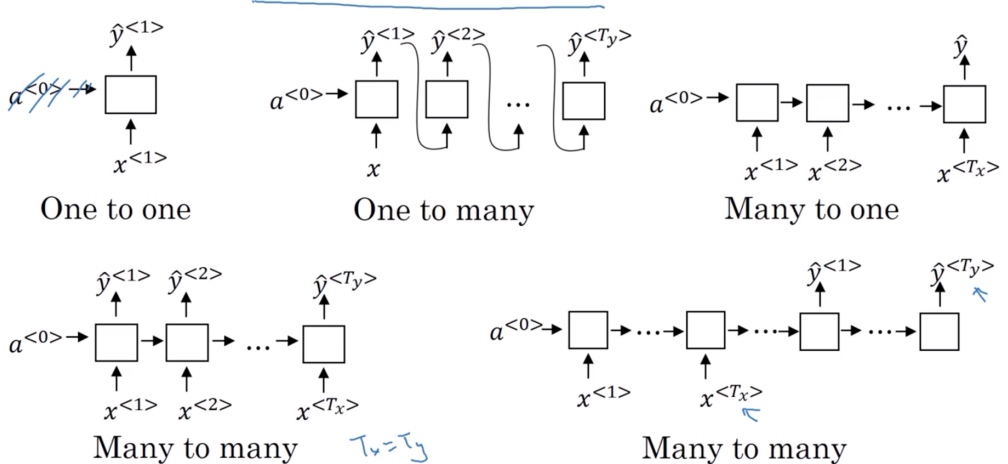
One to One:

• When remove $a^{[0]}$, it is a standard neural network

One to Many: - Music generation / sequence generation - $T_x$ may be 1 or $\emptyset$, E.g. input one genre of music that you would like to generate - When you are generating sequences, often you feed the first synthesized output to the next layer

Many to One:

• Sentiment analysis
• Input comments, output a rating number

Many to Many ($T_x = T_y$):

• Name entity recognition

Many to Many ($T_x != T_y$):

• Machine translation
• encoder-decoder architecture
• attention model

语言模型和序列生成（Language model and sequence generation）

对于语音识别系统来说, 下面两个句子是极其相似的:

‘The apple and pair salad’

‘The apple and pear salad’

而让语音识别系统去选择第二个句子(make more sense)的方法就是使用一个语言模型，他能计算出这两句话各自的可能性.

language model: Given any sentence, it tells you what is the probability of that particular sentence (estimates the probability of that particular sequence of words)

语言模型所做的就是，它会告诉你某个特定的句子它出现的概率是多少. 输入一个句子，准确地说是一个文本序列$y^{<1>},y^{<2>},...,y^{<T_y>}$

为了使用RNN建立一个语言模型, 需要一个训练集, 包含一个很大的英文文本语料库（corpus）或者其它的语言. 语料库是自然语言处理的一个专有名词，意思就是数量众多的英文句子组成的文本

一. 标识化

假如在训练集中得到这么一句话,

‘Cats average 15 hours of sleep a day.’

要做的第一件事就是将这个句子标记化(建立一个字典，然后将每个单词都转换成对应的one-hot向量(字典中的索引))

定义句子的结尾, 增加一个额外的标记, 叫作<EOS>, 它表示句子的结尾.

因此, 不包括句号会有9个输入$y^{<1>},y^{<2>},...,y^{<9>}$

有另一句话,

‘The Egyptian Mau is a bread of cat.’

其中有一个词Mau, 并不在预先的那10000个最常用的单词中. 因此,可以把Mau替换成一个叫做<UNK>的代表未知词的标志. 然后只针对UNK建立概率模型, 而不是针对这个具体的词Mau.

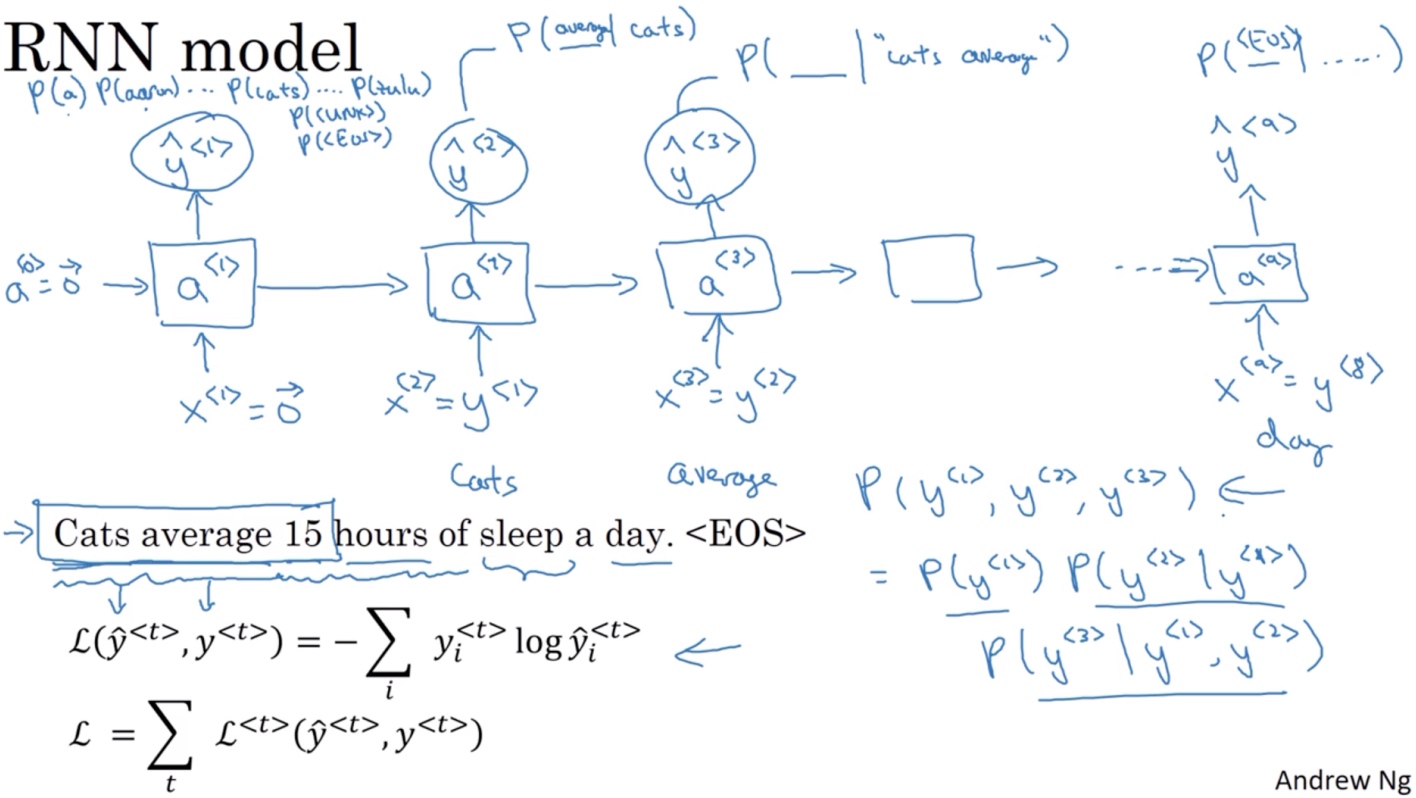
二. RNN建立序列的概率模型

• 在第0个时间步
  • 计算激活项$a^{<1>}$，它是以$x^{<1>}$作为输入的函数, 而会被设为全为0的集合(0向量)
  • 然后通过一个softmax层来预测字典中的任意单词会是第一个词的概率, $\tilde{y}^{<1>}$
  • softmax层输出10,002种结果(每个词的概率), 因为字典中有10,002个词 $P(a), P(cats),P(<UNK>), ...,P(<EOS>)$
• 在第1个时间步
  • 仍然使用激活项$a^{<1>}$
  • 由于第一个词是’cats’的概率最大, 所以$x^{<2>} = y^{<1>}$
  • 同样softmax层输出10,002种结果, $P(average|cats), ..., P(<EOS>|cats)$
• … 以此类推
• 所以$x^{<t>} = y^{<t-1>}$

三. 代价函数

• 在某个时间步t, 如果真正的词是$y^{<t>}$，而神经网络的softmax层预测结果值也是$y^{<t>}$，
• 那么softmax损失函数就是$L(\tilde{y}^{<t>},y^{<t>}) = -\sum_iy_i^{<t>}log\tilde{y}_i^{<t>}$
• 而总体损失函数就是$L= \sum_tL^{<t>}(\tilde{y}^{<t>},y^{<t>})$ (把所有单个预测的损失函数都相加起来)

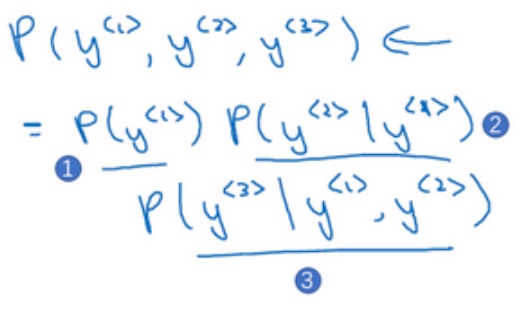
有一个新句子，它是$y^{<1>},y^{<2>},y^{<3>}$, 现在要计算出整个句子中各个单词的概率，方法就是:

• 第一个softmax层会告诉你$y^{<1>}$的概率, 这也是第一个输出
• 然后第二个softmax层会告诉你在考虑$y^{<1>}$的情况下$y^{<2>}$的概率
• 然后第三个softmax层告诉你在考虑$y^{<1>},y^{<2>}$的情况下$y^{<3>}$的概率
• 把这三个概率相乘，最后得到含3个词的整个句子的概率

对新序列采样（Sampling novel sequences）

在训练一个序列模型之后，要想了解到这个模型学到了什么，一种非正式的方法就是进行一次新序列采样.

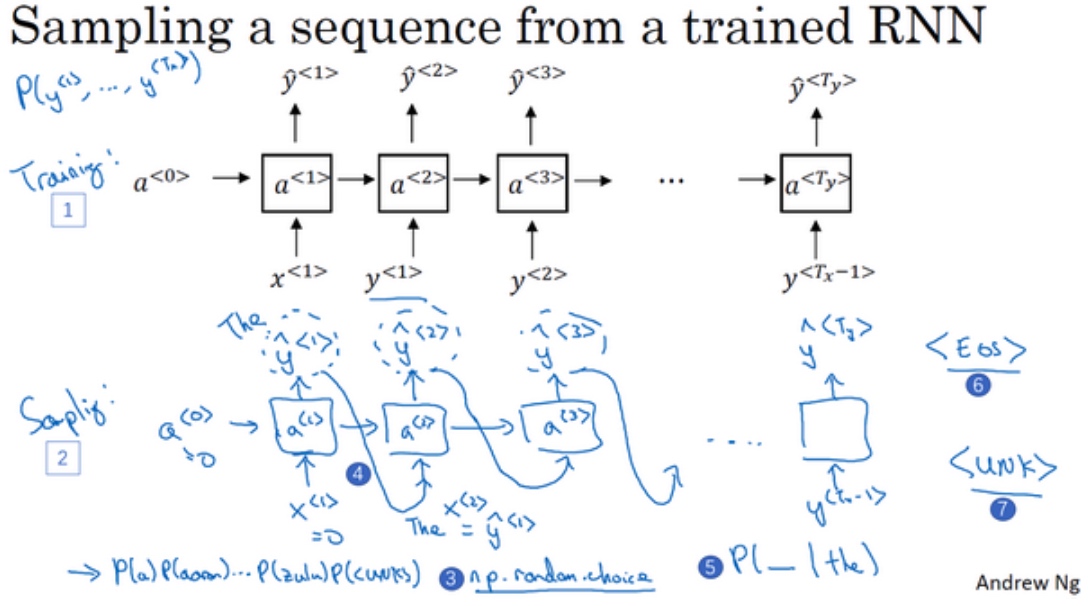
一个序列模型(编号1所示的网络)模拟了任意特定单词序列的概率, 要做的就是对这些概率分布进行采样来生成一个新的单词序列(编号2所示的网络).

1. 对模型生成的第一个词进行采样
   • 输入$x^{<1>} = 0,a^{<0>} = 0 $
   • 对这个向量使用np.random.choice, 来根据向量中这些概率的分布进行采样, 这样就能对第一个词进行采样了
2. 继续下一个时间步,
   • 需要$\tilde{y}^{<1>}$作为输入
   • 然后softmax层就会预测$\tilde{y}^{<2>}$是什么
   • 然后再次用这个采样函数来对$\tilde{y}^{<2>}$进行采样
3. 无论得到什么样的用选择结果(one-hot码表示的)，都把它传递到下一个时间步，然后对第下一个词进行采样，一直这样直到最后一个时间步
4. 这就是你如何从你的RNN语言模型中生成一个随机选择的句子

def choice(a, size=None, replace=True, p=None) - 表示从a中随机选取size个数 - replacement 代表的意思是抽样之后还放不放回去，如果是False的话，那么通一次挑选出来的数都不一样，如果是True的话， 有可能会出现重复的，因为前面的抽的放回去了。 - p表示每个元素被抽取的概率，如果没有指定，a中所有元素被选取的概率是相等的。

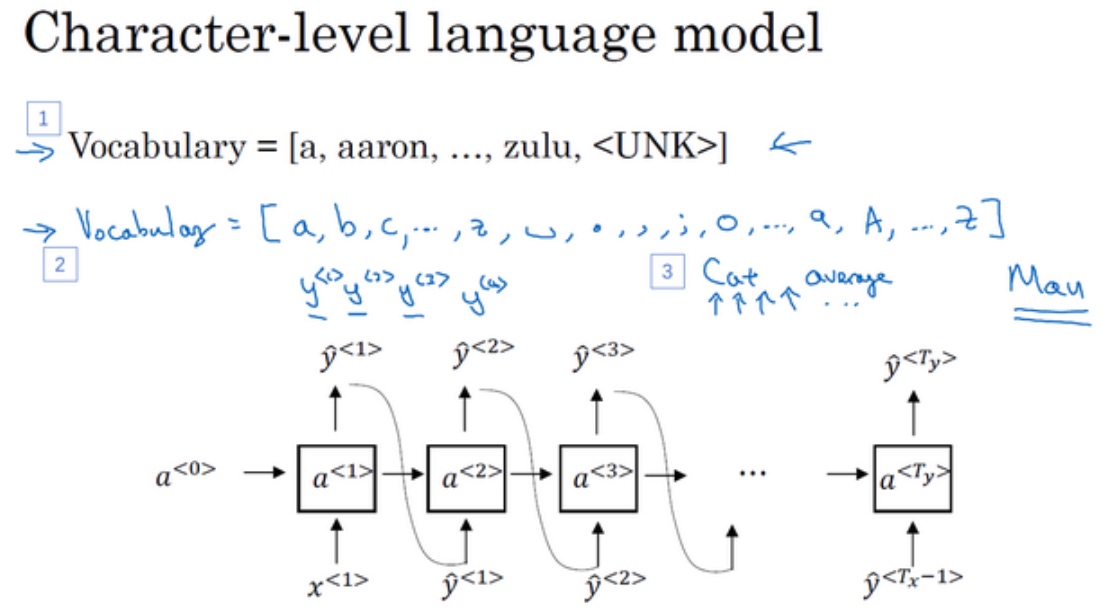
也以构建一个基于字符的RNN结构, 字典包含从a到z的字母… “Cats average 15 hours of sleep a day.”, 在该例中C就是$\tilde{y}^{<1>}$，a就是$\tilde{y}^{<2>}$，t就是$\tilde{y}^{<3>}$，空格符就是$\tilde{y}^{<4>}$等等

基于字符的语言模型

缺点: 最后会得到太多太长的序列

优点: 不必担心会出现未知的标识, 对于基于词汇的语言模型，如果Mau不在字典中，只能把它当作未知标识UNK; 但是在基于字符的语言模型, 它会被拆成’M’,‘a’,‘u’, 为一个可能性非零的序列.

Sequence Generation

循环神经网络的梯度消失（Vanishing gradients with RNNs）

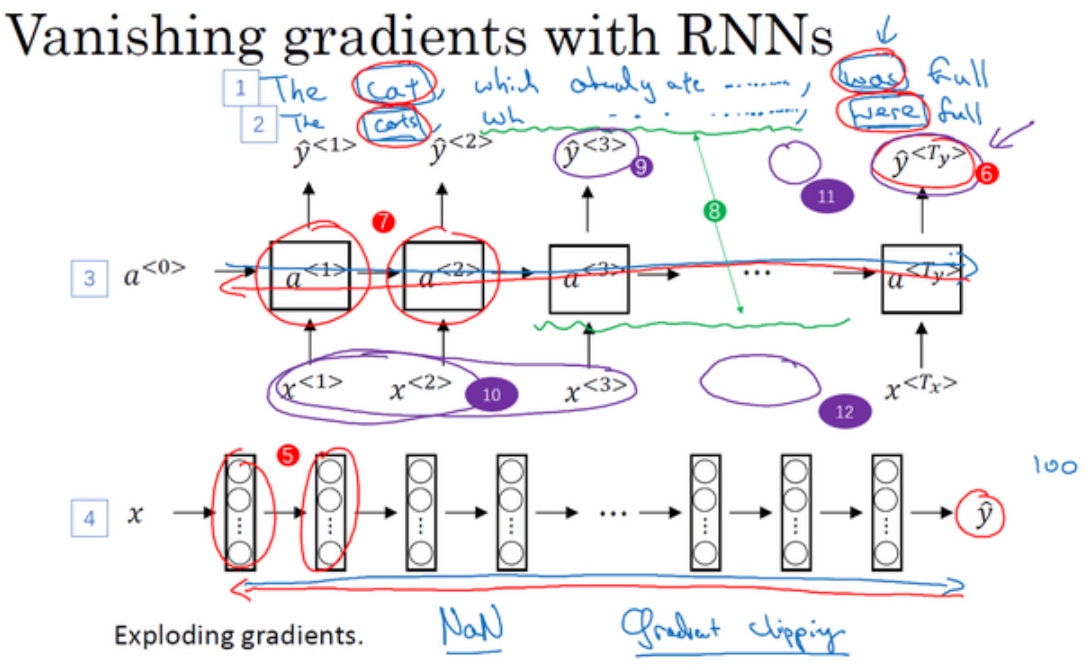
‘The cat, which already ate ……, was full.’

‘The cats, which ate ……, were full.’

例子中的句子有长期的依赖(were/was依赖前面的cats/cat). 但是基本的RNN模型, 不擅长捕获这种长期依赖效应.

训练很深的神经网络时，随着层数的增加，导数有可能指数型的下降或者指数型的增加(梯度消失或者梯度爆炸的问题). 从输出$\tilde{y}$得到的梯度很难传播回去，很难影响靠前层的权重，很难影响前面层的计算.

同样, 一个RNN处理1,000 or 10,000个时间序列的数据集, 这就是一个1,000 or 10,000层的神经网络，这样的网络就会遇到上述类型的问题. 这就意味着，实际上很难让一个神经网络能够意识到它要记住看到的是单数名词还是复数名词，然后在序列后面生成依赖单复数形式的was或者were. 用基本的RNN, 例如图中输出$\tilde{y}^{<3>}$(编号9所示), 只受附近的输入值(编号10所示)的影响.

梯度爆炸(梯度指数型上升), 会使参数变得极其大，以至于网络参数崩溃, 会看到很多NaN(Not a Number), 意味着网络计算出现了数值溢出.

解决方法就是用梯度修剪: 观察梯度向量, 如果它大于某个阈值, 缩放梯度向量, 保证它不会太大

梯度消散(Gradient Vanishing) It is difficult for the output to be strongly influenced by an input that was very early in the sequence, it is just very difficult for the area to back propagate all the way to the beginning of the sequence. Therefore, to modify how the neural network is doing computations earlier in the sequence. If we dun address it, it wont be very good at capturing long-range dependencies.

Gated recurrent unit which is a very effective solution for addressing the vanishing gradient problem and will allow your network to capture much longer range dependencies. It is a modification to the RNN hidden layer that makes it much better capturing long range connection.

GRU单元 (Gated Recurrent Unit)

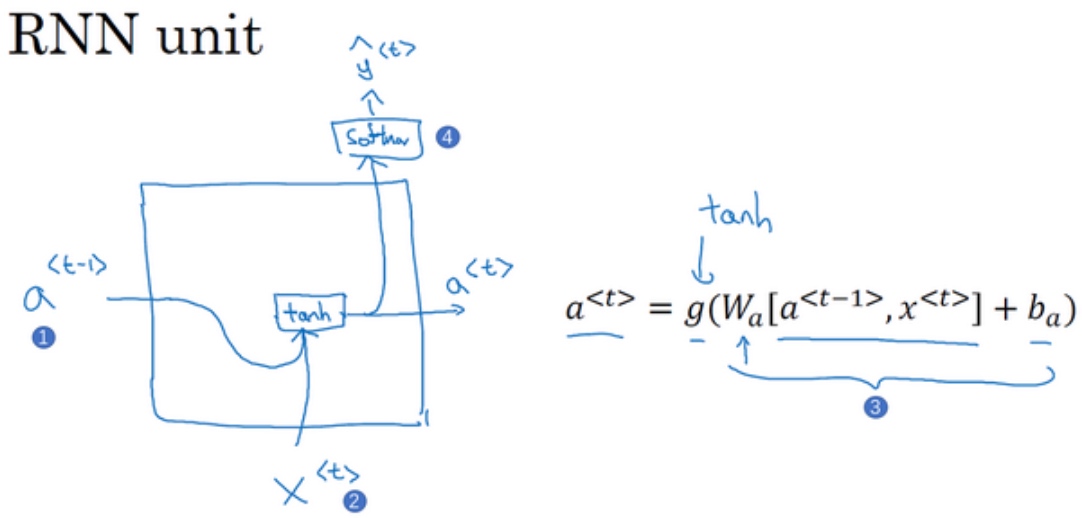
$a^{<t>} = g(W_{a}[a^{<t-1>},x^{<t>}] + b_a)$在RNN的时间t处，计算激活值. 具体来看, 输入$a^{<t-1>}$(上一个时间步的激活值), 再输入$x^{[t]}$, 把这两个并起来后乘上权重项, 在这个线性计算之后, 经过tanh计算得到激活值$a^{<t>}$. 激活值将会传softmax单元(或者其他用于产生输出的东西).

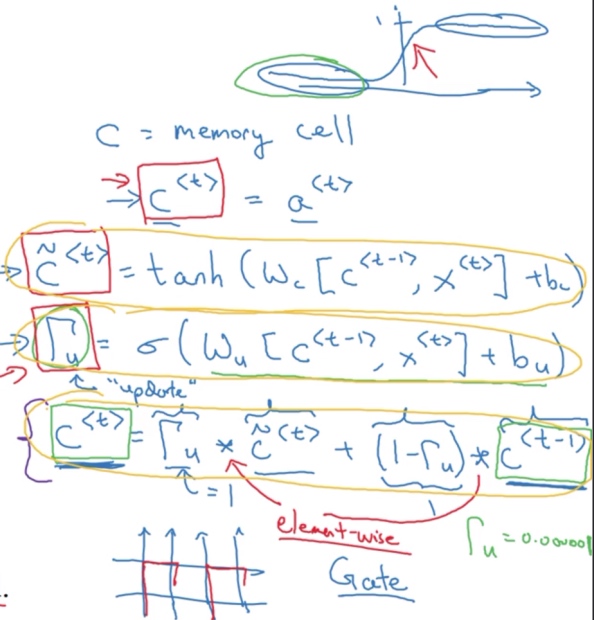
1. GRU单元将会有个新的变量称为c (memory cell). 记忆细胞的作用是提供了记忆的能力, 比如说一只猫是单数还是复数, 所以当它看到之后的句子的时候, 它仍能够判断句子的主语是单数还是复数. 对于简单版本的GRU, 实际上它输出了激活值$a^{<t>}$, $c^{<t>} = a^{<t>}$
2. 在每个时间步, 考虑一个候选值$\tilde{c}^{<t>}$去重写记忆细胞(代替$c^{<t>}$的值). 用tanh激活函数来计算$\tilde{c}^{<t>} = tanh(W_c[c^{<t-1>}, x^{<t>}]+b_c)$
3. GRU中真正重要的思想是有一个门, $\Gamma_u = \sigma(W_u[c^{<t-1>}, x^{<t>}]+b_u)$
   • u代表更新门, 值在0 - 1之间(因为用了sigmoid函数), 对于大多数可能的输入, sigmoid函数的输出总是非常接近0或者非常接近1.
   • 门决定是否要真的要用$\tilde{c}^{<t>}$更新$c^{<t>}$
4. 接下来要给GRU用的式子, $c^{<t>} = \Gamma_u * \tilde{c}^{<t>} + (1 - \Gamma_u)*c^{<t-1>}$
   • ‘*’ is element-wise multiply
   • 当$\Gamma_u = 1$时, $c^{<t>} = \tilde{c}^{<t>}$

具体来看,

“The cat, which already ate……, was full.”

“The cats, which already ate……, were full.”

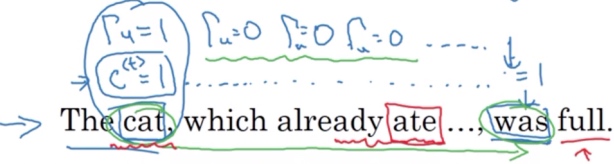
1. 在’cat’位置的时候, 记忆细胞$c^{<t>}$将被设定为0或者1 (单数为1,复数为0), GRU单元将会一直记住$c^{<t>}$的值; 同时, 将门值$\Gamma_u$设为1
2. 然后往前再更新这个值$\Gamma_u$, 对于所有在这中间的值, 门的值应该设为0 ($\Gamma_u=0$), 意思就是说不更新它，就用旧的值 (因为$\Gamma_u=0$, 则$c^{<t>}=c^{<t-1>}$, $c^{<t>}$等于旧的值).
   • 直到’was’的位置, $c^{<t>}$的值还是1 ($c^{<t>}$的值还是等于$c^{<t-1>}$), 于是它仍然记得猫是单数的, 所有用了’was’.
   • $\Gamma_u$的作用就是决定什么时候会更新$c^{<t>}$值,
3. 到句子遍历完, 就可以忘记$c^{<t>}$值了

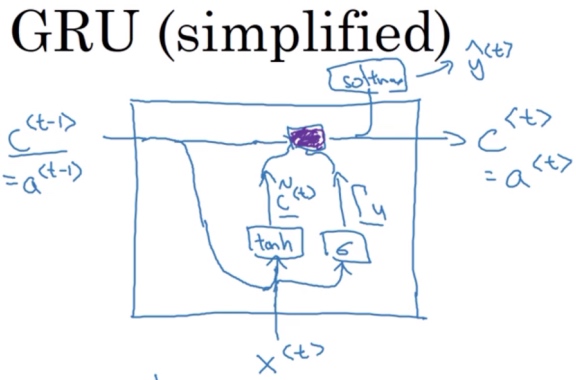
GRU的图像表示

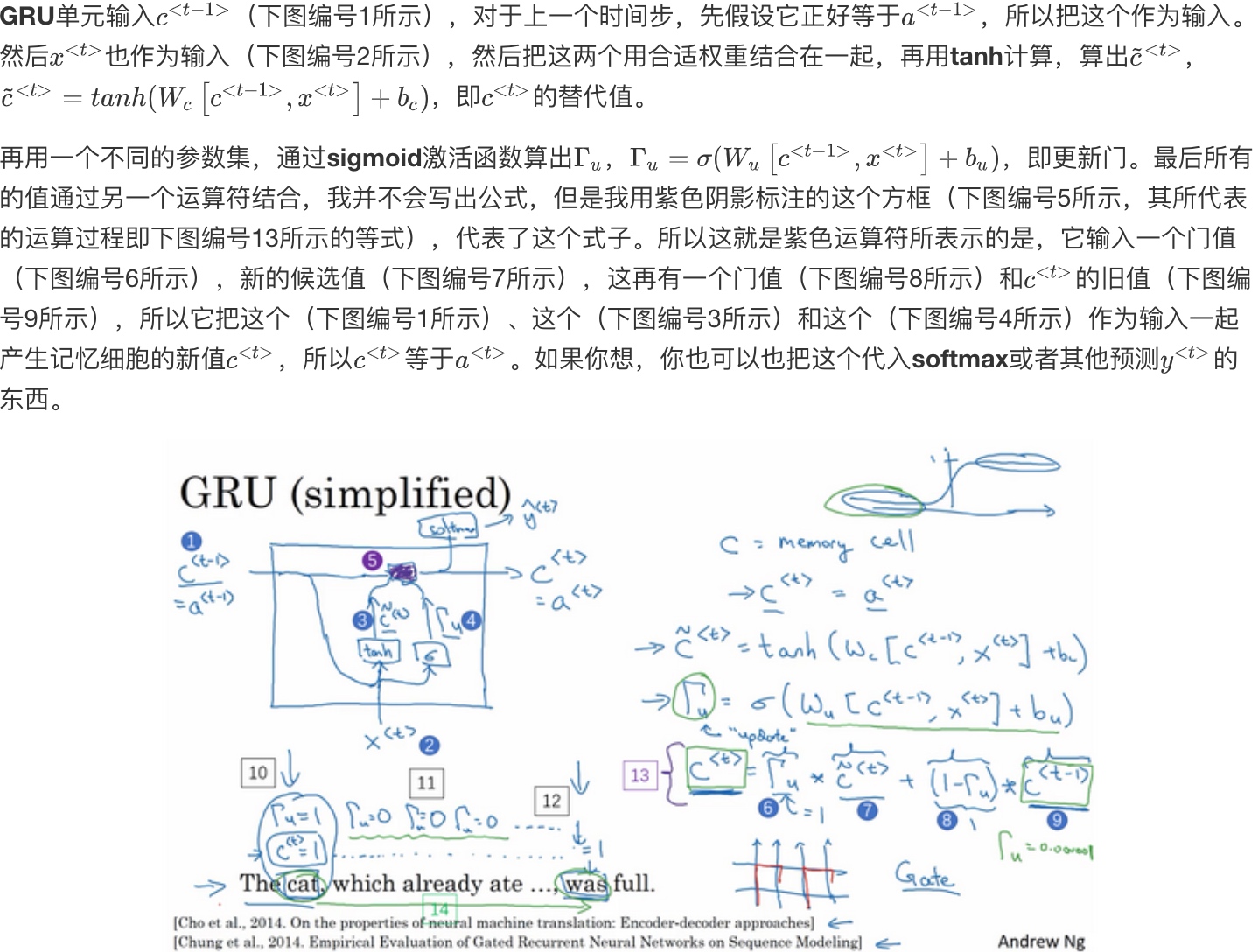
GRU单元的优点就是通过门决定是否某个记忆细胞.

因为sigmoid函数的关系, 门很容易取到0值(只要这个值是一个很大的负数)或者说非常接近0. 所以在这样的情况下, 更新式子$c^{<t>} = \Gamma_u * \tilde{c}^{<t>} + (1 - \Gamma_u)*c^{<t-1>}$就会变成$c^{<t>}=c^{<t-1>}$, 这非常有利于维持记忆细胞的值. 同时因为$\Gamma_u$很接近0, 这就不会有梯度消失的问题了, 即使经过很多很多的时间步. 因此这允许神经网络运行在非常庞大的依赖词上，比如说cat和was单词即使被中间的很多单词分割开.

细节:

• $c^{<t>}$可以是一个向量.
  • 假设有100维的隐藏的激活值, 那么$c^{<t>}, \tilde{c}^{<t>}, \Gamma_u$, 也是100维, 他们具有相同维度
  • $\Gamma_u$是100维的向量，里面的值几乎都是0或者1, 它告诉了100维的记忆细胞$c^{<t>}$哪些是要更新的bit.
  • 比如说你可能需要一个比特来记忆猫是单数还是复数，其他比特来理解你正在谈论食物，然后你稍后可能就会谈论“The cat was full.”，你可以每个时间点只改变一些bit

Full GRU

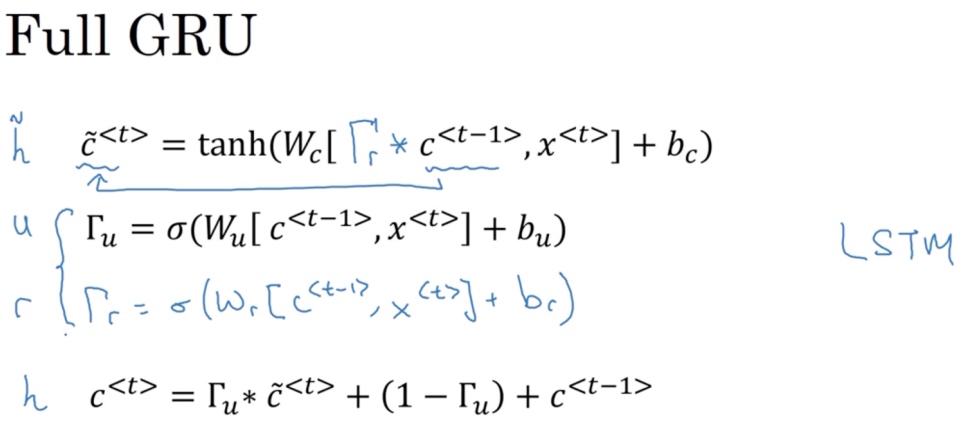
计算的第一个式子中给记忆细胞的新候选值加上一个新的门$\Gamma_r$, r代表相关性（relevance）. 这个门告诉你计算出的下一个$c^{<t>}$的候选值$\tilde{c}^{<t>}$跟$c^{<t-1>}$有多大的相关性

计算这个门$\Gamma_r$需要参数, 因此多了一个新的参数矩阵 $\Gamma_r = \sigma(W_r[c^{<t-1>}, x^{<t>}]+b_r)$

在有些文章中, 会用到$\tilde{x},u,r,h$符号来表示这些量

LSTM单元（long short term memory unit)

[Hochreiter S, Schmidhuber J. Long Short-Term Memory[J]. Neural Computation, 1997, 9(8):1735-1780.]

LSTM即长短时记忆网络, 比GRU更加有效.

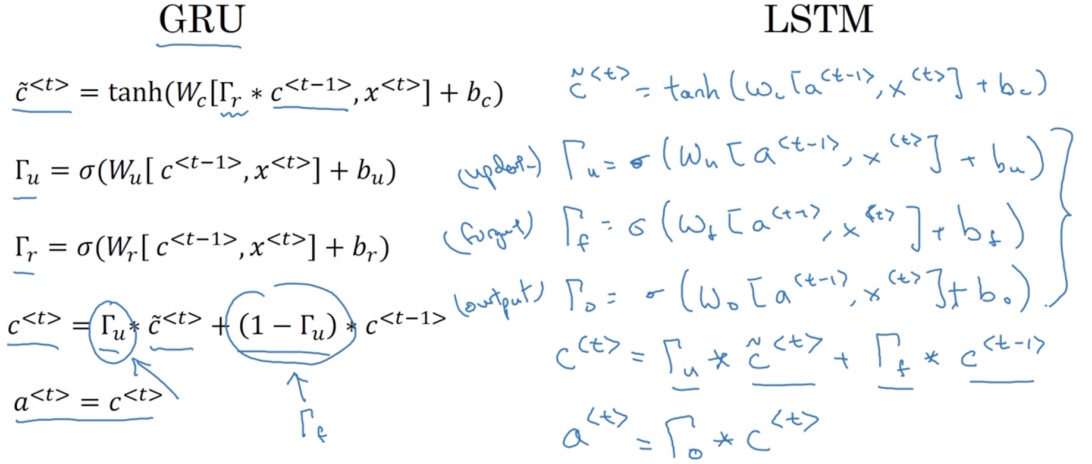
LSTM的公式与GRU的不同:

• 候选值$\tilde{c}^{[t]}$公式中, 使用$a^{[t-1]}$代替$c^{[t-1]}$, 因此在LSTM中不再有的情况$a^{[t]}= c^{[t]}$
• 不再使用相关门$\Gamma_r$
• 多了遗忘门$\Gamma_f$(the forget gate) 和 输出门$\Gamma_o$(output gate)
• 记忆细胞的更新值 $c^{[t]} = \Gamma_u * \tilde{c}^{[t]} + \Gamma_f * c^{[t-1]}$, 给了记忆细胞选择权去维持旧的值$c^{[t-1]}$或者就加上新的值$\tilde{c}^{[t]}$
• 最后$a^{[t]} = \Gamma_o * c^{[t]}$

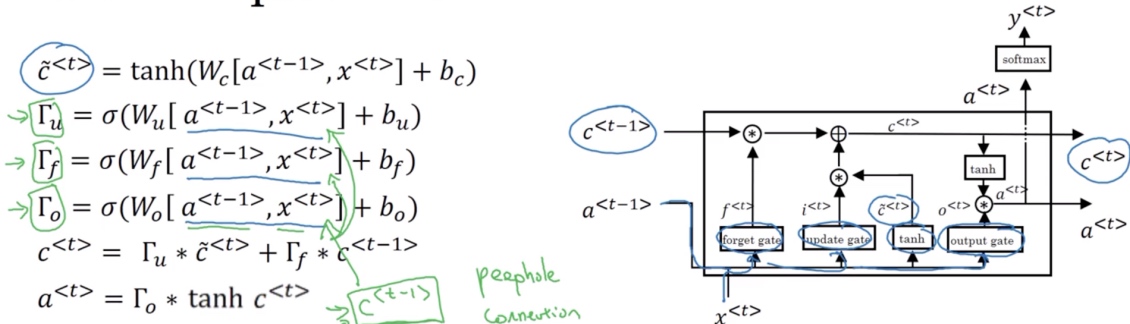
张图里是用$a^{[t-1]}, x^{[t]}$一起来计算遗忘门$\Gamma_f$的值, 还有更新门$\Gamma_u$以及输出门$\Gamma_o$. 然后它们也经过tanh函数来计算$\tilde{c}^{[t]}$, 这些值被用复杂的方式(元素对应的乘积或其他)组合在一起, 来从之前的$c^{[t-1]}$中获得$c^{[t]}$

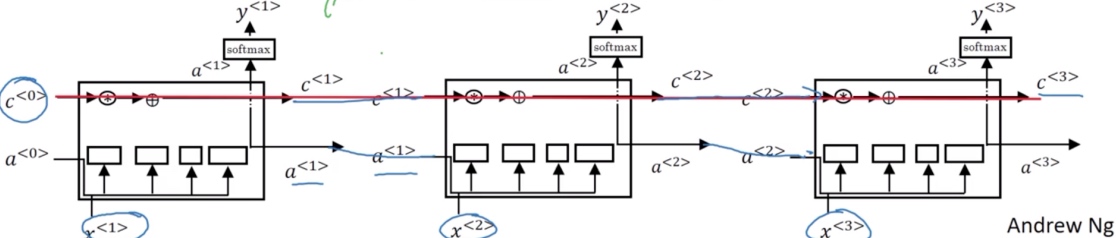
注意图中红色箭头, 这条线显示了只要正确地设置了遗忘门和更新门, LSTM是相当容易把的值$c^{[0]}$一直往下传递到右边, 比如$c^{[0]}=c^{[3]}$. 这就是为什么LSTM和GRU非常擅长于长时间记忆某个值，对于存在记忆细胞中的某个值，即使经过很长很长的时间步

LSTM另外一些版本可能门值不仅取决于$a^{<t-1>}, x^{<t>}$, 有时候也可以偷窥(取决)一下上一个记忆细胞的值$c^{<t-1>}$, 这叫做”窥视孔连接”(peephole connection). 后“偷窥孔连接”就可以结合这三个门（$\Gamma_u,\Gamma_f,\Gamma_o$）来计算了. 第n个$c^{<t-1>}$的元素只会影响第n个元素对应的那个门.

LSTM前向传播图:

LSTM反向传播计算:

GRU的优点是这是个更加简单的模型，所以更容易创建一个更大的网络，而且它只有两个门，在计算性上也运行得更快，然后它可以扩大模型的规模

LSTM更加强大和灵活，因为它有三个门而不是两个

双向循环神经网络（Bidirectional RNN）

双向RNN模型可以让你在序列的某点处不仅可以获取之前的信息，还可以获取未来的信息 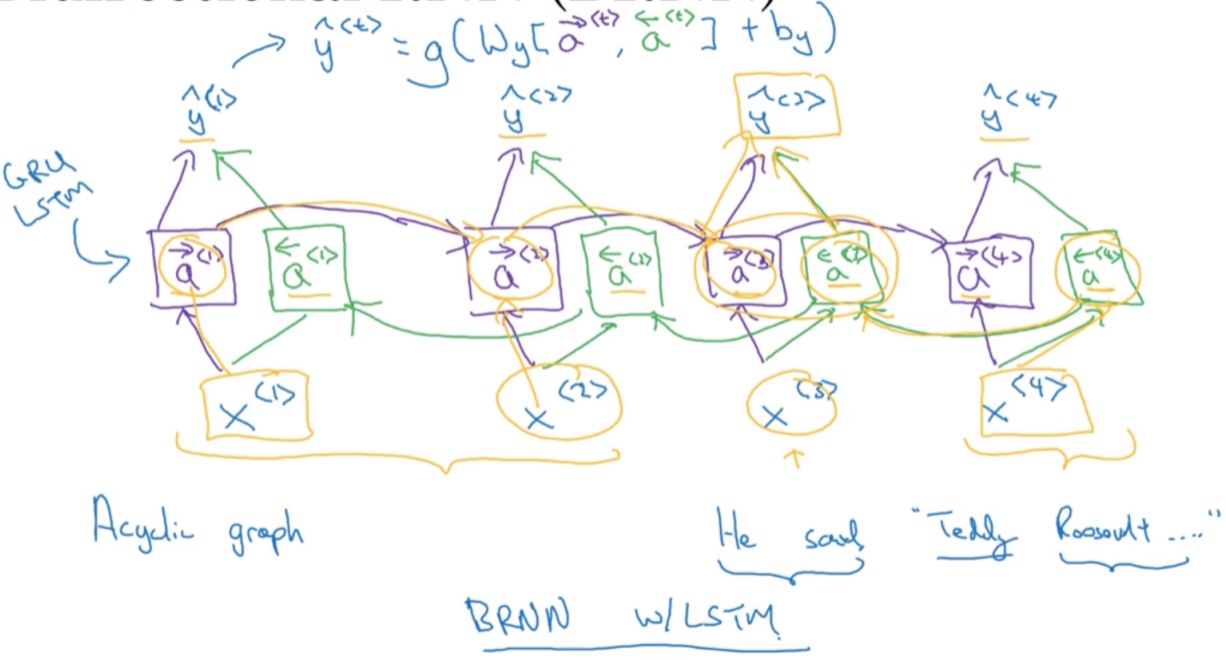所谓的Bi-LSTM以及Bi-RNN, 可以看成是两层神经网络, 第一层从左边作为系列的起始输入, 在文本处理上可以理解成从句子的开头开始输入, 而第二层则是从右边作为系列的起始输入, 在文本处理上可以理解成从句子的最后一个词语作为输入, 反向做与第一层一样的处理处理, 最后对得到的两个结果进行处理.

命名实体识别:

He said, ‘Teddy bears are on sales’

He said, ‘Teddy Roosevelt was a good man’

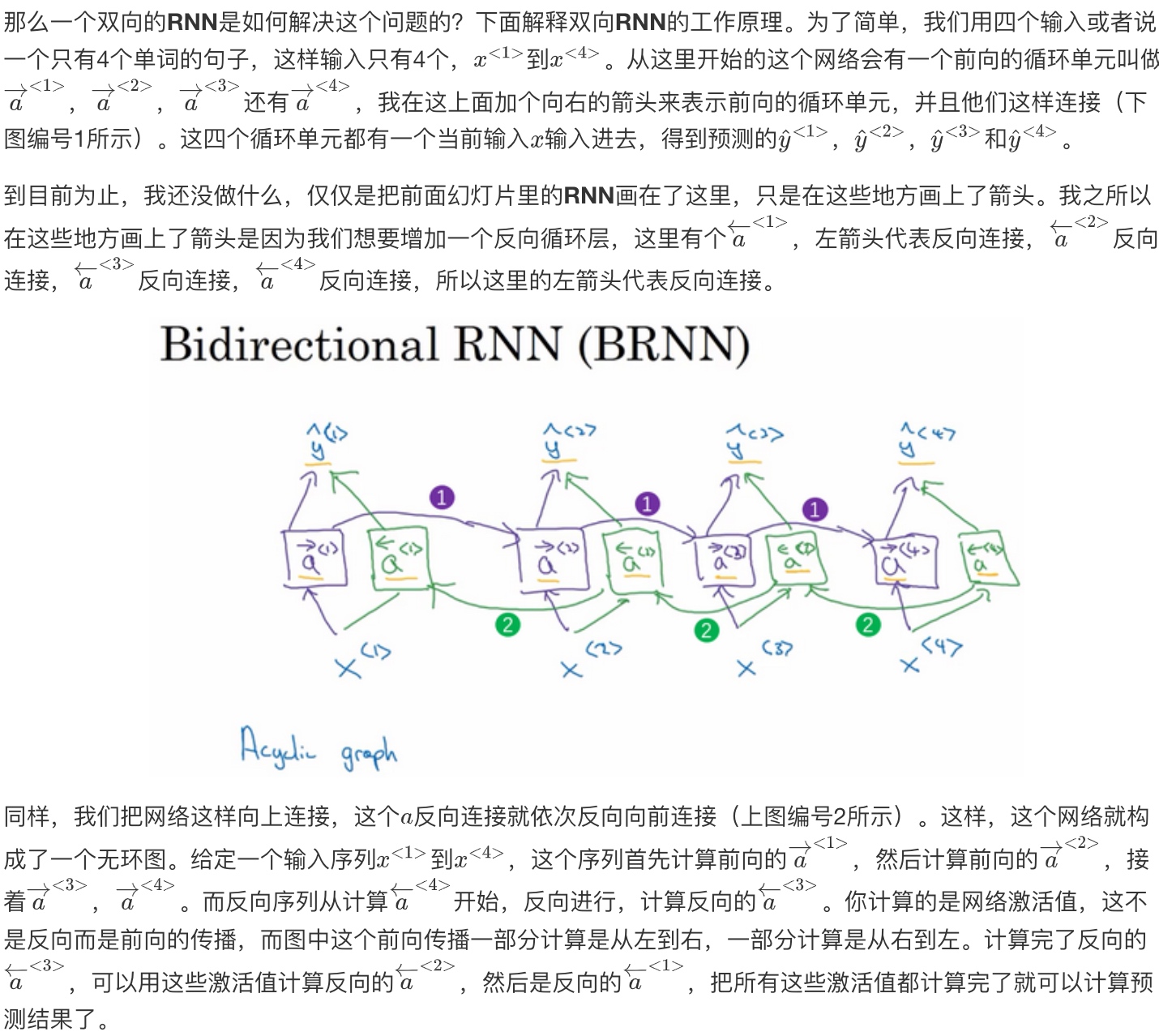
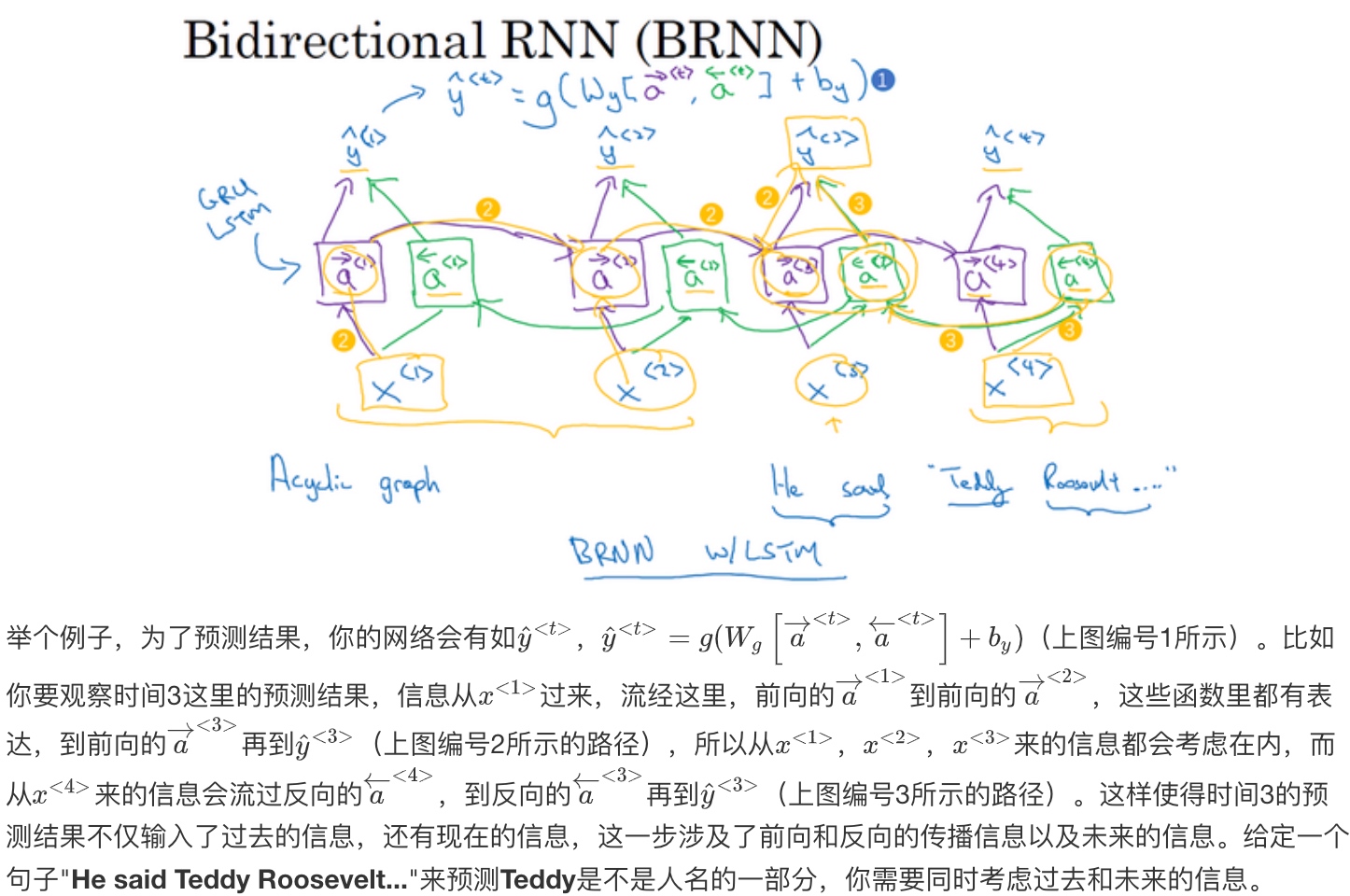
基本单元不仅仅是标准RNN单元，也可以是GRU单元或者LSTM单元。 事实上，很多的NLP问题，对于大量有自然语言处理问题的文本，有LSTM单元的双向RNN模型是用的最多的.

双向RNN网络模型的缺点就是你需要完整的数据的序列，才能预测任意位置. (例如语音识别需要等人说完才可以开始识别)

深层循环神经网络（Deep RNNs）

一层层往上叠加.

$a^{[1]<1>}$表示第一层第一个时间点的激活值.

具体来看, 激活值$a^{[2]<3>}$有两个输入，一个是从下面过来的输入$a^{[1]<2>}$, 还有一个是从左边过来的输入$a^{[2]<2>}$, 所以$a^{[2]<3>} = g(W_a^{[2]}[a^{[2]<2>},a^{[1]<3>}] + b_a^{[2]})$

每个单元没必要非是标准的RNN模型, 可以是GRU单元或者LSTM单元.

你可能见过很深的标准神经网络(100层以上), 而对于RNN来说, 有三层就已经不少了. 由于时间的维度, RNN网络会变得相当大.

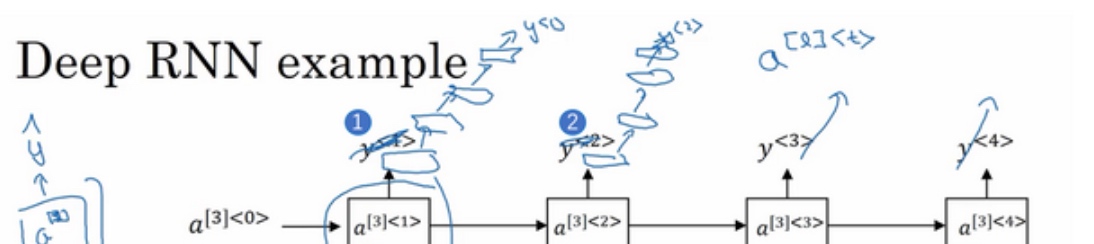
但是, 另一种常见架构可能是, 在每一个上面堆叠循环层，把输出去掉（上图编号1所示），然后换成一些深的层，这些层并不水平连接，只是一个深层的网络，然后用来预测$y^{<1>}$.

Ref:

• https://zhuanlan.zhihu.com/p/40119926
• http://colah.github.io/posts/2015-08-Understanding-LSTMs/