12. Special applications: Face recognition &Neural style transfer
什么是人脸识别?(What is face recognition?)
人脸验证(face verification)和人脸识别(face recognition) Verification:
- Input image, name/ID
- Output whether the input image is that of the claimed person (1对1问题)
Recognition:
- Has a database of K persons (1对多问题)
- Get an input image
- Output ID if the image is any of the K persons (or “not recognized”)
如果在验证系统(K=1), 准确率是99%; 在识别系统中(K=100). 如果每个人验证犯错的概率是1%, 那么识别犯错的就会就会是100倍.
One-Shot学习(One-shot learning)
人脸识别所面临的一个挑战就是需要解决一次学习问题,这意味着在大多数人脸识别应用中,需要通过单单一张图片或者单单一个人脸样例就能去识别这个人.
One-shot learning
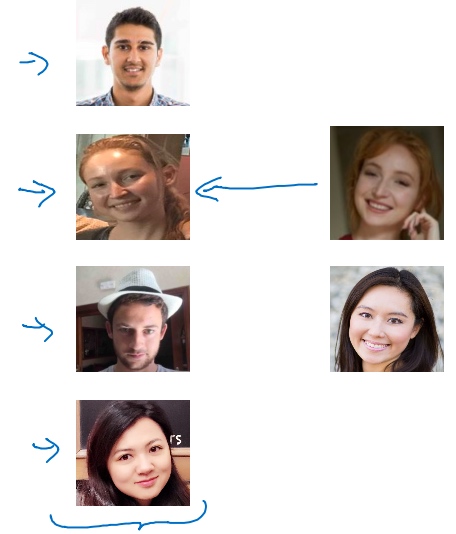
在一次学习问题中,只能通过一个样本进行学习,以能够认出同一个人。大多数人脸识别系统都需要解决这个问题,因为在数据库中每个人可能都只有一张照片.
One way it to learn from one example to recognize the person again. (将人的照片放进卷积神经网络中,使用softmax单元来输出每个人) 但是
- 如此小的训练集不足以去训练一个稳健的神经网络
- 每次加入一个新的人需要重新训练模型
所以, 真正有效的方式是Learning a “similarity” function (学习Similarity函数)
- d(img1,img2) = degree of difference between images
- 以两张图片作为输入,然后输出这两张图片的差异值
- If d(img1,img2) ≤ τ ===> ‘Same’
- If d(img1,img2) > τ ===> ‘Different’
- 将新的照片加入数据库,系统依然能照常工作
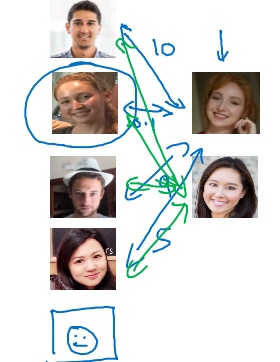
Siamese 网络(Siamese network)
[Taigman et. al., 2014. DeepFace closing the gap to human level performance], 他们开发的系统叫做DeepFace.
实现检测相似度的一个方式就是用Siamese网络.
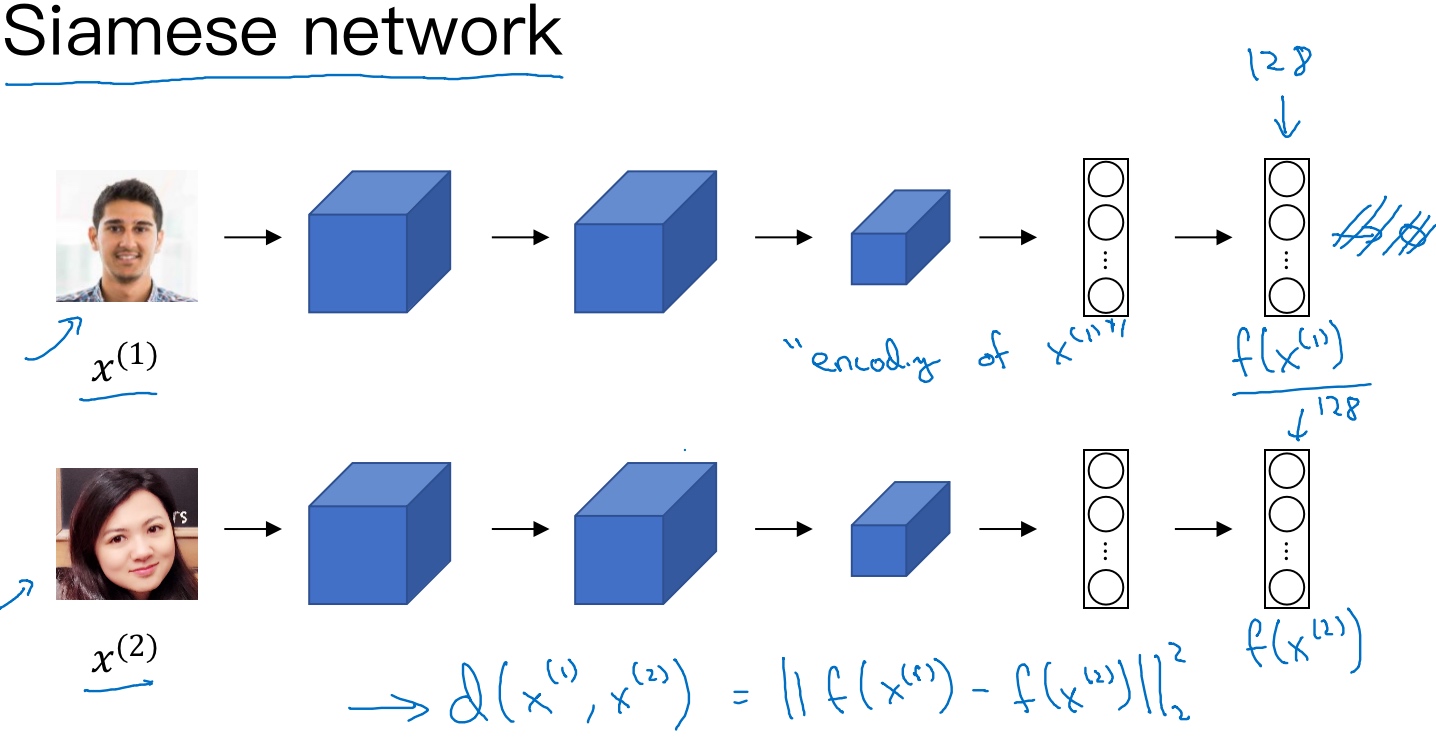
输入图像$x^{(1)}$, 经过卷积神经网络, 最后全连接层输出128维的向量 (不送进softmax做分类).
把这128个数命名$f(x^{(1)})$, 可以把它看作是输入图像的编码.
建立一个人脸识别系统的方法就是比较两个图片, 把第二张图片喂给有同样参数的同样的神经网络,然后得到一个不同的128维的向量(二张图片的编码$f(x^{(2)})$)
定义d, 将$x^{(1)},x^{(2)}$的距离定义为这两幅图片的编码之差的范数, $d(x^{(1)},x^{(2)}) = ||f(x^{(1)})-f(x^{(2)})||^2_2$
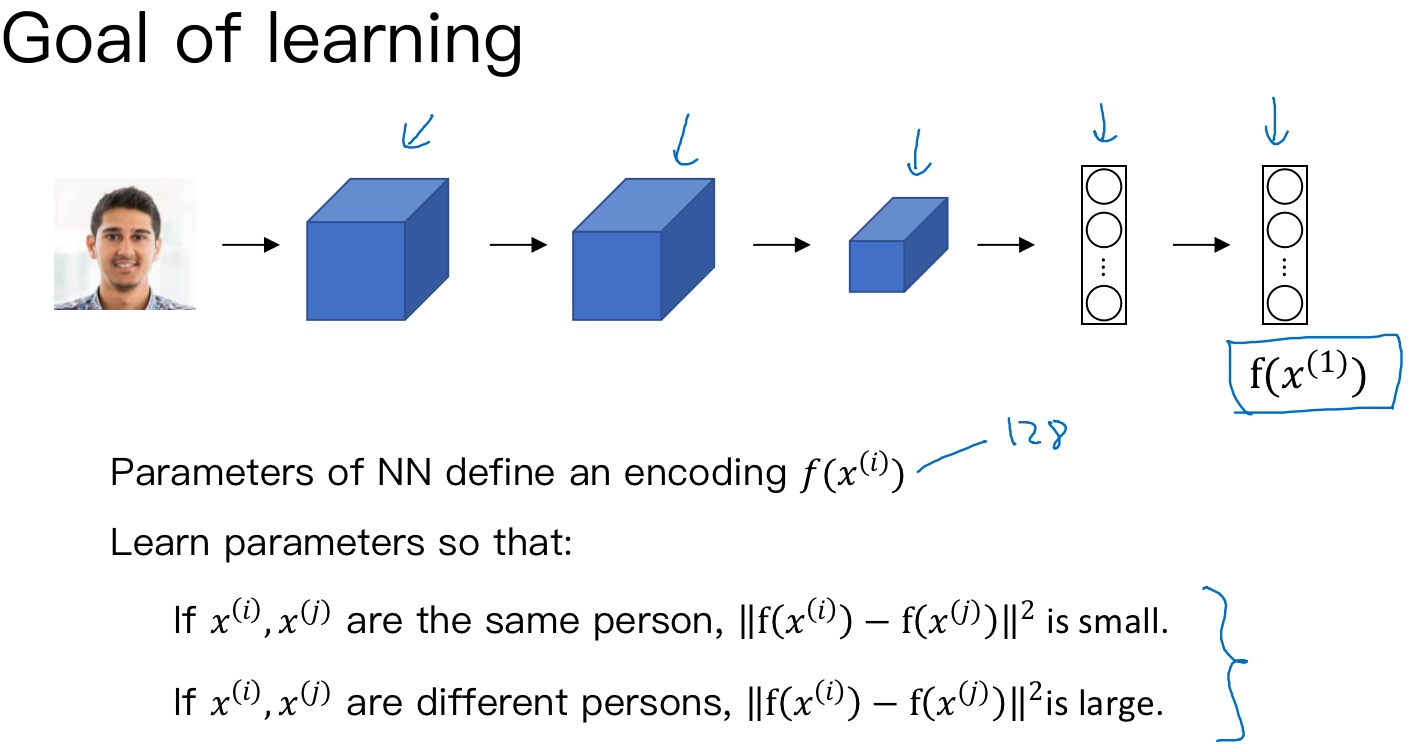
所以实际要做的就是训练一个网络(学习参数),它计算得到的编码可以用于函数d,它可以告诉两张图片是否是同一个人. 更准确地说,神经网络的参数定义了一个编码函数$f(x^{(i)})$,如果给定输入图像$x^{(i)},x^{(j)}$,这个网络会输出的128维的编码. 如果两个图片是同一个人,那么得到的两个编码的距离就小.
Triplet 损失(Triplet Loss)
[Schroff et al.,2015, FaceNet: A unified embedding for face recognition and clustering]
通过学习神经网络的参数来得到优质的人脸图片编码,方法之一就是定义三元组损失函数然后应用梯度下降
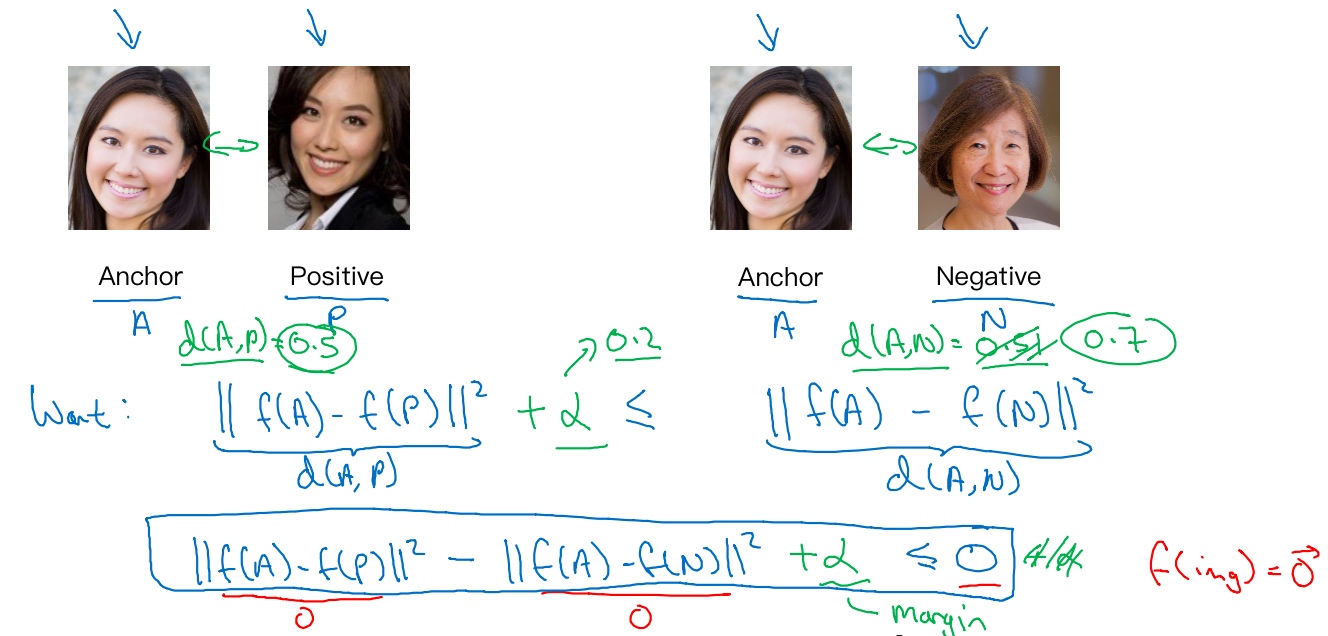
三元组损失,它代表通常会同时看三张图片,需要看Anchor图片、Postive图片(e意味着是同一个人),还有Negative图片(意味着是非同一个人), 简写成(A,P,N)
网络的参数或者编码能够满足以下特性:
$d(A,P)=||f(A) - f(P)||^2$,$d(A,N)=||f(A) - f(P)||^2$- 我们希望
$||f(A) - f(P)||^2$的数值很小 - 准确地说, 是希望
$||f(A) - f(P)||^2 \le ||f(A) - f(N)||^2$ - 所以
$||f(A) - f(P)||^2 - ||f(A) - f(N)||^2 \le 0$ - 如果所有图像f的都是一个零向量, 那么总能满足这个方程, 但是这是没有用处的. 所以为了确保网络对于所有的编码不会总是输出0 或者 互相相等的, 所以不能是刚好小于等于0, 应该小于一个-a值, 它也叫做间隔(margin)
$||f(A) - f(P)||^2 - ||f(A) - f(N)||^2 \le -a$- 修改后得到,
$||f(A) - f(P)||^2 - ||f(A) - f(N)||^2 + a \le 0$ - 假设a=0.2 (a是超参数),
$d(A,P)=0.5, d(A,N)=0.51$- 虽然0.51也是大于0.5的, 但是不够, 需要
$d(A,P)$比$d(A,N)$大很多
- 虽然0.51也是大于0.5的, 但是不够, 需要
定义损失函数:
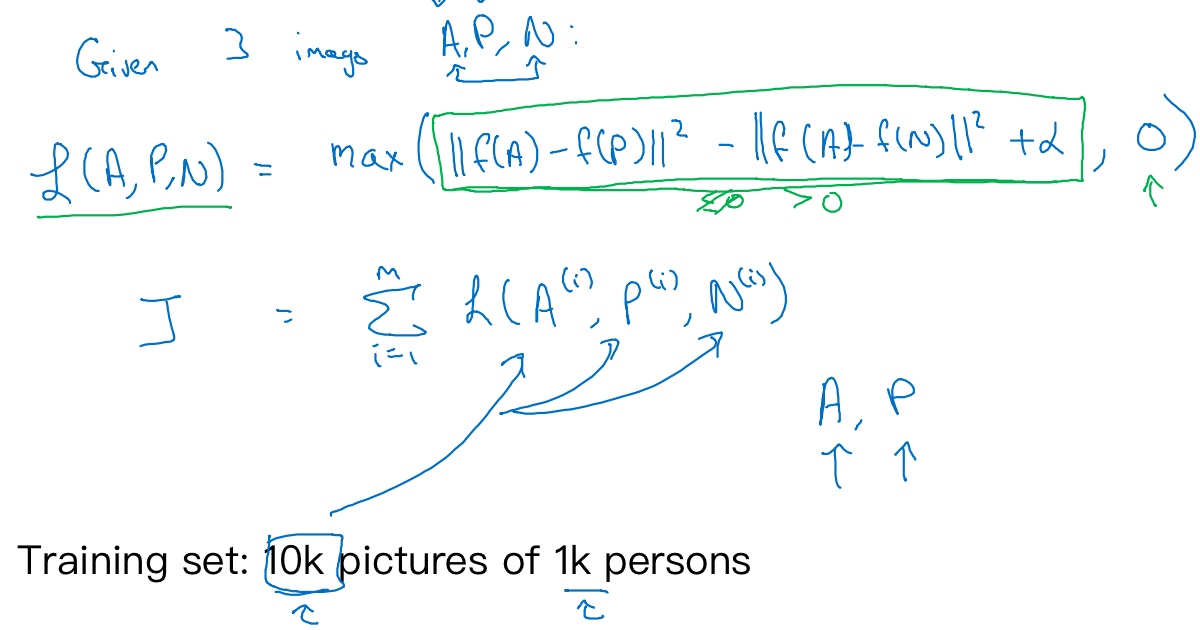
三元组损失函数的定义基于三元图片组(A,P,N).
$L(A,P,N) = max(||f(A) - f(P)||^2 - ||f(A) - f(N)||^2 + a , 0)$- 只要能使
$||f(A) - f(P)||^2 - ||f(A) - f(N)||^2 + a$小于等于0, 那么这个例子的损失就是0, 神经网络不会关心它负值有多大网络不会关心它负值有多大 - 整个网络的代价函数应该是训练集中单个三元组损失的总和
- 假设有10000个图片的训练集,里面是1000个不同的人的照片(平均每个人10张照片, 只有有每个人一张照片, 根本没法训练这个系统),要做的就是取这10000个图片,然后生成这样的三元组,然后训练学习算法,对这种代价函数用梯度下降
- 注意,为了定义三元组的数据集需要成对的A和P,即同一个人的成对的图片
如何选择这些三元组来形成训练集
[Schroff et al.,2015, FaceNet: A unified embedding for face recognition and clustering]

随机地选择A,P,N, 遵守A和P是同一个人,而A和N是不同的人这一原则.
但是随机选择, $d(A,P) < d(A,N)$这个约束条件很容易达到, A,N比A,P差别很大的概率很大.
所以为了构建一个数据集,要做的就是尽可能选择难训练的三元组A,P,N. 就是$d(A,P)$尽量很接近$d(A,N)$ ==> $d(A,P) \approx d(A,N)$, 这样学习算法会竭尽全力使右边这个式子$d(A,N)$变大, 或者使左边这个式子$d(A,P)$变小
果随机的选择这些三元组,其中有太多会很简单,梯度算法不会有什么效果,因为网络总是很轻松就能得到正确的结果,只有选择难的三元组梯度下降法才能发挥作用,使得这两边离得尽可能远
Example:

人脸验证与二分类(Face verification and binary classification)
Triplet loss是一个学习人脸识别卷积网络参数的好方法, 但是还有其他学习参数的方法 - 将人脸识别当成一个二分类问题
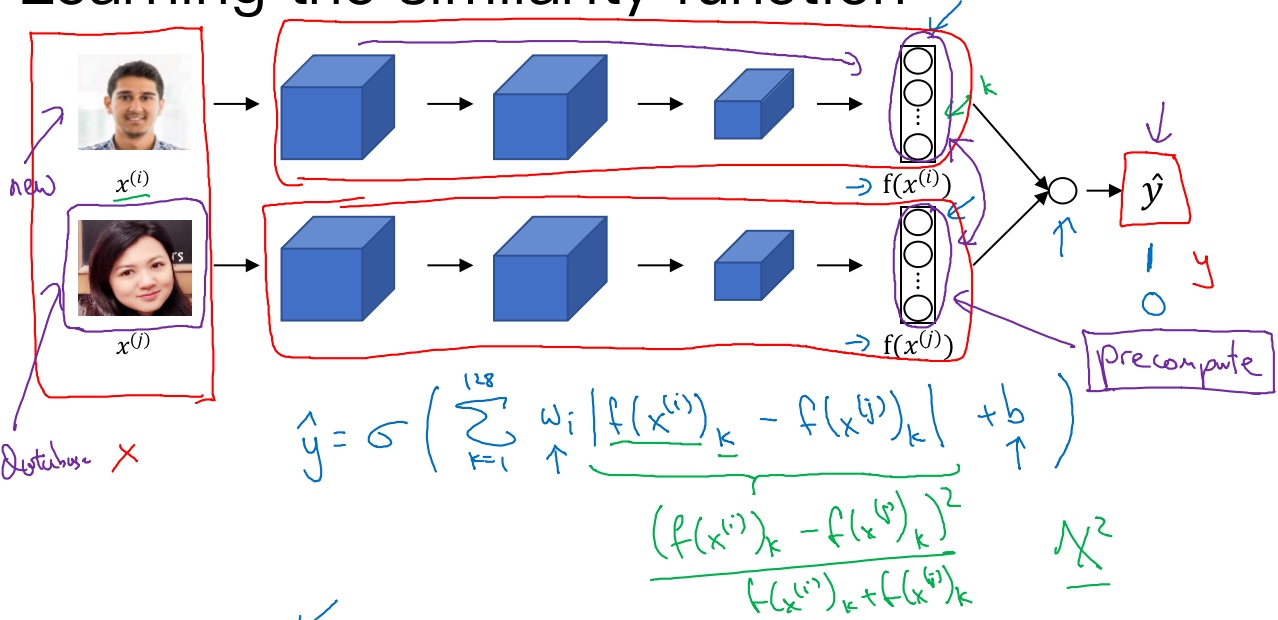
选取一对神经网络(Siamese网络), 使其同时计算嵌入, 比如说128维的嵌入$f(x^{(i)})$, 然后将其输入到逻辑回归单元,然后进行预测,如果是相同的人,输出是1; 若是不同的人, 输出是0.
最后的输出$\tilde{y}$利用了编码之间的不同, $\tilde{y} = \sigma(\sum_{k=1}^{128} w_i|f(x^{(i)})_k - f(x^{(j)})_k| + b)$
- 符号
$f(x^{(i)})_k$代表图片$x^{(i)}$的编码,下标k代表选择这个向量中的第k个元素 - 把这128个元素当作特征放入逻辑回归中, 逻辑回归可以增加参数w和b (就像普通的逻辑回归). 将在这128个单元上训练出合适的权重, 用来预测两张图片是否是一个人 (0 or 1)
还有其他不同的形式来计算上图绿色标记的公式, 比如说公式可以是:
$\frac{(f(x^{(i)})_k - f(x^{(j)})_k)^2}{(f(x^{(i)})_k + f(x^{(j)})_k)^2} $, 这个公式也被叫做$\chi$公式 或者 $\chi$平方相似度
注: 可以运用预先计算的思想节省大量的计算. 只需要计算新的编码, 然后和预先计算好编码进行比较,最后输出预测值$\tilde{y}$
Face verification supervised learning:

什么是神经风格迁移?(What is neural style transfer?)
Neural style transfer

为了实现神经风格迁移,需要知道深层的、浅层的卷积网络如何提取的特征
CNN特征可视化(What are deep ConvNets learning?)
[Zeiler and Fergus., 2013, Visualizing and understanding convolutional networks]
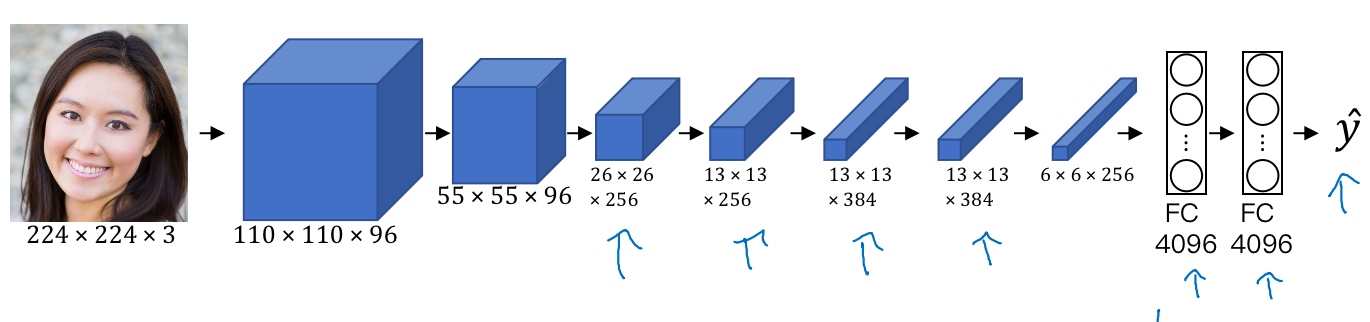
假如训练了一个卷积神经网络(Alexnet, 轻量级网络), 希望将看到不同层之间隐藏单元的计算结果, 做法:
- Pick a unit in layer 1. Find the nine image patches that maximize the unit’s activation.
- Repeat for other units.
从第一层的隐藏单元开始,假设遍历了训练集,然后找到那些使得单元激活最大化的一些图片/图片块 (将训练集经过神经网络,然后弄明白哪一张图片最大限度地激活特定的单元)
选择一个隐藏单元,发现有9个图片最大化了单元激活,可能找到这样的9个图片块(编号1),似乎是图片浅层区域显示了隐藏单元所看到的,找到了像这样的边缘或者线(编号2),这就是那9个最大化地激活了隐藏单元激活项的图片块:
 ==>
==> 
以此类推,最后得到9个不同的代表性神经元,每一个不同的图片块都最大化地激活了 (第一层的隐藏单元通常会找一些简单的特征,比如说边缘或者颜色阴影)

CNN从检测简单的事物,比如说,第一层的边缘,第二层的质地,到深层的复杂物体.
代价函数(Cost function)
[Gatys et al., 2015. A neural algorithm of artistic style. Images on slide generated by Justin Johnson]
通过最小化代价函数, 可以生成任何神经风格迁移图像, 所以要事先定义一个代价函数.
Neural style transfer cost function:

- 内容图像C
- 给定一个风格图片S
- 目标是生成一个新图片G
为了实现神经风格迁移,要做的是定义一个关于G的代价函数J用来评判某个生成图像的好坏, 然后使用梯度下降法去最小化J(G)
这个代价函数定义为两个部分:
$J_{content}(C,G)$- 内容代价, 用来度量生成图片G的内容与内容图片C的内容有多相似
$J_{style}(S,G)$- 把内容代价的结果加上一个风格代价函数, 用来度量生成图片G的风格和风格图片S的风格的相似度
最后, 最后用两个超参数$\alpha, \beta$来确定内容代价和风格代价, $J(G) = \alpha J_{content}(C,G) + \beta J_{content}(S,G)$
Find the generated image G:

- 随机初始化生成图像G
- 使用梯度下降的方法将J(G)最小化
$G:= G- \frac{\delta}{\delta G} J(G)$
最后慢慢生成右边图片, 使G逐渐有C的内容和G的风格.
内容代价函数(Content cost function)
$J(G) = \alpha J_{content}(C,G) + \beta J_{content}(S,G)$
流程:
- Say you use hidden layer l to compute content cost. (用隐含层l来计算内容代价, 通常l会选择在网络的中间层)
- CNN的每个隐藏层分别提取原始图片的不同深度特征,由简单到复杂。如果l太小,则G与C在像素上会非常接近,没有迁移效果;如果l太深,则G上某个区域将直接会出现C中的物体。因此,l既不能太浅也不能太深,一般选择网络中间层
- Use pre-trained ConvNet. (E.g., VGG network) (用一个预训练的卷积模型)
- Let
$a^{[l](C)}$and$a^{[l](G)}$be the activation of layer l on the images ($a^{[l](C)},a^{[l](G)}$分别代表两个图片C和G的l层的激活函数值) - If
$a^{[l](C)}$and$a^{[l](G)}$are similar, both images have similar content (比较, 如果这两个激活值相似,那么就意味着两个图片的内容相似($ J_{content}(C,G)$越小))
定义这个
$ J_{content}(C,G) = \frac{1}{2}||a^{[l](C)} - a^{[l](G)}||^2$
取l层的隐含单元的激活值,按元素相减,内容图片的激活值与生成图片相比较,然后取平方,也可以在前面加/不加上归一化或者$/frac{1}{2}$, 都影响不大, 因为最后都可以由Jcontect的超参数$\alpha$来调整.
风格代价函数(Style cost function)
[Gatys et al., 2015. A neural algorithm of artistic style]
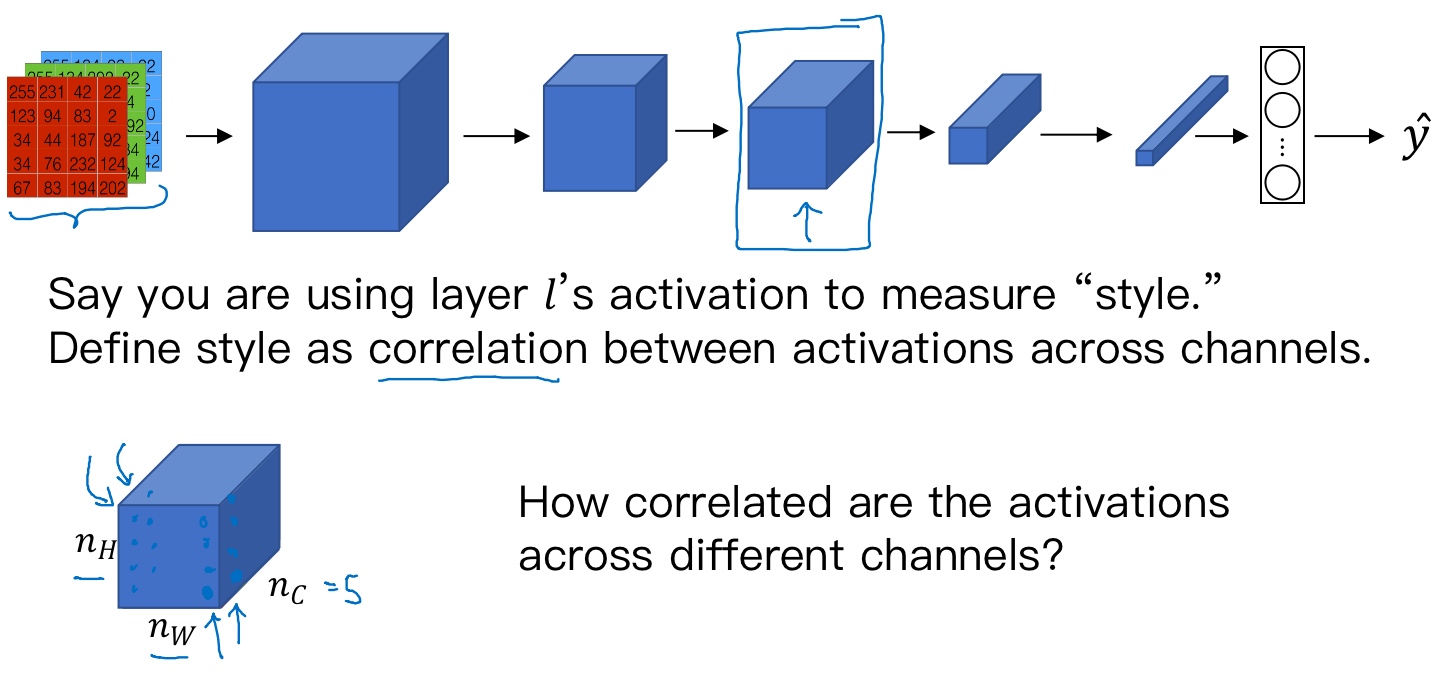
- Say you are using layer l’s activation to measure “style.”
- Define style as correlation between activations across channels. (将图片的风格定义为l层中各个通道之间激活项的相关系数(乘积))

将l层的激活项取出,这是个$n_H \times n_W \times n_C$的激活项,它是一个三维的数据块.
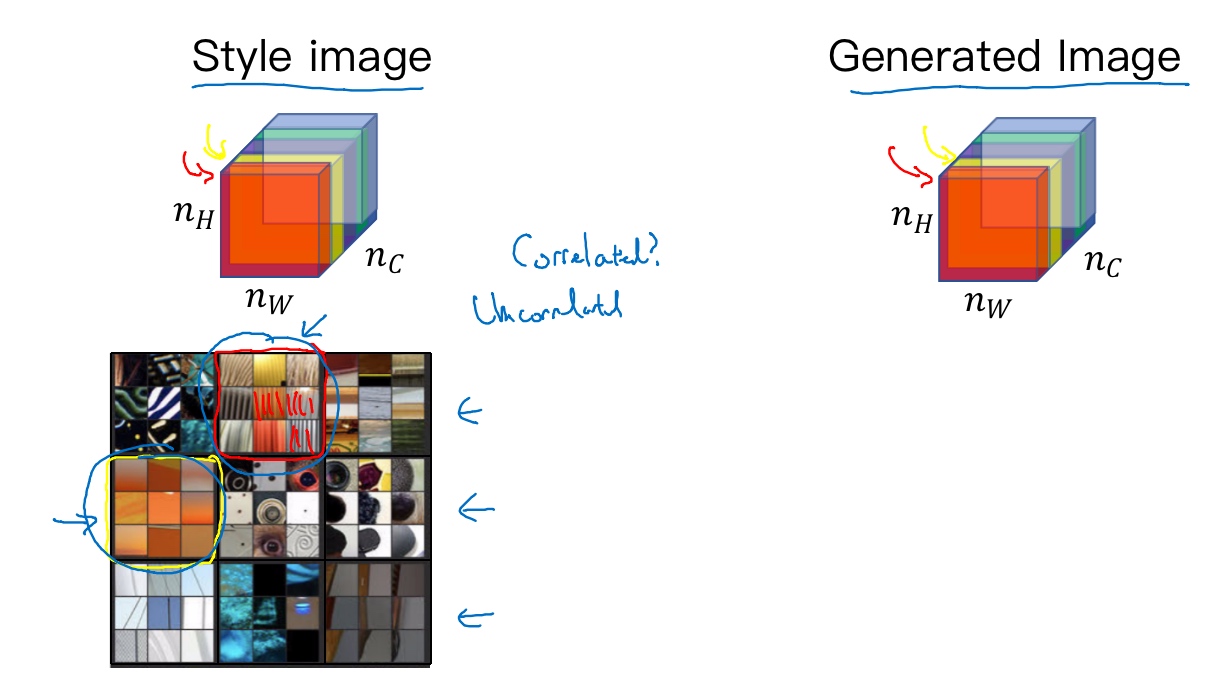
假设把它的不同通道渲染成不同的颜色(这里假设5种/5通道)
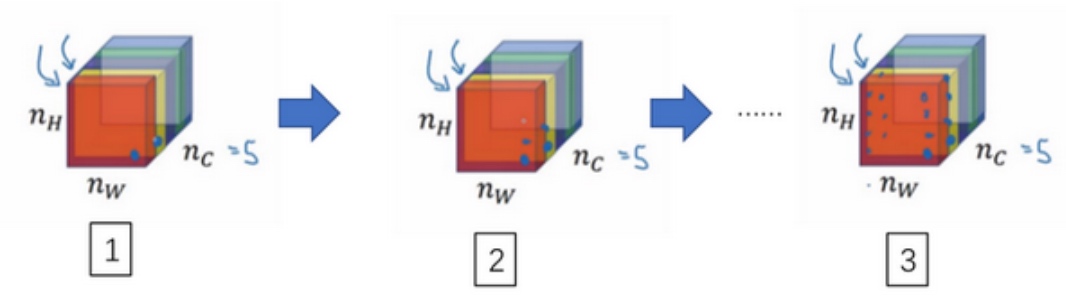
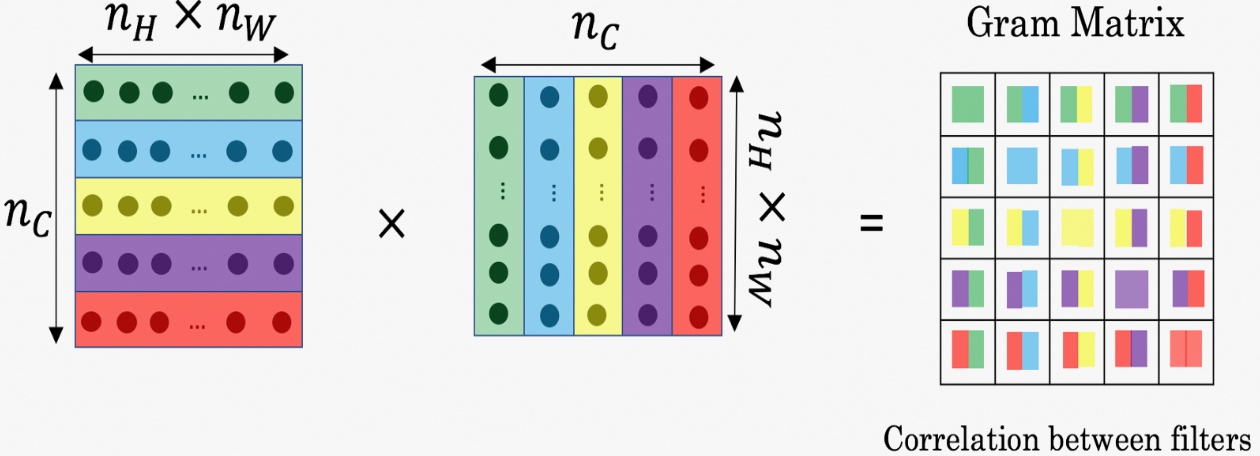
如编号1所示, 在第一个通道(右下角处)中含有某个激活项,第二个通道也含有某个激活项,于是它们组成了一对数字. 其他同理, 最后会取得$n_H \times n_W $的通道中所有的数字对, 然后就可以计算它们的相关系数
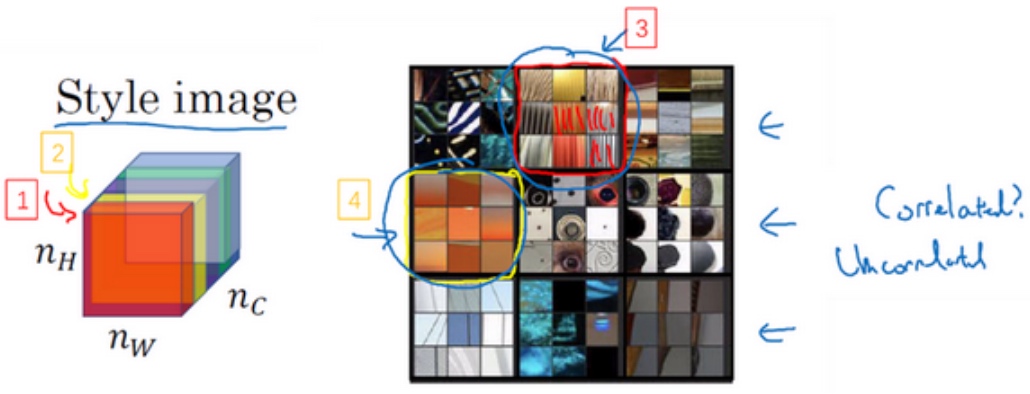
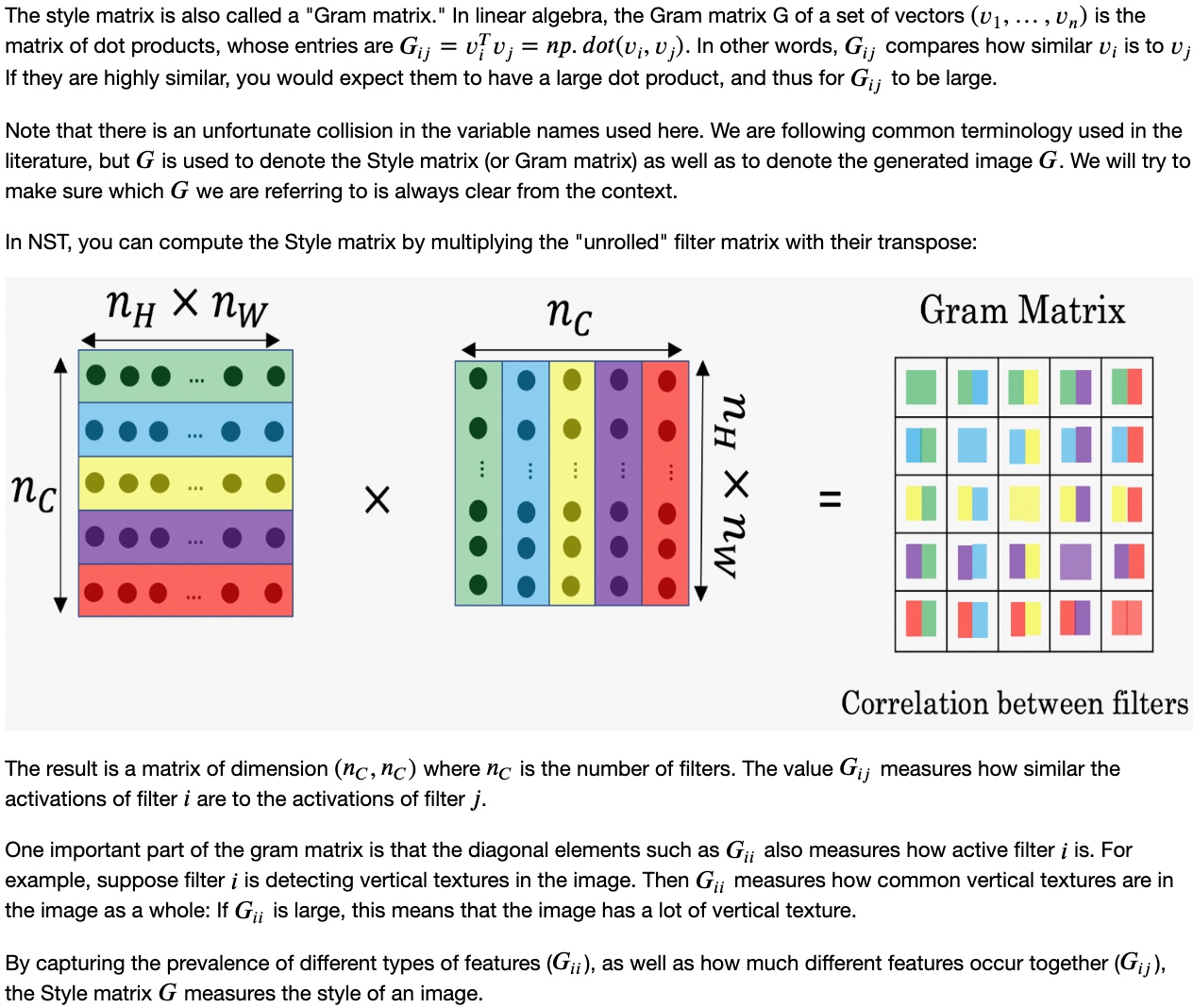
例如我们选取第$l$层隐藏层,其各通道使用不同颜色标注(如下图所示). 因为每个通道提取图片的特征不同,比如1通道(红色)提取的是图片的垂直纹理特征,2通道(黄色)提取的是图片的橙色背景特征。那么计算这两个通道的相关性大小,相关性越大,表示原始图片及既包含了垂直纹理也包含了该橙色背景;相关性越小,表示原始图片并没有同时包含这两个特征。也就是说,计算不同通道的相关性,反映了原始图片特征间的相互关系,从某种程度上刻画了图片的“风格”。
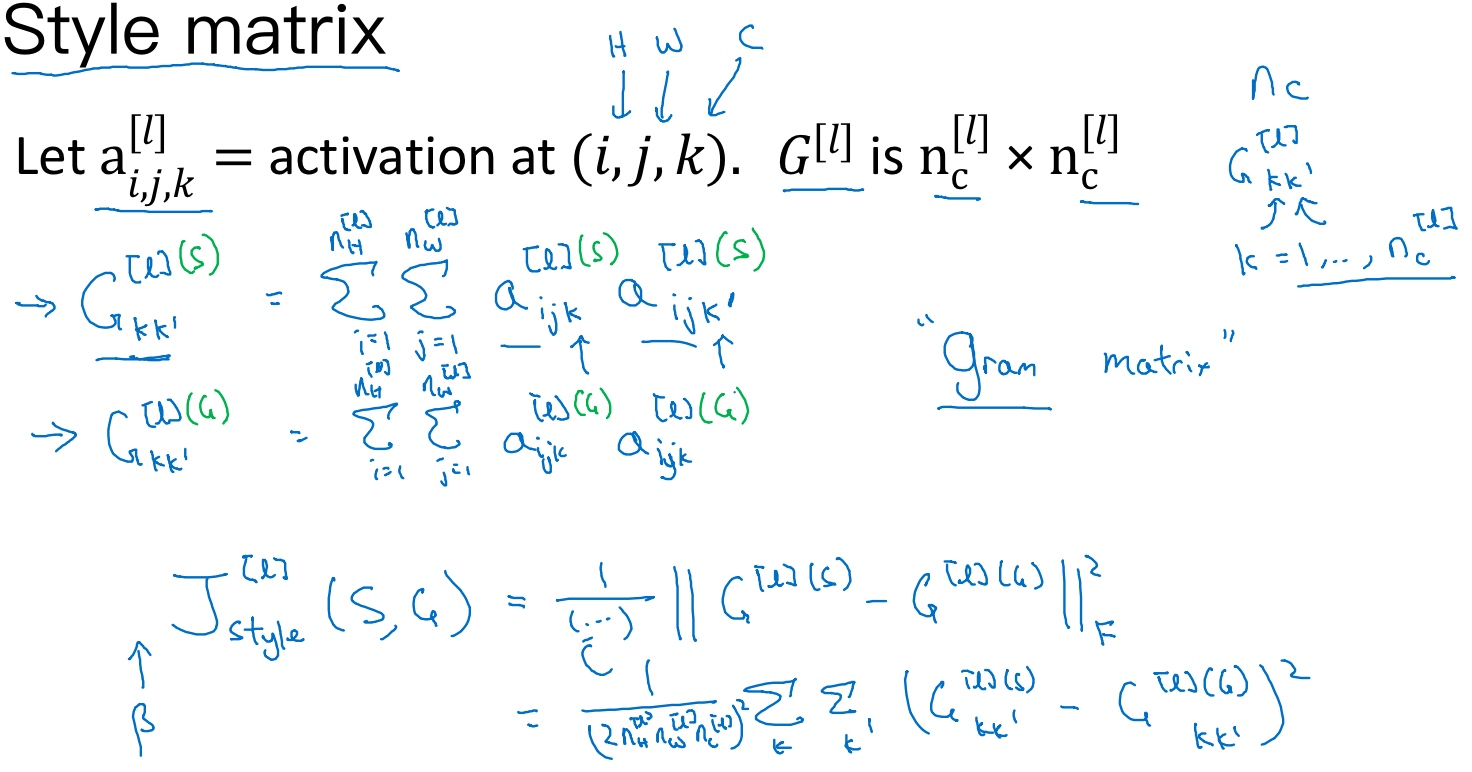
设$a^{[l]}_{i,j,k}$为隐藏层l中(i,j,k)位置的激活项, 分别代表该位置的高度、宽度以及对应的通道数.
- 计算一个关于l层和风格图像的矩阵
$G^{[l](S)}$(l示层数, S表示风格图像, 它是个$n_C \times n_C$的矩阵) - 在这个矩阵中
$k, k^{\prime}$元素被用来描述通道$k$和$k^{\prime}$通道之间的相关系数:$G^{[l](S)}_{k,k^{\prime}} = \sum^{n^{[l]}_H}_{i=1}\sum^{n^{[l]}_W}_{j=1}a^{[l](S)}_{i,j,k}a^{[l](S)}_{i,j,k^{\prime}} $用符号i,j表示下界,对$i,j,k$位置的激活项$a^{[l]}_{i,j,k}$,乘以同样位置的激活项,也就是$i,j,k^{\prime}$位置的激活项,即,将它们两个相乘。然后和分别加到l层的高度和宽度,即和,将这些不同位置的激活项都加起来。和中坐标和坐标分别对应高度和宽度,将通道和通道上这些位置的激活项都进行相乘。- 严格来说,它是一种非标准的互相关函数,因为没有减去平均数,而是将它们直接相乘
接下来我们就可以定义图片的风格矩阵(style matrix)为:
$$G^{[l](S)}_{k,k^{\prime}} = \sum^{n^{[l]}_H}_{i=1}\sum^{n^{[l]}_W}_{j=1}a^{[l](S)}_{i,j,k}a^{[l](S)}_{i,j,k^{\prime}} $$
其中,
$[l]$表示第$l$层隐藏层,$k,k’$分别表示不同通道,总共通道数为$n^{[l]}_C$.$i,j$分别表示该隐藏层的高度和宽度.- 风格矩阵
$G^{[l]}_{kk′}$计算第$l$层隐藏层不同通道对应的所有激活函数输出和.- 即, 将
$k,k’$通道上对应的激活项进行相乘, 然后将这些不同位置的激活项都加起来 - 严格来说,它是一种非标准的互相关函数,因为没有减去平均数,而是将它们直接相乘
- 即, 将
$G^{[l]}_{kk′}$的维度为$n^{[l]}_c \times ^{[l]}_c$.- 若两个通道之间相似性高,则对应的
$G^{[l]}_{kk′}$值较大;若两个通道之间相似性低,则对应的$G^{[l]}_{kk′}$值较小.
风格矩阵$G^{[l](S)}_{k,k^{\prime}}$表征了风格图片S第$l$层隐藏层的“风格”。相应地,生成图片G也有$G^{[l](G)}_{k,k^{\prime}}$. 那么,$G^{[l](S)}_{k,k^{\prime}}$与$G^{[l](G)}_{k,k^{\prime}}$越相近,则表示G的风格越接近S (所以是要最小化它们的误差). 这样,我们就可以定义出代价函数$J^{[l]}_{style}(S,G)$的表达式:
$$J^{[l]}_{style}(S,G) = \frac{1}{2n^{[l]}_{H}n^{[l]}_{W}n^{[l]}_{C}}\sum^{n^{[l]}_C}_{k=1}\sum^{n^{[l]}_C}_{k^{\prime}=1} ||G^{[l](S)}_{k,k^{\prime}} - G^{[l](G)}_{k,k^{\prime}}||^2_F $$
- 由于是计算两个矩阵之间的误差, 所以用了Frobenius范数 (计算两个矩阵对应元素相减的平方的和)
- 这里使用了一个归一化常数,
$\frac{1}{2n^{[l]}_{H}n^{[l]}_{W}n^{[l]}_{C}}$

定义完$J^{[l]}_{style}(S,G)$之后,我们的目标就是使用梯度下降算法,不断迭代修正G的像素值,使$J^{[l]}_{style}(S,G)$不断减小。
以上只比较计算了一层隐藏层$l$. 为了提取的“风格”更多(对各层都使用风格代价函数,会让结果变得更好), 可以使用多层隐藏层, 然后把各个层的结果(各层的风格代价函数)相加, 表达式为:
$$J_{style}(S,G) = \sum_l \lambda^{[l]} J^{[l]}_{style}(S,G)$$
其中,
$\lambda^{[l]}$表示累加过程中各层$J^{[l]}_{style}(S,G)$的权重系数,为超参数.- 这样能够在神经网络中使用不同的层,包括之前的一些可以测量类似边缘这样的低级特征的层,以及之后的一些能测量高级特征的层,使得神经网络在计算风格时能够同时考虑到这些低级和高级特征的相关系数.
根据以上推导,最终的cost function为:
$$J(G) = \alpha J_{content}(C,G) + \beta J_{content}(S,G)$$
使用梯度下降算法进行迭代优化
一.神经风格迁移简介
二.计算content cost
三.计算style cost
一.神经风格迁移简介
1.神经风格迁移(Neural Style Transfer),简称为NST,就是以一张图为内容基础,以另一张图为风格基础,生成一张新的图:

2.NST使用一张已经训练好的神经网络VGG network作为算法的基础。可知神经网络的浅层学习一些比较低级的特征诸如边界和纹理的等,深层学些一些复杂抽象的特征。为了学习得比较精确但又不过于苛刻,我们一般选择VGG network的中间的隐藏层作为最后的输出(以此计算代价函数,然后进行反向传播)
3.NST的大概步骤是:
1)加载训练好的VGG神经网络
2)随机初始化生成图像G
3)输入内容图像C,进行前向传播,计算content cost;输入风格图像G,进行前向传播,计算style cost。最后统计总的cost
4)根据计算出的cost,进行反向传播,更新生成图像G的每个像素点
5)重复3)4)步一定的次数
6)输出最终的申城图像G
二.计算content cost
1.content cost,就是计算内容图像与生成图像的“内容差异”,所以直接是对应位置的差值。
2.在计算时,最好将每个信道展开成一个向量。此步骤不是必须的,但可以方便操作:
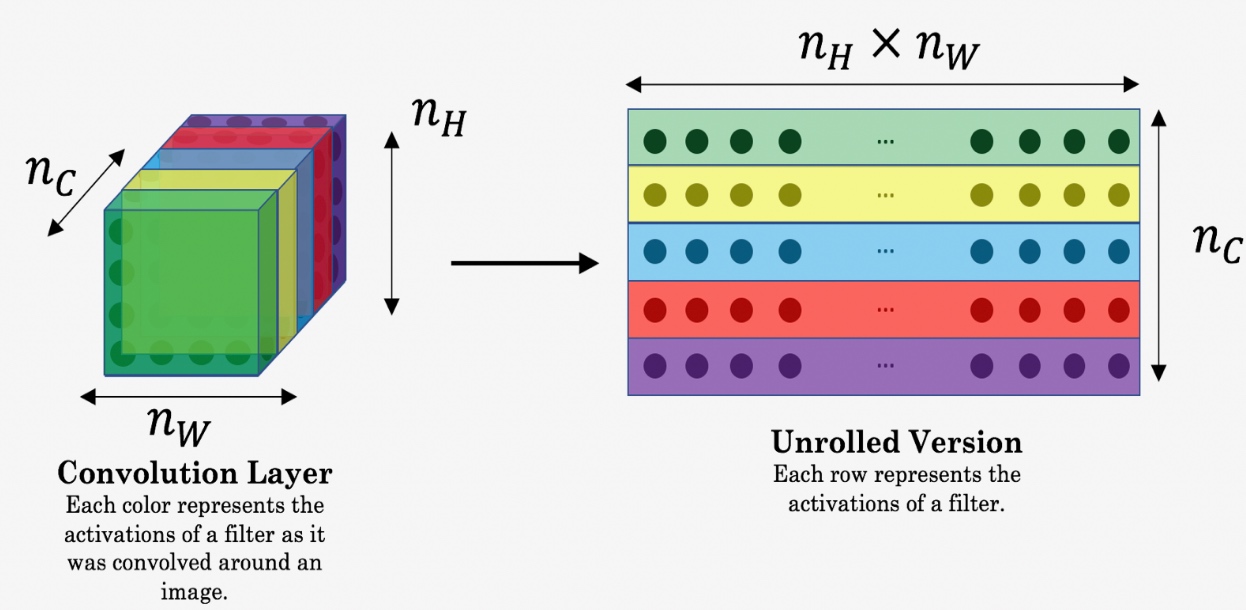
3.content cost的计算公式如下:
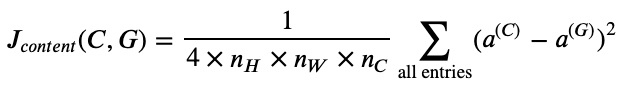
其中a为选中的VGG网络的隐藏层的输出值。
三.计算style cost
1.与content cost直接用对应位置与衡量不同,style cost似乎没有什么直接的衡量的依据。确实是没有,但是可以通过信道间接地去衡量。
2.据称,在同一个卷积层中,不同的信道学习的东西是不同的,比如:

第一个信道主要学习纹理特征、第二个信道主要学习橙色特征。如果在出现纹理的地方,其颜色总是为橙色,则表明信道一盒信道二有很强的的关联性。而提到关联性,就很自然能想到协方差矩阵。因此,风格可以用信道的协方差矩阵去衡量。同时说明,风格,实际上就是不同特征之间的关联度。
3.为了计算信道之间的协方差矩阵,最好将一个信道展开成一个向量,然后根据 A*AT的公式计算协方差矩阵:
最后,style的计算公式如下:
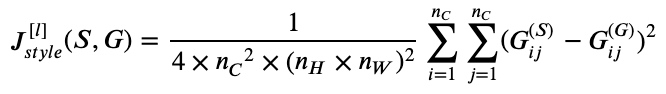
一维到三维推广(1D and 3D generalizations of models)
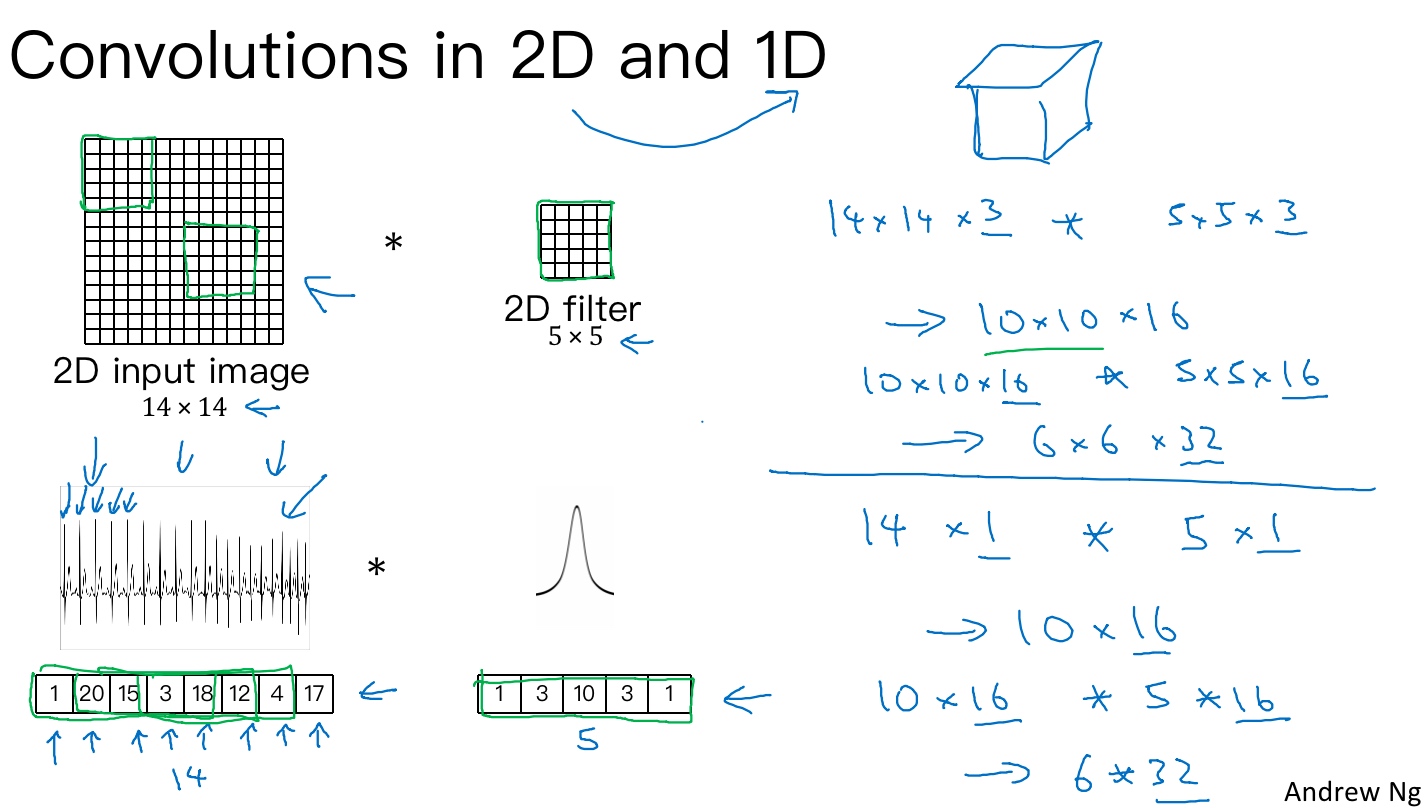
2D图片卷积的规则:
- 输入图片维度:14 x 14 x 3
- 过滤器尺寸:5 x 5 x 3,过滤器个数:16
- 输出图片维度:10 x 10 x 16
将2D卷积推广到1D卷积(心电图electrocardiogram(EKG)), 1D卷积的规则:
- 在胸部放置一个电极,电极透过胸部测量心跳带来的微弱电流,正因为心脏跳动,产生的微弱电波能被一组电极测量,这就是人心跳产生的EKG,每一个峰值都对应着一次心跳
- 输入时间序列维度:14 x 1
- 过滤器尺寸:5 x 1,过滤器个数:16
- 输出时间序列维度:10 x 16
- 可以在不同的位置使用相同的特征检测器.比如说,为了区分EKG信号中的心跳的差异,可以在不同的时间轴位置使用同样的特征来检测心跳
- 对于卷积网络的下一层, 如果输入一个10×16数据, 可以使用32个5维过滤器进行卷积, 这需要16个通道进行匹配, 另一层的输出结果就是6×32
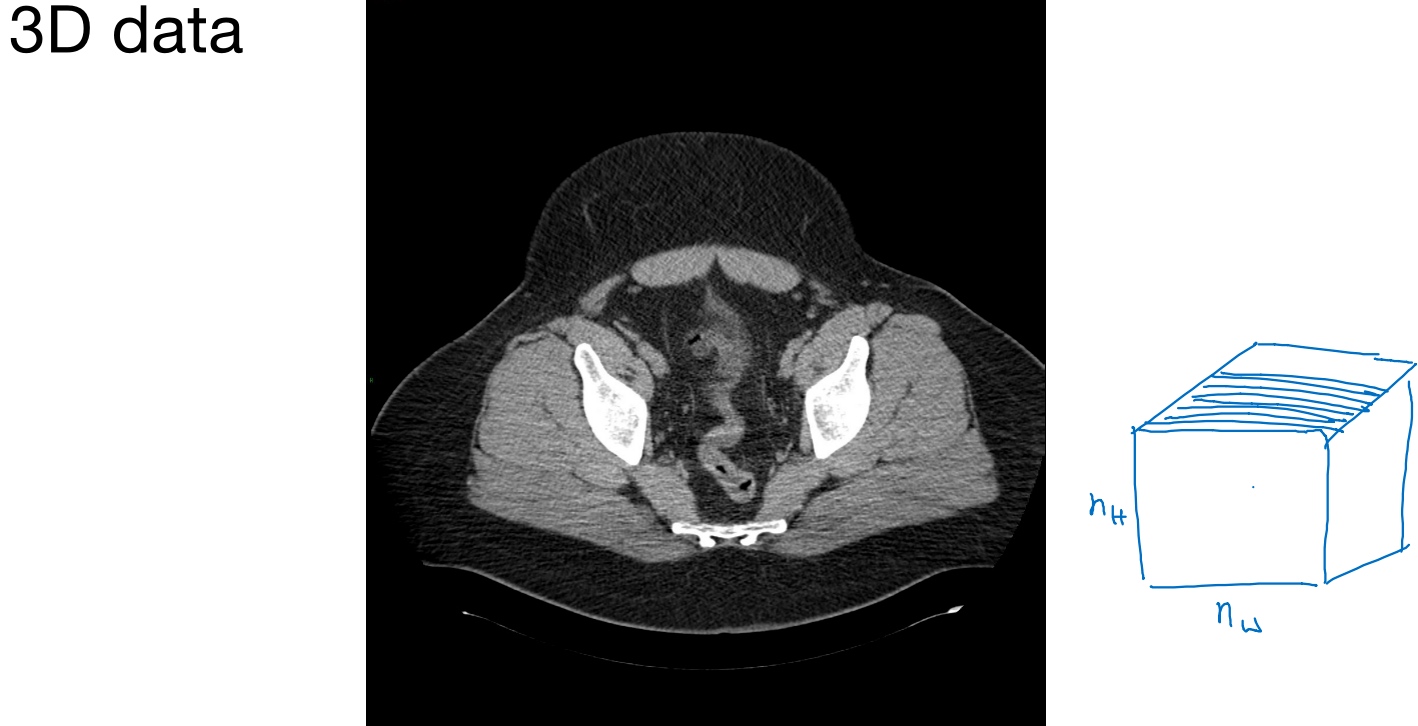
3D卷积(CT scan 大脑扫描图):
- 输入3D图片维度:14 x 14 x 14 x 1
- 3D对象不一定是一个完美立方体,所以长和宽可以不一样
- 过滤器尺寸:5 x 5 x 5 x 1,过滤器个数:16
- 输出3D图片维度:10 x 10 x 10 x 16

范数(Norm)
范数(Norm)是具有度量性质的函数,它经常使用来衡量矢量函数的长度或大小,是泛函分析中的一个基本概念。在赋范线性空间中,p范数定义如下
$||x||_p = (\sum_{i=1}^N |x_i|^p)^{\frac{1}{p}}$
其中, p∈R, p≥1.
范数具有3个性质,即
- 非负性;
- 齐次性;
- 三角不等式。
在机器学习中,会遇到一些范数:
$L_0$范数: 统计向量中非零元素的个数来衡量向量的大小. L0范数并不是一个真正的范数, 因此L1范数经常用作表示非零元素数目的替代函数.$L_1$范数:$║x║_1=│x_1│+│x_2│+…+│x^n│ = \sum_{i=1}^n |x_i|$- 曼哈顿距离、最小绝对误差等都是L1范数
- 可以用来度量两个向量间的差异, 如绝对误差和(Sum of Absolute Difference):
$SAD(x_1,x_2) = \sum_{i=1}^n |x_{1i} -x_{2i}|$
$L_2$范数:$║x║_2=(│x_1│^2+│x_2│^2+…+│xn│^2)^{1/2} = \sqrt{\sum_{i=1}^n x_i^2}$- 向量元素的平方和再开平方
- 用来度量距离, 欧氏距离就是一种L2范数
- 可以度量两个向量间的差异, 如平方差和(Sum of Squared Difference)):
$SSD(x_1,x_2) = \sum_{i=1}^n (x_{1i} -x_{2i})^2$ - L2范数通常会被用来做优化目标函数的正则化项,防止模型为了迎合训练集而过于复杂造成过拟合的情况,从而提高模型的泛化能力
$L_∞$范数:$║x║_∞=max(│x_1│,│x_2│,…,│x_n│)= max(|x_i|)$- 主要被用来度量向量元素的最大值
上述几种范数都是p范数的推导式,但是在机器学习中还有一类范数有些矩阵范数不可以由矢量范数来诱导,比如常用的Frobenius范数,其形式为
$║A║_F= \sqrt{\sum_i\sum_j a_{ij}^2}$- 矩阵A全部元素平方和的平方根
- 可类比L2范数
可利用低秩矩阵来近似单一数据矩阵.
用数学表示就是去找一个秩为k的矩阵B,使得矩阵B与原始数据矩阵A的差的F范数尽可能地小。
$ B = \mathop{argmin}_{rank(B)=k}{||A-B||_F}$
Lagrange Multiplier 和KKT条件
https://www.cnblogs.com/sddai/p/5728195.html
在求解最优化问题中,拉格朗日乘子法(Lagrange Multiplier)和KKT(Karush Kuhn Tucker)条件是两种最常用的方法。在有等式约束时使用拉格朗日乘子法,在有不等约束时使用KKT条件。
我们这里提到的最优化问题通常是指对于给定的某一函数,求其在指定作用域上的全局最小值(因为最小值与最大值可以很容易转化,即最大值问题可以转化成最小值问题)。提到KKT条件一般会附带的提一下拉格朗日乘子。二者均是求解最优化问题的方法,不同之处在于应用的情形不同。
一般情况下,最优化问题会碰到一下三种情况:####(1)无约束条件
这是最简单的情况,解决方法通常是函数对变量求导,令求导函数等于0的点可能是极值点。将结果带回原函数进行验证即可。
####(2)等式约束条件
设目标函数为f(x),约束条件为$h_k(x)$,形如:
s.t. 表示subject to ,“受限于”的意思,l表示有l个约束条件。
$$
minf(x)
s.t. h_k(x)=0 k=1,2,…l
$$
则解决方法是消元法或者拉格朗日法。消元法比较简单不在赘述,这里主要讲拉格朗日法,因为后面提到的KKT条件是对拉格朗日乘子法的一种泛化。
例如给定椭球:
求这个椭球的内接长方体的最大体积。这个问题实际上就是条件极值问题,即在条件 下,求的最大值。
当然这个问题实际可以先根据条件消去 z (消元法),然后带入转化为无条件极值问题来处理。但是有时候这样做很困难,甚至是做不到的,这时候就需要用拉格朗日乘数法了。
首先定义拉格朗日函数F(x):
( 其中λk是各个约束条件的待定系数。)
然后解变量的偏导方程:
......,如果有l个约束条件,就应该有l+1个方程。求出的方程组的解就可能是最优化值(高等数学中提到的极值),将结果带回原方程验证就可得到解。
回到上面的题目,通过拉格朗日乘数法将问题转化为
对求偏导得到
联立前面三个方程得到和,带入第四个方程解之
带入解得最大体积为:
至于为什么这么做可以求解最优化?维基百科上给出了一个比较好的直观解释。
举个二维最优化的例子:
min f(x,y)
s.t. g(x,y) = c
这里画出z=f(x,y)的等高线(函数登高线定义见百度百科):
绿线标出的是约束g(x,y)=c的点的轨迹。蓝线是f(x,y)的等高线。箭头表示斜率,和等高线的法线平行。从梯度的方向上来看,显然有d1>d2。绿色的线是约束,也就是说,只要正好落在这条绿线上的点才可能是满足要求的点。如果没有这条约束,f(x,y)的最小值应该会落在最小那圈等高线内部的某一点上。而现在加上了约束,最小值点应该在哪里呢?显然应该是在f(x,y)的等高线正好和约束线相切的位置,因为如果只是相交意味着肯定还存在其它的等高线在该条等高线的内部或者外部,使得新的等高线与目标函数的交点的值更大或者更小,只有到等高线与目标函数的曲线相切的时候,可能取得最优值。如果我们对约束也求梯度∇g(x,y),则其梯度如图中绿色箭头所示。很容易看出来,要想让目标函数f(x,y)的等高线和约束相切,则他们切点的梯度一定在一条直线上(f和g的斜率平行)。
也即在最优化解的时候:∇f(x,y)=λ(∇g(x,y)-C) (其中∇为梯度算子; 即:f(x)的梯度 = λ* g(x)的梯度,λ是常数,可以是任何非0实数,表示左右两边同向。)
即:▽[f(x,y)+λ(g(x,y)−c)]=0λ≠0那么拉格朗日函数: F(x,y)=f(x,y)+λ(g(x,y)−c) 在达到极值时与f(x,y)相等,因为F(x,y)达到极值时g(x,y)−c总等于零。
min( F(x,λ) )取得极小值时其导数为0,即▽f(x)+▽∑ni=λihi(x)=0,也就是说f(x)和h(x)的梯度共线。
简单的说,在F(x,λ)取得最优化解的时候,即F(x,λ)取极值(导数为0,▽[f(x,y)+λ(g(x,y)−c)]=0)的时候,f(x)与g(x) 梯度共线,此时就是在条件约束g(x)下,f(x)的最优化解。
####(3)不等式约束条件
设目标函数f(x),不等式约束为g(x),有的教程还会添加上等式约束条件h(x)。此时的约束优化问题描述如下:
则我们定义不等式约束下的拉格朗日函数L,则L表达式为:
其中f(x)是原目标函数,hj(x)是第j个等式约束条件,λj是对应的约束系数,gk是不等式约束,uk是对应的约束系数。常用的方法是KKT条件,同样地,把所有的不等式约束、等式约束和目标函数全部写为一个式子L(a, b, x)= f(x) + a*g(x)+b*h(x),
KKT条件是说最优值必须满足以下条件:
1)L(a, b, x)对x求导为零;
2)h(x) =0;
3)a*g(x) = 0;
求取这些等式之后就能得到候选最优值。其中第三个式子非常有趣,因为g(x)<=0,如果要满足这个等式,必须a=0或者g(x)=0. 这是SVM的很多重要性质的来源,如支持向量的概念。
接下来主要介绍KKT条件,推导及应用。详细推导过程如下: