二分类(Binary Classification)

一张图片作为输入, 如果识别这张图片为猫，则输出标签1作为结果；如果识别出不是猫，那么输出标签0作为结果。现在我们可以用字母 来y表示输出的结果标签.

为了保存一张图片，需要保存三个矩阵，它们分别对应图片中的红、绿、蓝三种颜色通道，如果你的图片大小为64x64像素，那么你就有三个规模为64x64的矩阵，分别对应图片中红、绿、蓝三种像素的强度值.

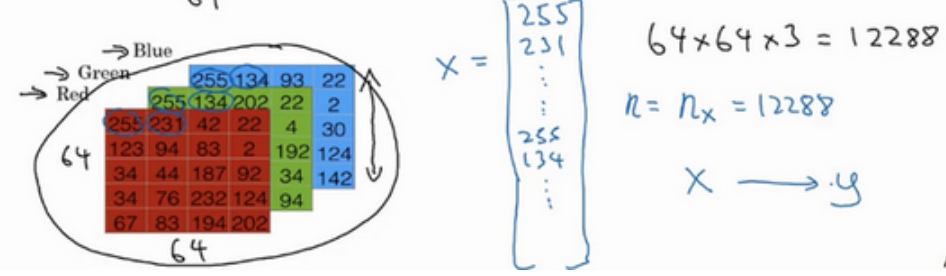
把这些像素值提取出来，然后放入一个特征向量x. 三个像素矩阵中像素的总量 = 64 * 64 * 3 所以 $n_x = 12288$ 表示向量的维度.

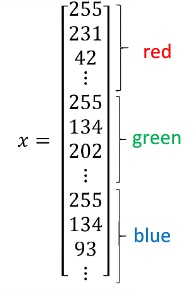
逻辑回归(Logistic Regression)

逻辑回归的Hypothesis Function（假设函数) $Given x, \tilde{y} = P(y=1 | x), where 0\le\tilde{y}\le1$ The parameter used in Logistic regression are:

• The input features vector: $x\in \textbf{R}^{n_x}$, where $n_x$ is the number of features
• The training label: $y\in0,1$
• The weights(特征权重): $w\in\textbf{R}^{n_x}$, where $n_x$ is the number of features
• The threshold: $b\in\textbf{R}$
• The output: $\tilde{y}=\theta(w^Tx+b)$ 让$\tilde{y}$表示实际值$y$等于1的机率的话, 应该在0到1之间, 而$w^Tx+b$可能比1要大得多, 或者甚至为一个负值, 所以输出$\tilde{y}$应该是等于由上面得到的线性函数式子作为自变量的sigmoid函数中
• Sigmoid function: $s = \theta(w^Tx+b) = \theta(z) = \frac{1}{1+e^{-z}}$ 关于$z$的sigmoid函数($\theta$()), 它是平滑地从0走向1(纵轴), 曲线与纵轴相交的截距是0.5.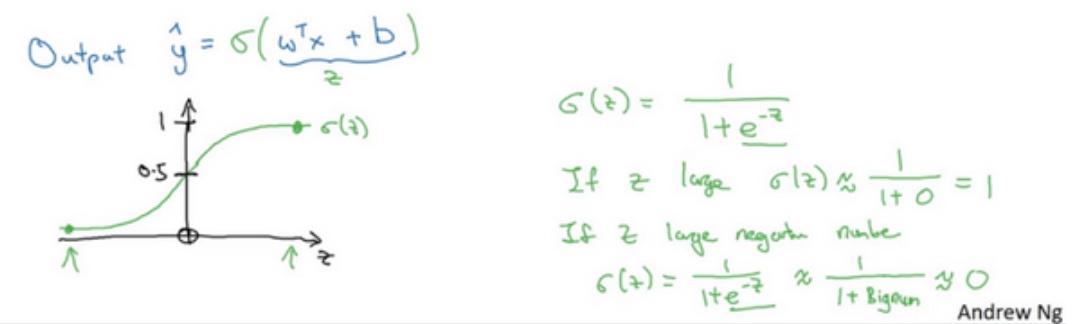

Some observation from graph:

• If z is a large positive number, then $\theta(z) = 1$
• If z is small or large negative number, then $\theta(z) = 0$
• If z = 0, then $\theta(z) = 0.5$

逻辑回归的代价函数（Logistic Regression Cost Function）

通过训练代价函数来得到参数w和参数b

Recap:

$\tilde{y}^{(i)}=\theta(w^Tx^{(i)}+b)$, where $\theta(z^{(i)}) = \frac{1}{1+e^{-z^{(i)}}}$ $Given \{(x^{(i)},y^{(i)}),...,(x^{(m)},y^{(m)})\}$, we want $\tilde{y}^{(i)}\approx {y}^{(i)}$

注: $x^{(i)}$ the i-th training example

Loss(error) function:

The loss function measures the discrepancy between the prediction($\tilde{y}$) and the desired output($y$). (Loss function computes the error for a single training example) (通过损失函数$L$，来衡量预测输出值和实际值有多接近. 损失函数只适用于单个训练样本, 而代价函数是参数的总代价)

$L(\tilde{y}^{(i)},{y}^{(i)})=\frac{1}{2}(\tilde{y}^{(i)}-{y}^{(i)})^2$

$L(\tilde{y}^{(i)},{y}^{(i)})=-(y^{(i)}log(\tilde{y}^{(i)})+(1-{y}^{(i)})log(1-\tilde{y}^{(i)}))$

(在最外面加一个负号是因为log(x), 当x<1时, log(x)都是负数)

• If $y^{(i)}=1: L(\tilde{y}^{(i)},{y}^{(i)})=-log(\tilde{y}^{(i)})$ where $log(\tilde{y}^{(i)})$ and $\tilde{y}^{(i)}$ should be close to 1 (如果想要损失函数$L$尽可能得小，那么$\tilde{y}$就要尽可能大，因为sigmoid函数取值[0,1]，所以$\tilde{y}$会无限接近于1)
• If $y^{(i)}=0: L(\tilde{y}^{(i)},{y}^{(i)})=-log(1-\tilde{y}^{(i)})$ where $log(1-\tilde{y}^{(i)})$ and $\tilde{y}^{(i)}$ should be close to 0 (如果想要损失函数$L$尽可能得小，那么$\tilde{y}$就要尽可能小，因为sigmoid函数取值[0,1]，所以$\tilde{y}$会无限接近于0)

(注: logistic的loss function又叫作cross entropy loss 交叉熵损失函数)

Cost function:

The cost function is the average of the loss function of the entire training set. We are going to find the parameter w and b that minimize the overall cost function. (找到合适的w和b，来让代价函数$J$ 的总代价降到最低)

$$ J(w,b) = \frac{1}{m} \sum^m_{i=1} L(\tilde{y}^{(i)},{y}^{(i)}) =-\frac{1}{m}\sum_{i=1}^m[y^{(i)}log(1-\tilde{y}^{(i)})+(1-{y}^{(i)})log(1-\tilde{y}^{(i)})]$$

梯度下降法（Gradient Descent）

梯度下降: 在测试集上, 通过最小化代价函数(成本函数)$J(w,b)$来训练的参数w和b.

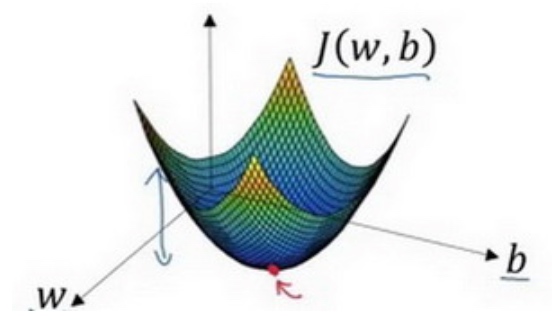
由于逻辑回归的代价函数(成本函数)$J(w,b)$特性，我们必须定义代价函数(成本函数)$J(w,b)$为凸函数(convex function) (非凸函数有很多不同的局部最小值)

假定代价函数（成本函数）$J(w)$ 只有一个参数w，即用一维曲线代替多维曲线

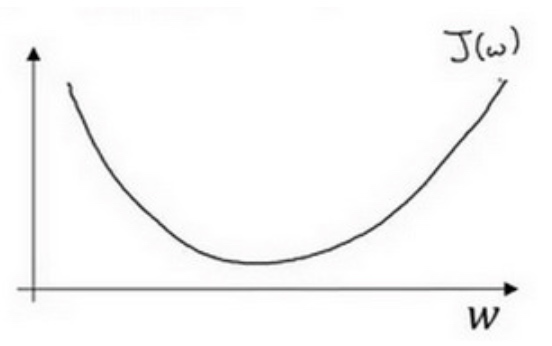
$$ Repeat \{ w:= w - \alpha\frac{dJ(w)}{dw} \} $$

$\alpha$表示学习率（learning rate), 用来控制步长（step), 即向下走一步的长度. $\frac{dJ(w)}{dw}$就是函数$J(w)$对$w$求导（derivative) (导数就是斜率（slope))

某点的导数就是这个点相切于$J(w)$的小三角形的高除宽.

逻辑回归的代价函数（成本函数)$J(w,b)$是含有两个参数的.

• $w:= w - \alpha\frac{\delta J(w,b)}{\delta w}$
• $b:= b - \alpha\frac{\delta J(w,b)}{\delta b}$

$\frac{\delta J(w,b)}{\delta w}$就是函数$J(w,b)$对$w$求偏导

注:

当函数只有一个参数时, 小写字母$d$用在求导数（derivative); 当函数含有两个以上的参数时, 偏导数符号$\delta$用在求导数（partial derivative);

导数(derivative)

计算图(Computation Graph)

一个神经网络的计算, 都是按照前向或反向传播过程组织的. 首先计算出一个新的网络的输出（前向过程), 紧接着进行一个反向传输操作, 用来计算出对应的梯度或导数.

(蓝色箭头是正向传播, 红色箭头是反向传播)

使用计算图求导数（Derivatives with a Computation Graph）

链式法则:

$\frac{dJ}{du}=\frac{dJ}{dv}\frac{dv}{du}$

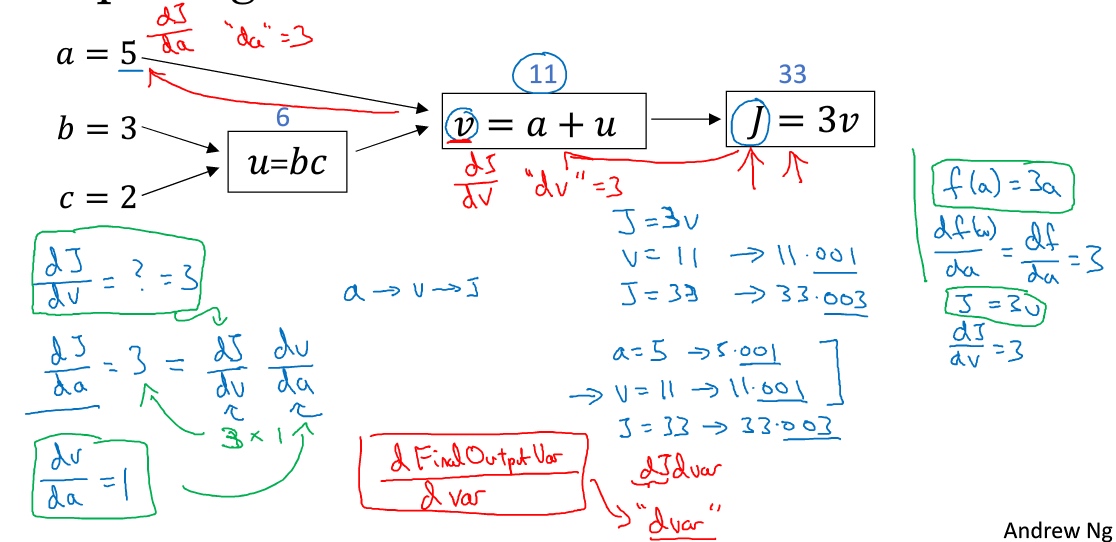
a增加了, v也会增加，增加多少取决于$\frac{dv}{da}$, 然后v的变化导致J也在增加, 这就是微积分里的链式法则

反向传播就是代价函数J对每个参数求导, 求导的结果即每个参数会对代价函数J的值产生的影响/变化, 再通过梯度下降对每个参数进行更新(参数 = 参数 - 步长 * 求导结果), 用更新的参数再进行正向传播, 反复此过程最终得到最小化的代价函数

逻辑回归中的梯度下降（Logistic Regression Gradient Descent）

假设样本只有两个特征x1和x2, 计算需要输入参数w1,w2和b, 除此之外还有特征值x1和x2. 因此的计算公式为: $z=w_1x_1+w_2x_2+b$

(a逻辑回归的输出，y是样本的标签值)

单个样本实例的反向传播和梯度下降:

1. 损失函数L对a求导, $da = \frac{dL(a,y)}{da} = -\frac{y}{a} + \frac{1-y}{1-a}$
2. 损失函数L对z求导, $dz = \frac{dL(a,y)}{dz} = \frac{dL}{da}\frac{da}{dz} = (-\frac{y}{a} + \frac{1-y}{1-a})(a(1-a)) = a-y$
   1. $\frac{da}{dz} = a(1-a)$ (对sigmoid函数求导)
   2. $\frac{1}{1+e^{-z}} = (1+e^{-z})^{-1} = -(1+e^{-z})^{-2}(-e^{-z}) = \frac{(1+e^{-z})-1}{(1+e^{-z})^2}=\frac{1}{1+e^{-z}} - \frac{1}{(1+e^{-z})^2} = \frac{1}{1+e^{-z}}(1-\frac{1}{1+e^{-z}})$
   3. since $a = \frac{1}{1+e^{-z}}$
   4. so $\frac{da}{dz} = a(1-a)$
3. 损失函数L对参数w1求导, $dw_1 = \frac{dL(a,y)}{dw_1} = \frac{dL}{da}\frac{da}{dz}\frac{dz}{dw_1} = x_1*dz = x_1(a-y)$
   1. $\frac{dz}{dw_1} = x_1$
4. 同理, 损失函数L对参数w2求导, $dw_2 = x_2(a-y)$
5. 同理, 损失函数L对参数b求导, $db = 1(a-y)$
6. 更新$w_1 = w_1 - \alpha dw_1$
7. 更新$w_2 = w_2 - \alpha dw_2$
8. 更新$b = b - \alpha db$

m 个样本的梯度下降(Gradient Descent on m Examples)

损失函数$J(w,b)=\frac{1}{m}\sum_{i=1}^mL(\tilde{y}^{(i)},{y}^{(i)})=-\frac{1}{m}\sum_{i=1}^m[y^{(i)}log(1-\tilde{y}^{(i)})+(1-{y}^{(i)})log(1-\tilde{y}^{(i)})]$

带有求和的全局代价函数，实际上是1到m项各个损失的平均. 所以它表明全局代价函数对w1的微分, 也同样是各项损失对w1微分的平均

J=0;dw1=0;dw2=0;db=0;
for i = 1 to m
    z(i) = wx(i)+b;  # 正向
    a(i) = sigmoid(z(i));  # 正向
    J += -[y(i)log(a(i))+(1-y(i)）log(1-a(i));  # lost function
    dz(i) = a(i)-y(i);  # 反向
    dw1 += x1(i)dz(i);  # 反向
    dw2 += x2(i)dz(i);  # 反向
    db += dz(i);  # 反向
J/= m;
dw1/= m;
dw2/= m;
db/= m;
w=w-alpha*dw
b=b-alpha*db

这种计算的缺点 - 两个for loop, 第一个for循环遍历所有m个训练样本, 第二个for循环遍历所有n个特征 (上述例子中只有2个特征x1,x2因此没使用for循环) 会导致computationally expensive

向量化可以摆脱这种for循环

向量化(Vectorization)

用向量化去取代代码中for循环. 例子 - 在逻辑回归中计算$z=w^Tx + b$ :

非向量化的实现:

z = 0
for i in range(n_x):
    z += w[i] * x[i]
z+=b

向量化实现:

z=np.dot(w,x)+b

时间对比:

import numpy as np #导入numpy库
a = np.array([1,2,3,4]) #创建一个数据a
print(a)
# [1 2 3 4]
import time #导入时间库
a = np.random.rand(1000000)
b = np.random.rand(1000000) #通过round随机得到两个一百万维度的数组
tic = time.time() #现在测量一下当前时间
#向量化的版本
c = np.dot(a,b)
toc = time.time()
print(“Vectorized version:” + str(1000*(toc-tic)) +”ms”) #打印一下向量化的版本的时间
​
#继续增加非向量化的版本
c = 0
tic = time.time()
for i in range(1000000):
    c += a[i]*b[i]
toc = time.time()
print(c)
print(“For loop:” + str(1000*(toc-tic)) + “ms”)#打印for循环的版本的时间

More example:

Logistic regression modification:

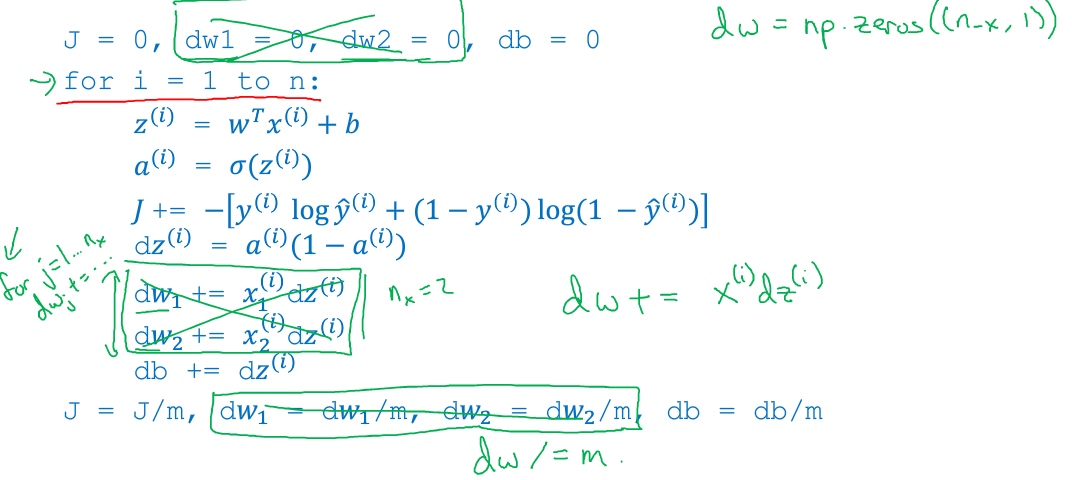
特征的for循环替代:

1. 初始化$dw_1=0, ...$ 用 $dw=np.zeros((n_x,1))$代替
2. $dw_1 += x^{(i)}_1dz^{(i)}, ...$ 用 $dw += x^{(i)}dz^{(i)}$代替
3. 最后, $dw_1=dw_1 / m, ...$ 用$dw = dw/m$代替

向量化逻辑回归的正向传播(Vectorizing Logistic Regression)

定义一个矩阵$X$作为训练输入 $X \in \textbf{R}^{n_x * m}$

• $n_x$是特征数量 (行)
• $m$是训练样本数量 (列)

特征权重矩阵 $w$, $w \in \textbf{R}^{n_x * 1}$, 所以$w^T \in \textbf{R}^{1*n_x}$

实数 $b$ 在python中会被自动扩展(广播)成一个$1 * m$的矩阵

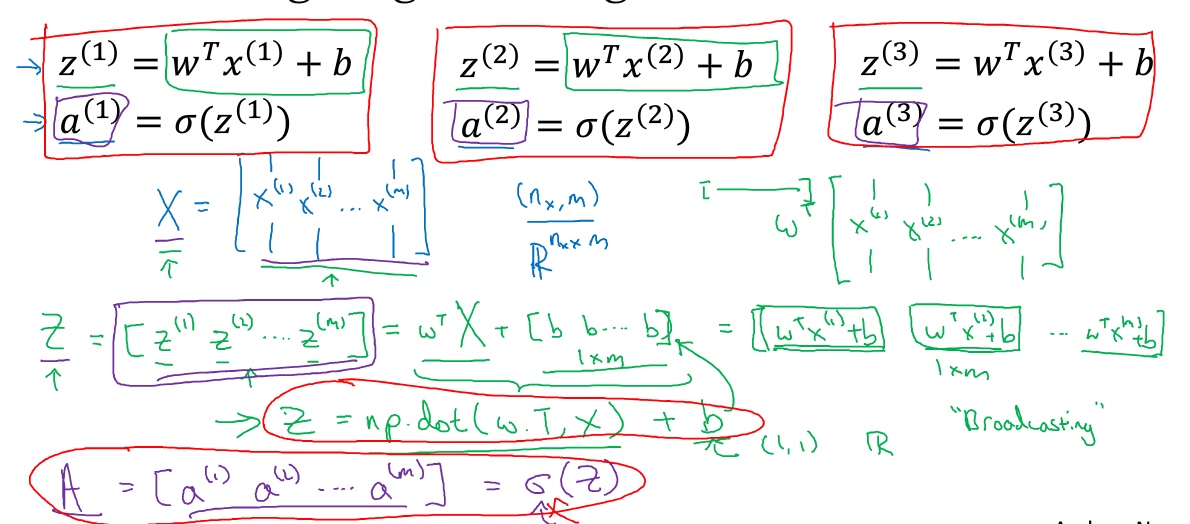
所以, 结果Z是一个$1 * m$的矩阵

Z = np.dot(w.T,X) + b

最终定义$A$来储存向量在sigmoid函数中计算的结果, $A = \theta(Z)$

这就是在同一时间内你如何完成一个所有m个训练样本的前向传播向量化计算.

向量化逻辑回归的梯度输出（Vectorizing Logistic Regression’s Gradient）

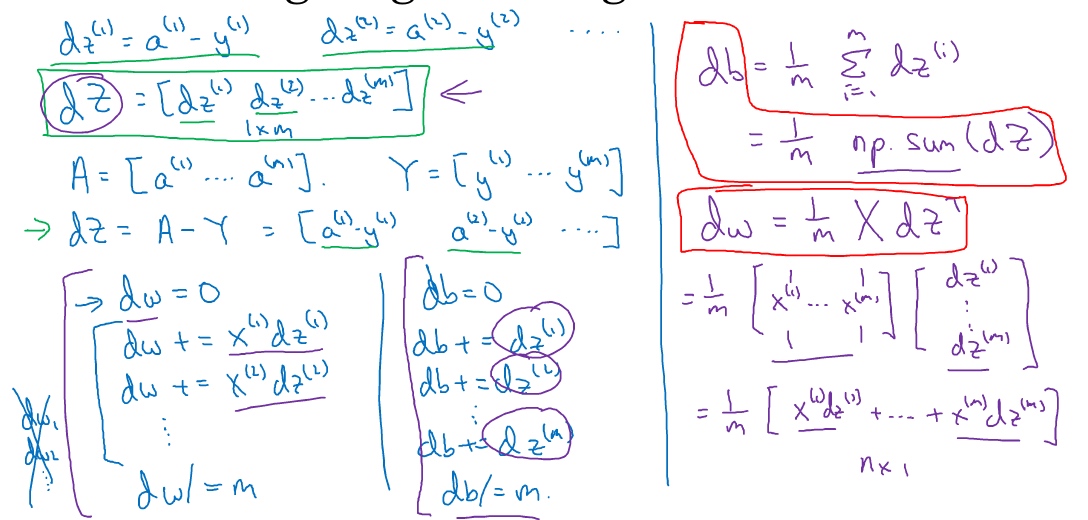
最终向量化的结果在下图右部:

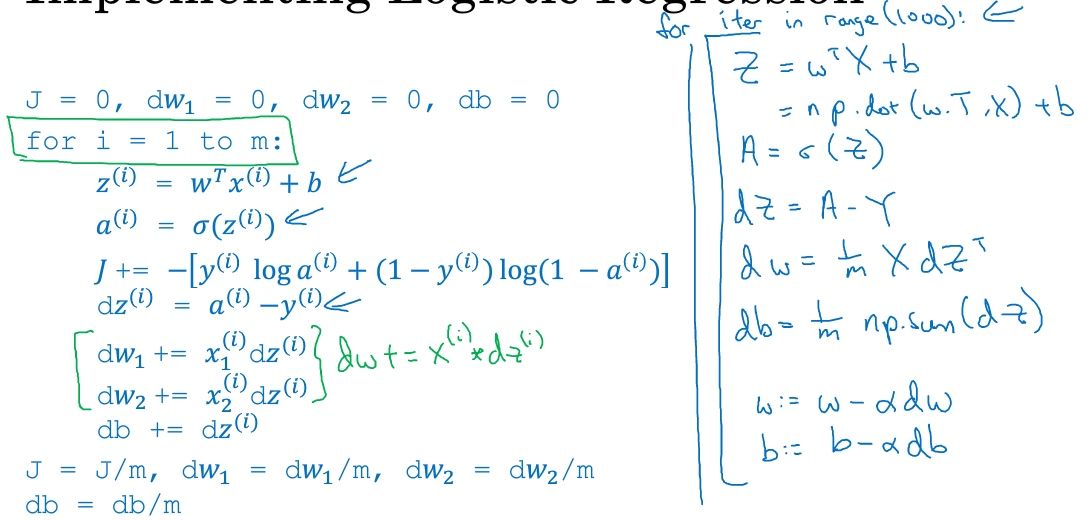
Python broadcasting & numpy vector

broadcasting

Python broadcasting 就是自动展开 auto-expanding

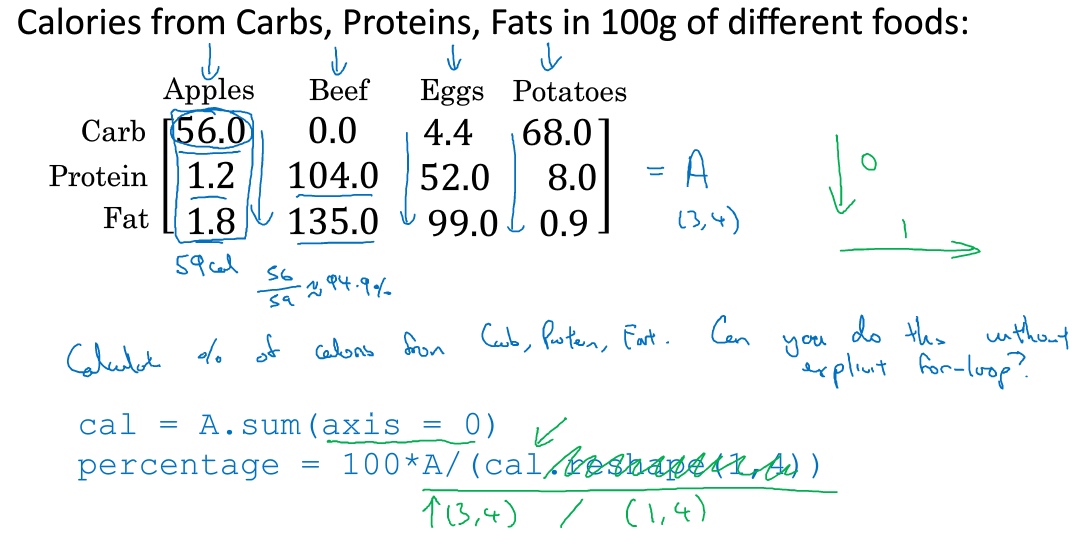
General Principle: numpy广播机制: 如果两个数组的后缘维度的轴长度相符或其中一方的轴长度为1，则认为它们是广播兼容的. 广播会在缺失维度和轴长度为1的维度上进行

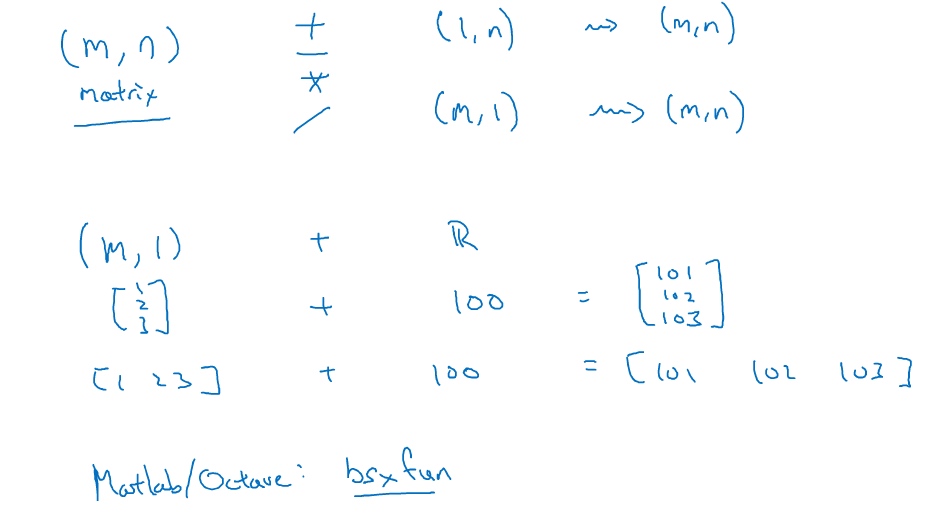
下面解释上图中的例子:

A note on python or numpy vectors

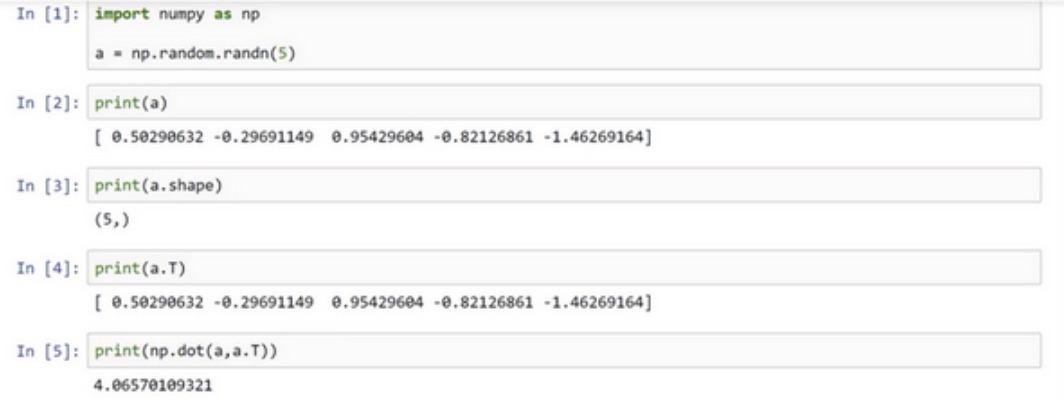
$a = np.random.rand(5)$

$a.shape$ 的结果是(5,)

输出a和a的转置的内积, 结果不是一个矩阵而是一个数

$a = np.random.rand(5,1)$

$a.shape$ 的结果是(5,1), 输出a和a的转置的内积, 结果是一个矩阵

conclusion:

• 别使用一维数组
• 使用column vector or row vector
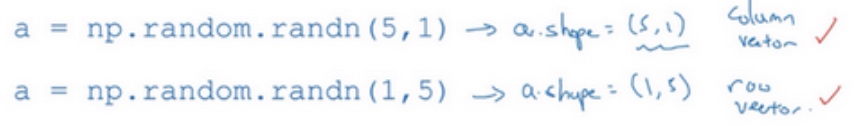
• 如果不完全确定一个向量的维度(dimension), 扔进一个断言语句(assertion statement)
• 如果不小心以一维数组来执行, 重新改变数组维数a.reshape(5,1)

logistic 损失函数的解释（Explanation of logistic regression cost function）

约定$\tilde{y} = p(y=1|x)$，即算法的输出$\tilde{y}$是给定训练样本$x$条件下$y$等于1的概率。换句话说，如果$y=1$，在给定训练样本$x$条件下$y=\tilde{y}$；反过来说，如果$y=0$，在给定训练样本$x$条件下$y$等于1减去$\tilde{y}(y=1-\tilde{y})$，因此，如果$\tilde{y}$代表$y=1$的概率，那么$1-\tilde{y}$就是$y=0$的概率。接下来，我们就来分析这两个条件概率公式

上述的两个条件概率公式可以合并成如下公式：

$p(y|x)=\tilde{y}^y(1-\tilde{y})^{(1-y)}$

• 当$y=1$时, $p(y|x)=\tilde{y}$
• 当$y=0$时, $p(y|x)=1-\tilde{y}$

由于 log 函数是严格单调递增的函数，最大化$log(p(y|x))$等价于最大化$p(y|x)$, 并且计算$p(y|x)$的 log对数，就是计算$log(\tilde{y}^y(1-\tilde{y})^{(1-y)})$ , 通过对数函数化简为：

$ylog\tilde{y} + (1-y)log(1-\tilde{y})$

前面提到的损失函数的负数$-L(\tilde{y},y)$，前面有一个负号的原因是当训练学习算法时需要算法输出值的概率是最大的（以最大的概率预测这个值），然而在逻辑回归中需要最小化损失函数，因此最小化损失函数与最大化条件概率的对数$log(p(y|x))$关联起来了，因此这就是单个训练样本的损失函数表达式.

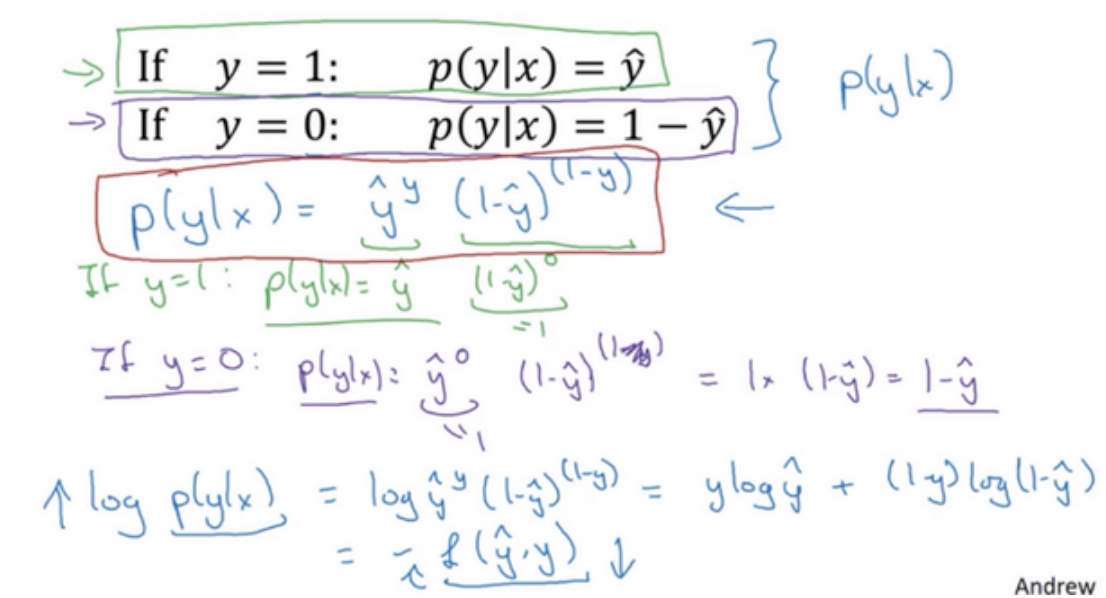
在m个训练样本的整个训练集的表示:

$P(labels\; in\; training\; set) = \prod_{i=1}^m P(y^{(i)} | x^{(i)})$

做最大似然估计(加log函数, 然后求导)，需要寻找一组参数，使得给定样本的观测值概率最大，但令这个概率最大化等价于令其对数最大化，在等式两边取对数：

$P(labels\; in\; training\; set) = log\prod_{i=1}^m P(y^{(i)} | x^{(i)}) = \prod_{i=1}^m logP(y^{(i)} | x^{(i)}) = \prod_{i=1}^m -L(\tilde{y}^{(i)},y^{(i)})$

使用最大似然估计(求出一组参数，使这个式子取最大值), 将负号移到求和符号的外面, 这样就推导出先前给出的逻辑回归的成本函数:

$J(w,b)=\prod_{i=1}^m L(\tilde{y}^{(i)},y^{(i)})$

由于训练模型时，目标是让成本函数最小化(不是最大化)，所以不是直接用最大似然概率，所以要去掉这里的负号，最后为了方便，可以对成本函数进行适当的缩放，我们就在前面加一个额外的常数因子$\frac{1}{m}$，即:

$J(w,b)=\frac{1}{m} \prod_{i=1}^m L(\tilde{y}^{(i)},y^{(i)})$

Conclusion:

为了最小化成本函数$J(w,b)$，从logistic回归模型的最大似然估计的角度出发，假设训练集中的样本都是独立同分布的条件下